Двойственная задача. Теневые цены

Для любой задачи линейного программирования можно сфор­мулировать задачу-двойник, или, иначе, двойственную задачу. Эта задача-двойник является своеобразным "зеркальным отражением" исходной задачи, поскольку ее формулировка использует те же параметры, что и исходная задача, а ее решение может быть получено одновременно с решением исходной задачи. Фактичес­ки при решении исходной задачи симплекс-методом одновремен­но решается и двойственная задача, и наоборот. Следует также заметить, что исходная и двойственная задачи совершенно сим­метричны. Если двойственную задачу рассматривать как исход­ную, то исходная будет для нее двойственной.

Одной из важнейших "зеркальных" связей между исходной и двойственной задачами является связь "переменные решения - те 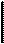невые цены ресурсов". Для того чтобы уловить эту связь, сфор­мулируем содержательно двойственную задачу к знакомой нам задаче об оптимальном плане выпуска продукции мебельного цеха.

Постановка двойственной задачи к задаче об оптимальном плане выпуска продукции мебельного цеха

Пусть имеется покупатель на все ресурсы, используемые для выпуска продукции мебельного цеха (ДСП, стекло и труд). Таблица параметров та же, что и для исходной задачи (таблица 10.3).

Какие цены на эти ресурсы нужно назначить, чтобы продать их было выгоднее, чем производить продукцию? Какую минимальную сумму можно выручить от продажи ресурсов при этом условии?

Таблица 10.3 - Параметры задачи

Ресурсы	Запасы	Продукты
Шкаф	Тумба
ДСП		3,5
Стекло
Труд
Прибыль

Поскольку в этой задаче три вида ресурсов, то переменных ре­шения, очевидно, должно быть тоже три. Это цены, которые на­значает производитель при продаже,

1 м ДСП - у₁,

1 м стекла - у₂,

1 дня труда рабочего цеха - у₃.

Сразу заметим, что эти цены называются теневыми. Они, разу­меется, не могут иметь никакого отношения к рыночным ценам
на данные ресурсы, поскольку, как будет видно из решения, ника­ких рыночных (или внерыночных) механизмов формирования цен
на данные ресурсы в решении не рассматривается.

Теневые цены характеризуют ценность ресурсов для произво­дителя.

Целевая функция - это, очевидно, прибыль, которую получит производитель - продавец ресурсов, если продаст по этим ценам нее имеющиеся ресурсы. Таким образом, целевая функция, запи­санная в таблице элементов модели, — это сумма произведений искомых цен у₁,у₂, у₃ на запасы имеющихся ресурсов, приведен­ных в соответствующем столбце таблицы параметров задачи. Ра­зумеется, интерес продавца ресурсов состоит в том, чтобы про­дать их подороже. Однако интерес покупателя в том, чтобы ку­пить подешевле.

Решение данной задачи позволит продавцу определить ниж­ние границы цен на ресурсы, которые он может назначить, чтобы прибыль от их продажи была не ниже, чем прибыль от производства товаров на основе этих ресурсов. Целевую функцию данной задачи можно также рассматривать как издержки покупателя ре­сурсов, которые необходимо минимизировать, приняв во внима­ние интересы производителя - продавца ресурсов.

Цель производителя - продавца ресурсов - найти минимальное значение суммарной выручки от продажи всех ресурсов при условии, что продать их было бы не менее выгодно, чем произво­дить из них продукцию.

Соответственно при записи ограничений в таблице элементов мидели (таблица 10.4) использован тот же принцип. Если производитель (продавец ресурсов) хочет продать 3,5 м ДСП, 1 м стекла и I день труда рабочего, то он должен получить не меньше, чем прибыль от производства одного шкафа (на который, согласно данным таблицы параметров, и идут все эти ресурсы). Аналогично если он хочет продать 1 м ДСП, 2 м стекла и 1 день труда рабочего, то он должен получить не меньше, чем прибыль от производства одной тумбы.

Таблица 10.4 – Элементы модели

Переменные решения	Целевая функция
у1 - цена1 м ДСП у2 - цена1 м стекла у3 – цена 1 дня труда рабочего цеха	С = 350 у1 + 240 у2 + 150 у3
Ограничения
3,5 у1 + 1 у2 + 1 у3 ≥ 200 1 у1 + 2 у2 + 1 у3 ≥ 100 у1, у2, у3 ≥ 0

Симметрия исходной и двойственной задач хорошо видна из сводной таблицы параметров и элементов решения этих двух задач (таблица 10.5).

Таблица 10.5 – Соответствие между исходной и двойственной задачами (оптимальный план выпуска продукции мебельного цеха)

Ресурсы	Запасы	Продукты	Теневые цены
Шкаф	Тумба
ДСП		3,5		у1
Стекло				у2
Труд				У3
Прибыль
Количество единиц каждого продукта	х1	х2
	Исходная задача	Двойственная задача
Переменные решения	х1, х2	у1, у2, у3
Целевая функция	Прибыль = 200х1 + 100х2 (максимум)	Издержки = 350у1 + 240у2 + 150у3 (минимум)
Ограничения	3,5х1 + х2 ≤ 350 х1 + 2х2 ≤ 240 х1 + х2 ≤ 150	3,5у1 + у2 + у3 ≥ 200 у1 +2у2 + у3 ≥ 100

Как видно из этой таблицы, в исходной задаче две переменные и три ограничения; в двойственной - наоборот: три
переменные и два ограничения. Исходная задача - это задача на
максимум прибыли производителя продуктов; двойственная - на
минимум издержек покупателя ресурсов.

Целевая функция исходной задачи формируется как сумма произведений строки переменных (количеств продуктов разного типа х₁, х₂)на строку прибылей от производства единицы каждого продукта; целевая функция двойственной задачи - как сумма произ­ведений столбца переменных (теневых цен ресурсов у₁, у₂, у₃) на столбец запасов этих ресурсов.

Аналогично ограничение на расход каждого из используемых ресурсов в исходной задаче формируется как сумма произведе­ний строки переменных (х₁, х₂)на расход данного ресурса при производстве единицы каждого продукта. Ограничение на выручку от продажи ресурсов, идущих на производство данного продукта в двойственной задаче, формируется как сумма произведений столбца переменных решений (у₁, у₂, у₃) на столбец расходов каждого из ис­пользуемых ресурсов на производство единицы данного продукта.

Эта симметрия проявляется и при сопоставлении более общих формулировок исходной и двойственной задач, когда п продуктов может быть произведено из т ресурсов.

Однако прежде чем обсуждать эти общие соотношения, решим сформулированную двойственную задачу к задаче об оптималь­ном плане выпуска продукции мебельного цеха с помощью MS-Еxcel и проанализируем результат.

Решение двойственной задачи об оптимальном плане выпуска продукции мебельного цеха с помощью MS-Excel

I. Организуйте данные так, как показано на рисунке 10.9 "Двойственная задача к задаче об оптимальном плане выпуска продукции мебельного цеха".

1. Формула в ячейке В13 для целевой функции означает:

С = 350у₁ + 240у₂ +150у₃.

2. Формула в ячейке D11 - это выражение для левой части первого ограничения 3,5у₁ + у₂ + у₃. Не забудьте сделать адреса ячеек, в которых содержатся переменные, абсолютными ($ перед буквенным обозначением столбца и номером ряда можно получить,
нажав на функциональную клавишу F4 на клавиатуре компьютера).

3. Протяните формулу в ячейке D11 на ячейку Е11.

Рисунке 10.9. Организация данных на листе MS-Excel для двойственной задачи к при­меру "Оптимальный план выпуска продукции мебельного цеха"

II. Вызовите "Поиск решения":

1. Целевая ячейка: В13 - Мин.

2. Изменяя ячейки: F4:F7.

4. He забудьте отметить в параметрах минимизации, что это линейная модель.

III. Решение двойственной задачи представлено на рисунке 10.10.

Обратите внимание, что цена ресурса "стекло" у₂ = 0. Поду­майте почему.

Рисунке 10.10. Результат решения на листе MS-Excel для двойственной задачи к примеру «Оптимальный план выпуска продукции мебельного цеха"

Дата добавления: 2015-08-21