Построение аксонометрической проекции окружности

Окружность в аксонометрии может быть построена при помощи сетки. В этом случае окружность делим на п равных частей (рис. 16, а). Строим сетку и вписываем эллипс (рис. 16, б).

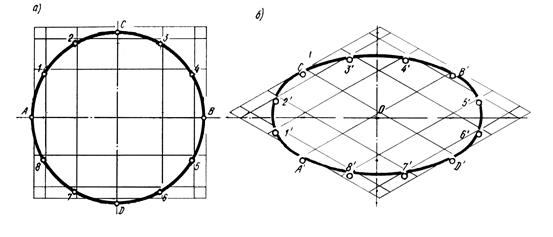
Рис. 16 а,б

Если известны сопряженные диаметры, которые строятся по аксонометрическим осям, то по ним можно найти и оси эллипса, используя для этого построение, данное на рис. 17,а. Например, окружность строится в косоугольной фронтальной изометрической проекции параллельно горизонтальной плоскости. Сопряженные диаметры А'₁В'₁ и С'₁D'₁ построены на аксонометрических осях Х' и У'.

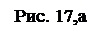
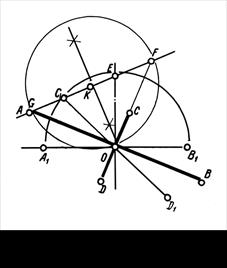В точке О' поставим перпендикуляр к одному из диаметров (например А'₁В'₁) и отложим на нем половину этого диаметра. Через полученную точку Е и конец второго диаметра – точку С'₁ проводим прямую. Разделив отрезок С'₁Е' пополам, из полученной точки К', как из центра, проводим окружность радиусом К'О' и отмечаем точки F' и G', в которых прямая С'₁Е' пересечется с окружностью. Прямая О'G' определит направление большей оси, а прямая О'F' – малой оси эллипса. Длина половины большой оси эллипса равна отрезкам G'Е' и F'С'₁, а длина половины малой оси эллипса – отрезком Е'F' и G'₁С'₁.

Эллипс можно построить и по сопряженным диаметрам другим способом (рис. 17,б). Два диаметра АВ и СD, каждый из которых делит пополам хорды, параллельные другому диаметру, называются сопряженными.

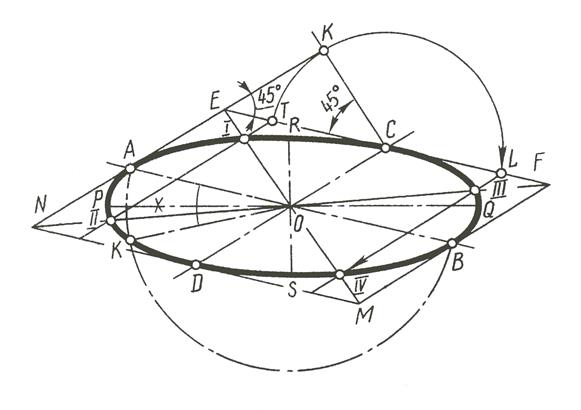
Рис. 17,б

На сопряженных диаметрах строят параллелограмм ЕFМN и проводят диагонали ЕМ и FN. На одной из полусторон параллелограмма, например ЕС, строят прямоугольный треугольник, катеты которого ЕК и СК направлены под углом 45⁰ к ЕС. Из точки С радиусом СК описывают полуокружность, пересекающую прямую ЕF в точках Т и L.

Через эти точки проводят прямые, параллельные коротким сторонам параллелограмма, и отмечают точки пересечения их с диагоналями ЕМ и FN. Получают точки I, II, III, IV, принадлежащие эллипсу. Эллипс определяется восемью точками – четыре на диагоналях и четыре (А,В,С,D) на сопряженных диаметрах. Этот прием применяют при построении эллипса по большой и малой осям. Зная размеры осей эллипса, можно построить его выше описанным способом (рис. 17,в).

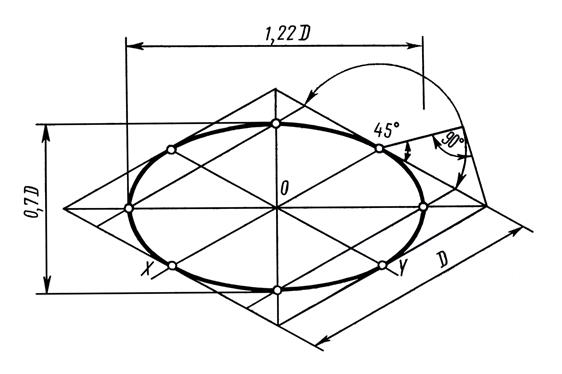
Рис. 17,в

Этот способ годится для всех видов аксонометрических проекций, где окружность проецируется с искажением. Этот же способ применяется и при построении окружности в перспективе.

Там, где это возможно, в аксонометрических проекциях эллипс заменяют овалом. Овал – это кривая, по очертанию похожая на эллипс, но строится она при помощи циркуля, что упрощает процесс построения.

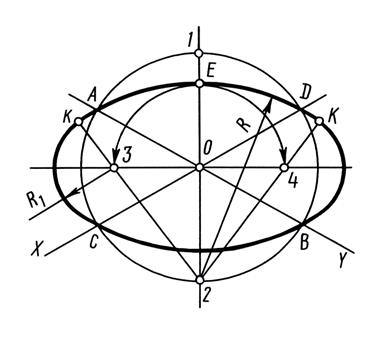
Рассмотрим способ построения овала, который применяется для любой аксонометрической проекции, с наибольшим приближением к эллипсу (рис.18,а).

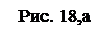На рис. 18,б дан пример построения овала, где по ортогональному чер-тежу окружности и вида аксонометрической про-екции, определена величина большой и малой осей эллипса, по которым построен овал,

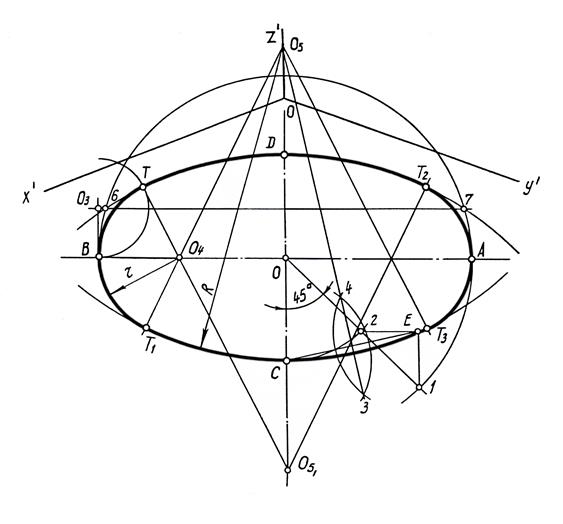
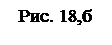приближенно заменяющий эллипс.

После того, как проведена большая АВ и малая СD оси, через точку О под углом 45⁰ к оси СD проведена прямая, которая в пересечении с окружностями R=ОС и R=ОА определяет точки 1 и 2. Вертикальная прямая, проведенная через точку 1, пересекается в точке Е с горизонтальной прямой, проведенной через точку 2. Точка Е принадлежит эллиптической кривой.

Прямая, проходящая через точки 3 и 4 и разделяющая отрезок СЕ пополам, в своем продолжении пересекает ось СD в точке О₅, которая является центром большой дуги овала с радиусом R = О₅С.

Для определения величины малого радиуса овала, через точку В проведена окружность радиусом R=ВО, которая пересекает дугу большого радиуса в двух точках 6 и 7.

Прямая, проходящая через точки 6 и 7, пересекает перпендикуляр, восстановленный из точки В к оси АВ в точке О₃, из которой радиусом О₃В проведена окружность до пересечения с дугой большого радиуса в точке Т, которая является точкой сопряжения большой и малой дуги овала. Прямая проведенная через точку Т и О₅, пересекает большую ось в точке О₄, которая является центром малой дуги.

Определив величину большого и малого радиуса овала и точки сопряжения этих дуг Т, Т₁, Т₂ и Т₃, при помощи циркуля строят овал, приближенно заменяющий эллипс.

На рис.19 в прямоугольной изометрической проекции дано построение многоугольника в различных положениях относительно плоскостей: а – общего положения; б – параллельно горизонтальной плоскости; в – параллельно профильной плоскости проекций.

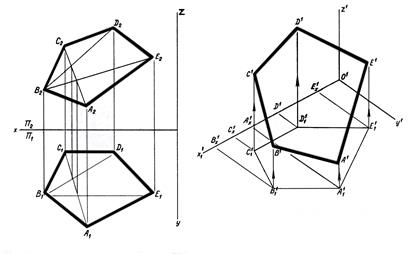
Рис. 19,а

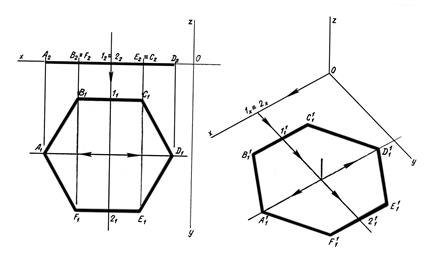
Рис. 19,б

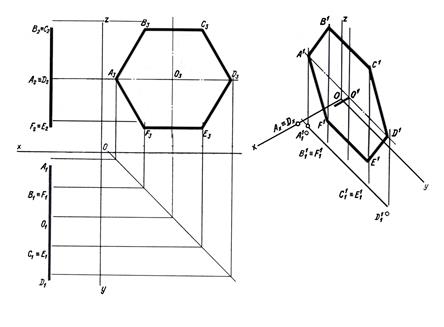
Рис. 19,в

Дата добавления: 2015-08-21