А Прямоугольная изометрия

Прямоугольная изометрическая проекция – наиболее простой вид прямоугольной аксонометрии. В прямоугольной изометрической проекции:

k_х = k_у = k_z = k, а поскольку φ = 90⁰, то 2 k² = 2, откуда k = √⅔ ≈ 0,82. Однако дробные коэффициенты искажения не удобны для практического применения, поэтому стандартом разрешается использовать, так называемые приведенные коэффициенты искажения k_х = k_у = k_z = 1, что дает так называемую приведенную изометрическую проекцию.

При использовании приведенных коэффициентов искажения аксонометрическое изображение пропорционально увеличивается в 1,22 раза по сравнению с оригиналом изображения. (1: 0,82 ≈ 1,22). Однако выигрыш за счет простоты построения оправдывает этот недостаток.

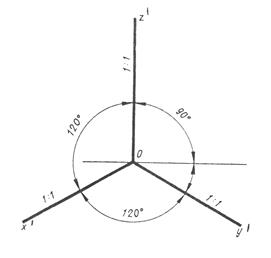
Поскольку коэффициенты искажения по всем осям одинаковые, то аксонометрическая плоскость проекций имеет одинаковый угол наклона ко всем осям (и плоскостям проекций) пространственной системы координат, откуда следует, что углы между аксонометрическими осями также одинаковы и равны 120⁰ (рис.6). При этом заметим, что ось z' для всех стандартных аксоно-метрических проекций распола-гается вертикально.

Из равенства коэффициентов искажения также следует, что параметры эллипсов и их ориентация относительно аксонометрических осей будут одинаковыми.

Установлено, что для приве-денной изометрической проекции значение большой оси эллипса 2а = 1,22D, малой – 2в = 0,71D (где D – диаметр окружности), рис. 7.

Большая ось эллипса всегда перпендикулярна одной из аксонометрических осей. А какой именно, зависит от положения в пространстве плоскости окружности до проецирования.

Рис. 7

Если плоскость окружности была перпендикулярна координатной оси Z, то большая ось эллипса будет перпендикулярна аксонометрической оси Z', если оси У, то У', если оси Х, то оси Х'.

Размеры осей эллипса для изометрической проекции можно определить графически (рис.8). Для этого проводим две взаимно перпендикулярные оси, чертим вокруг центра О окружность заданного диаметра.

Рис. 8

Из точек E и F делаем засечки радиусом EF, которые пересекаются в точках А и В. Соединяя точки А и В, получим большую ось эллипса, равную 1,22D, а соединяя точки E и F, получим малую ось равную 0,7D.

Дата добавления: 2015-08-21