Парная нелинейная корреляционаая связь. Корреляционное отношение.

При нелин корр. связи для получения оценки степени тесноты применяется η (корр отн-ние). Расчет этого пок-ля базируется на св-вах дисперсии, а именно на правиле сложения дисперсии.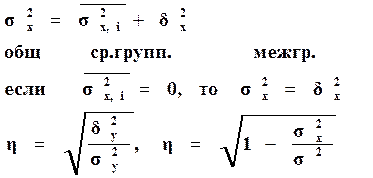

Коэф корреляции может принимать любое зн-ние между 0 и 1. 1-хар-ет функц. связь между признаками; 0 – отсутствие связи по рассм-мым данным. Хар-р связи выявляется в этом случае из анализа хар-ра изменения значения результатов признака с опр. направлением изменения зн-ния факторного признака. Если с увеличением зн-ния факт. признака обнаружена тенденция к снижению зн-ния результ. признака, то можно утверждать о наличии обратной связи между этими признаками. Если между признаками есть прямолинейная корр. связь, то величины коэфф-та парной (лин) корр-ции без учета знака и корр. отн-ний совпадают (=). Поэтому при изучении корр. связи предст. опр. интерес расчет как коэф-та r, так и корр. отнощения η, и сопоставление получ рез-в. Отличие в величинах r и η ук-ет на то, что расм-емая связь отличается от лин. формы при этом нужно иметь ввиду, что η >= |r|. Если квадрат разности 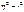не превышает 0,1 то утв-ся, возможным применять в кач-ве модели корр. связи ур-ния прямой. Для обоснования формы корр. связи (лин. или нелин) Есть более сложные методы. При практ. прим-нии для оценки степени тесноты связи корр. связи между признаками рассмотренные пок-лей r и η необх. помнить, что близость их к 1 или к 0 еще явл. док-вом того, что между данными признаками имеется или отсутствует связь. Эти результаты могли быть случ. совпадением или несовпадением изменчивости результир-го признака и изменением факт. признака. Факт наличия или отсутствия связи м. б. обоснован только теоритически сущностью рассм-х признаков. На практике для оценки корр. связи между признаками прим-ют такие стат. пок-ли, как квадраты пок-лей степени тесноты связи.

Эти коэф-ты наз-ся коэф-ми детерминации и хар-ют долю (%) изменчив-сти значений результативного признака, опр. влияние рассм-го факт призн

Дата добавления: 2015-08-21