Читайте также:
|
Предположим, что спрос 
за интервал времени 
является случайным и задан его закон распределения 
или плотность вероятностей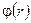 
(обычно функции и 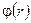оцениваются на основании опытных или статистических данных). Если спрос ниже уровня запаса 
, то приобретение (хранение, продажа) излишка продукта требует дополнительных затрат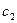 
на единицу продукта; наоборот, если спрос выше уровня запаса , то это приводит к штрафу за дефицит 
на единицу продукции.
В качестве функции суммарных затрат, являющейся в стохастических моделях случайной величиной, рассматривают ее среднее значение или математическое ожидание.
В рассматриваемой модели при дискретном случайном спросе , имеющем закон распределения , математическое ожидание суммарных затрат имеет вид:
. (6.14)
В выражении (6.14) первое слагаемое учитывает затраты на приобретение (хранение) излишка 
единиц продукта (при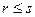 
), а второе слагаемое – штраф за дефицит на 
единиц продукта (при 
).
В случае непрерывного случайного спроса, задаваемого плотностью вероятностей 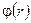, выражение 
принимает вид:
. (6.15)
Задача управления запасами состоит в отыскании такого запаса , при котором математическое ожидание суммарных затрат (6.14) или (6.15) принимает минимальное значение.
Можно доказать, что при дискретном случайном спросе выражение (6.14) минимально при запасе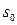 
, удовлетворяющем неравенствам
, (6.16)
а при непрерывном случайном спросе выражение (6.15) минимально при значении 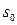, определяемом из уравнения
, (6.17)
где
есть функция распределения спроса , 
и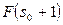 
– ее значения; 
плотность убытков из-за неудовлетворенного спроса, определяемая по формуле (6.12).
Дата добавления: 2015-08-21; просмотров: 174 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Статическая детерминированная модель с дефицитом | | | Модели управления запасами |