Понятие о комплексных частотных характеристиках(КЧХ). Амплитудно-частотоные характеристики(АЧХ), фазо-частотные характеристики(ФЧХ), годограф цепи.

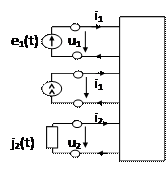Задача анализа электрической цепи была сформулирована ранее как задача определения реакции цепи на заданное внешнее воздействие. Вынесем из рассматриваемой цепи все ветви, содержащие независимые источники тока и напряжения, а также ветви, токи или напряжения которых подлежат определению. Оставшуюся часть цепи, содержащую идеализированные пассивные элементы и управляемые источники, представим в виде многополюсника

Зажимы (полюса), к кот. подкл. кажд. из независим.

источ., задающих внеш. воздействие на цепь, наз.

входными. зажимы, служащие для подкл. нагрузки, т.е ветви,

I или U кот. необход. опред., наз. выходными. Пара зажимов

наз. так же портом или стороной многополюсника.

Особенности:

1) ток, втекающий через один зажим порта, равен I, вытек.

вытекающему через другой зажим этого же порта;

2) между парами полюсов, принадлежащих к разным портам, не должно быть никаких внешних по отношению к многополиснику соединений (внутри многополюсника соединения, естественно могут быть).

Комплексной частотной характеристикой цепи называется отношение комплексных изображений отклика и воздействия:

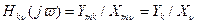, где Y_mk, Y_k — комплексные амплитуда и действующее значение реакции цепи; X_mk, X_k — комплексные амплитуда и действующее значение внешнего воздействия; k — номер выходных зажимов; v — номер входных зажимов.

В зависимости от того, какие величины (токи или напряжения) рассматриваются в качестве откликов и внешних воздействий, КЧХ. может иметь размерность сопротивления, проводимости или быть безразмерной.

КЧХ цепи численно равна комплексной амплитуде реакции цепи на внешнее воздействие с единичной амплитудой и нулевой начальной фазой.

Зависимости модуля Н_kv () и аргумента _kv () комплексной частотной характеристики от частоты со называются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками цепи.

Комплексную частотную характеристику можно изобразить и в виде одной зависимости— годографа КЧХ, построенного на комплексной плоскости. Годограф КЧХ представляет собой геометрическое место концов вектора H_kv(j), соответствующих изменению частоты от = 0 до 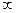 = . На годографе указываются точки, соответствующим некоторым значением частоты , и стрелкой показывают направление перемещения конца вектора H_kv(j) при увеличении частоты. КЧХ линейных цепей не зависят от амплитуды и начальной фазы внешнего воздействия, а определяются структурой цепи и параметрами входящих в нее элементов. Знание КЧХ позволяет определить реакцию цепи на заданное гармоническое воздействие.

Дата добавления: 2015-08-21