Імітаційне моделювання АСР, аналіз якості її функціонування й визначення запасів стійкості.

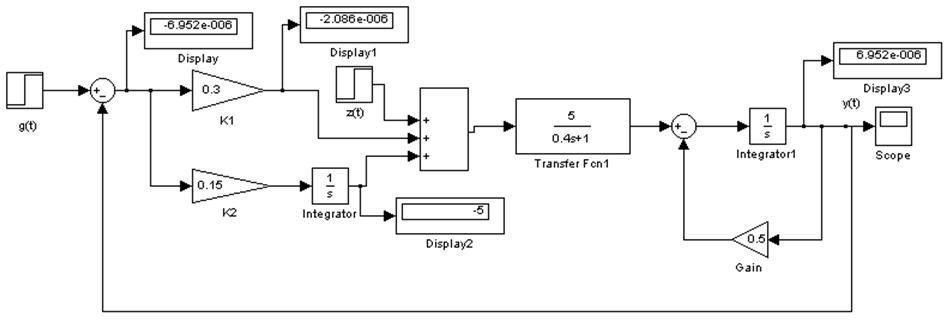
Імітаційна модель АСР наведена на рис. 6.

Ця модель відповідає структурній схемі, наведеній на рис. 5. В ній передбачений задатчик (блок step), що дозволяє сформувати завдання g(t), а також цифрові дисплеї (Display…Display4) для точного визначення сталих значень сигналів u₁(t), u₂(t), u₃(t) і y(t). Відзначимо, що сталі значення цих сигналів, отримані в результаті моделювання, збігаються з розрахунковими.

Крива перехідного процесу для вихідної величини наведена на рис. 7.

Знайдемо прямі оцінки якості:

· перерегулювання визначимо по формулі

 

    Рис. 6. Імітаційна модель АСР в Simulink

Рис. 7. Крива перехідного процесу для вихідний змінної

у досліджуваній АСР перерегулювання = 0%, тому що .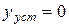

· час регулювання

· статичне відхилення

;

· число коливань

Таким чином, система забезпечує задані показники якості (перерегулювання).

Відзначимо, що при заданій структурі системи (регулятор має інтегральну складову) забезпечене Dy_ст = 0.

Визначимо запаси стійкості, скориставшись логарифмічними частотними характеристиками (ЛЧХ). Для цього в командному вікні MATLAB (рис. 8) потрібно задати функцію передачі АСР і далі для побудови ЛЧХ і запасів стійкості використати команду margin (W).

Команда grid on дозволяє включити сітку для кращого визначення значень по графіках.

Рис. 8. Командне вікно MATLAB

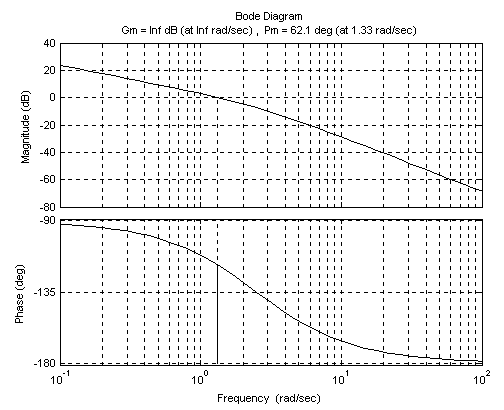
Результатом виконання вищевказаних команд буде графічне вікно (рис. 9) – Bode diagram: ЛАЧХ А(w) і ФЧХ j(w).

Отримані ЛЧХ наведені на рис. 9.

Рис. 9. Bode diagram: визначення запасів стійкості

Частота зрізу розімкнутої системи 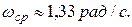Запас стійкості по фазі дорівнює Запас стійкості по модулі Такі запаси стійкості забезпечують достатнє віддалення системи від границі стійкості.

Запаси стійкості можуть бути оцінені й по асимптотичній ЛАЧХ.

Передатна функція розімкнутої системи (див. рис. 5)

Частота сполучання:

.

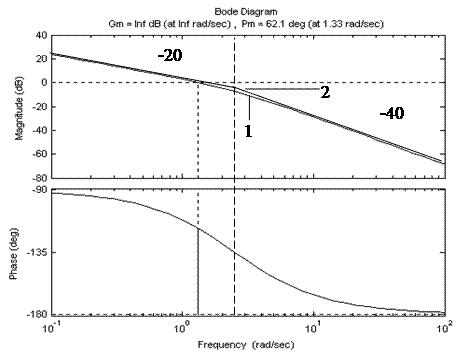
Побудова асимптотичної ЛАЧХ показана на рис. 10. З рисунка видно, що частота зрізу, знайдена по асимптотичній характеристиці, практично збігається з частотою зрізу на точній характеристиці. Значення зрушення фази визначили для частот 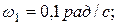і по формулі

Одержали:

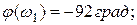
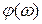За результатами розрахунку побудували графік у вигляді ламаної лінії (див. рис. 10).

Рис. 10. До визначення запасів стійкості:

1 - точна ЛАЧХ; 2 - асимптотична ЛАЧХ

Можна зробити висновок, що оцінити запаси стійкості з невеликою похибкою можна й по наближеним ЛЧХ.

Дата добавления: 2015-08-21