Читайте также:
|
Рассмотрим дифракцию плоских волн на длинной щели шириной b. Волновая поверхность падающей волны, плоскость щели и плоскость экрана параллельны друг другу. Дифракционная картина будет наблюдаться либо на экране, удаленном на бесконечность (на расстояние 
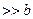), либо находящемся в фокальной плоскости линзы.
Воспользуемся задачей об интерференции света от N источников. Т.е., согласно принципу Гюйгенса-Френеля, волновую поверхность щели
мы заменим маленькими вторичными источниками световых волн числом N, причем 
. Расстояние между крайними источниками 
. Тогда 
, где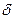 
- оптическая разность хода, 
- угол между горизонталью и пучками света.
.
Амплитуда в точке р определяется выражением 
из предыдущего параграфа:
А если , то 
и, разумеется, 
. Обозначим 
- разность хода между крайними точками:
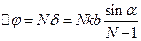
При , 
, и тогда 
. Тогда из выражения следует:
. 
Обозначим 
- амплитуда при 
. Запишем зависимость амплитуды от :
Теперь легко записать выражение для интенсивности:
Проанализируем формулу . Выясним условие минимума интенсивности:
, но 
, т.е.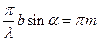 
, 
.
- условие минимума.
Количество минимумов не может быть бесконечно! Это количество можно определить из условия: 
, 
- целая часть, т.к. m должно быть целым; при 
минимумов вообще не будет, и интенсивность монотонно
убывает от середины к краям.
Наконец, построим график 
, иллюстрирующий выражение .
Дата добавления: 2015-08-21; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Условие минимумов. | | | Принципы работы лазера и свойства лазерного излучения |