Читайте также:
|
Условие главных максимумов.
Воспользуемся методом векторных диаграмм. Максимум будет наблюдаться тогда, когда векторы волн будут расположены вдоль одной линии, т.е.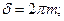 
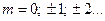В этом случае 
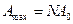, интенсивность 
.
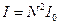Условие минимумов.
Минимум интенсивности – когда ломаная линия замкнется; при этом центральный угол будет равен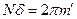 
, где 
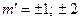…, но ни в коем случае не 0!
Отсюда следует, что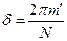 
, а если 
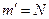или 
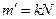, то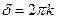 
- максимум! Тогда получаем уточненное условие для 
:
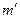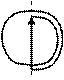
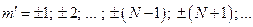
В промежутке между двумя главными максимумами находится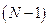 
минимумов, а следовательно 
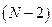вторичных максимумов. Изобразим зависимость интенсивности от 
для случая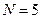 
(см. рисунок). Для первого вторичного максимума показано его положение на векторной диаграмме.
Найдем отношение между главными и вторичными максимумами:
,
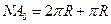где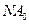 
- длина спирали, 
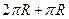- угол, умноженный на радиус.
Отсюда выражаем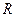 
:
,
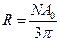тогда амплитуда первого вторичного максимума:
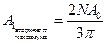
Найдем теперь отношение интенсивностей главного и вторичного максимумов:
,
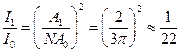для второго вторичного максимума аналогично получим: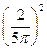 
.
Дата добавления: 2015-08-21; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модель фотонного газу Бозе — Ейнштейна | | | Дифракция Фраунгофера на щели. |