Дифракция Фраунгофера на двух щелях.

Лабораторная работа №10

Составители: Шелкунова З.В.

Базарсадаев Б.Ц.

Цыренжапов Б.Б.

Улан-Удэ

Лабораторная работа

Дифракция Фраунгофера на двух щелях.

Цель: Изучение дифракции на двух щелях.

Теория: Пусть плоская монохроматическая волна Ее^i(ωt-kx) падает перпендикулярно на щель ширины b в бесконечном непрозрачном экране.

Рис. 1. Схема наблюдения прохождения плоской волны через щель в непрозрачном экране.

Согласно геометрической оптике на любом расстоянии Z от экрана в плоскости регистрации Р должен наблюдаться «отпечаток», ширина которого D. В действительности, плоская волна, ограниченная по одному из направлений, вследствие соотношения неопределенности, получает разброс в поперечном волновом числе.

Δк_хD ≈ π

Отсюда следует; что волна за щелью становится расходящейся с характерным углом расходимости:

Θ ≈ ≈ ,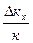

где λ – длина волны света, k - волновое число.

Волновое число это параметр, который характеризует колебания в пространстве, аналогично тому, как частота характеризует колебания во времени.

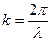
Расходимость прошедшего щель излучения, приводит к искажению распределения освещенности в плоскости Р от картины, следующей из геометрической оптики, причем эти искажения нарастают по мере удаления от Р от щели.

Такое явление, вызванное волновой природой света называется дифракцией.

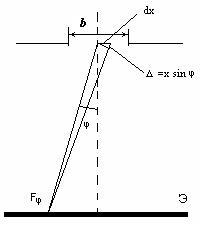Разобьем открытую волновую поверхность на элементарные зоны dx.

По принципу Гюйгенса-Френеля каждая точка фронта волны становится источником вторичных волн. Вторичные волны, от зон посылаемые в направлении определяемым φ соберутся в некоторой точке F_φ.

Амплитуда колебаний возбуждаемого зоной с шириной dx:

dA = Cdx, C – const.

A₀ =

dA = 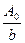dx

Каждая элементарная зона создает в т. F_φ колебание dE. Разность фаз между колебаниями с возбуждаемых в т. F_φ зонами с координатами 0 и x_i Þ Δ = xsinφ.

Тогда, колебание, возбуждаемое в F_φ элементарной зоной с координатами х:

Учитывая следующие обозначения получим:

(1)

Рассмотрим две щели шириной b и отстоящих друг от друга на a. Для получения дифракционной картины рассмотрим сначала одиночную щель, смещенную относительно начала координат на расстояние a в положительную сторону на оси x. Аналогично выражению (1) для смещенной щели получится выражение:

Дополнительный множитель не сказывается на распределении освещенности, однако, при сложении напряженностей полей от двух щелей разделенных на a, из-за множителя возникает интерференционный член, который добавляет дополнительные минимумы и максимумы на дифракционной картине Фраунгофера от одной щели.

С учетом следующих правил:

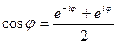
Выражение для интенсивности запишется в следующем виде:

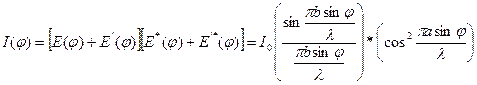(2)

Первый множитель = 0 в точках

bsinφ = ±kλ (k = 1, 2, 3, ……) (3)

- условие основного минимума.

Второй множитель принимает максимальное значение при условии

asinφ = ± k′λ (k′ = 1, 2, 3, ……) (4)

- условие, определяющее положение главных максимумов. Для этих направлений φ колебания от отдельных щелей взаимно усиливают друг друга.

Распределение интенсивности света в зоне Фраунгофера для двойной щели при a = 3b представлена на рис.3.

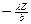
0

Рис.3. Картина дифракции на двух щелях шириной b разделенных расстоянием a = 3b.

Дата добавления: 2015-08-21