Дифракция Френеля на небольшом круглом диске

Вид дифракционной картины можно выяснить, пользуясь методом зон Френеля (рис.3). Сферическая волна, распространяющаяся от точечного источника S₀, встречает на своем пути диск диаметром d. Дифракционную картину рассчитываем на экране в точке М, лежащей на линии, соединяющей источник S₀ с центром диска. В данном случае закрытый диском участок волнового фронта S надо исключить из рассмотрения, т.к. по принципу Гюйгенса-Френеля закрытые участки не излучают. Зоны Френеля следует строить, начиная с краев диска. Если диск закрывает m первых зон Френеля, тогда амплитуда результирующего колебания в точке М равна

или

,

т.к. выражения в скобках равны нулю. Следовательно, в точке М всегда наблюдается интерференционный максимум (светлое пятно, называемое пятном Пуассона), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

Рис.3. Метод зон Френеля для расчета дифракционной картины на круглом непрозрачном диске

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки М, увеличивается угол φ_m. В результате интенсивность центрального максимума уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место слабая дифракционная картина. При освещении малого диска белым светом в центре на экране наблюдается белое пятно, окруженное системой концентрических цветных колец.

Дифракция Фраунгофера на небольшом круглом отверстии

и круглом диске

Метод Френеля эффективен лишь тогда, когда размер неоднородности (отверстие, диск, щель) сравним с размером зоны Френеля: d ~ , где d – размер тела, на котором происходит дифракция; l – расстояние до точки наблюдения. В этом случае происходит дифракция в сходящихся лучах, и небольшое число зон, на которые разбивается сферическая волна в отверстии, определяет дифракционную картину. Если отверстие в экране меньше зоны Френеля d , как, например, при очень удаленных от диафрагмы наблюдателя и источника света, то можно пренебречь кривизной фронта волны, считать ее плоской и картину дифракции характеризовать угловым распределением интенсивности потока. При этом падающий параллельный пучок света на отверстии становится расходящимся с углом расходимости 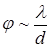. Математически корректная теория дифракции света на телах требует решения сложных граничных задач рассеяния электромагнитных волн, имеющих решения лишь для частных случаев. При выполнении расчета дифракции Фраунгофера на отверстии и диске задача приводится к бесселевым функциям. Максимумы и минимумы располагаются в виде концентрических колец и угловой радиус темных колец определяется приближенно соотношением

,

где r – радиус отверстия и m =1,2,….

Таким образом, чем больше радиус отверстия, тем мельче дифракционная картина. Интенсивности светлых колец очень малы по сравнению с интенсивностью центрального максимума (например, I₁ =0,018 I₀) и быстро убывают с увеличением порядка максимума.

Дифракция плоской волны при прохождении через круглое отверстие представляет большой практический интерес, т.к. с этим типом дифракции приходится иметь дело в различных оптических приборах, в которых роль отверстия играют оправы объективов. Еще один способ использования дифракции Фраунгофера – определение размера мелких частиц – изучается в настоящей лабораторной работе.

Дата добавления: 2015-08-21