Теоретическое введение

Дифракция света

Дифракцией называется совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью (например, при прохождении через отверстия в экранах, вблизи границ непрозрачных тел и т.п.).

В более узком смысле под дифракцией света понимают огибание светом встречных препятствий, т.е. отклонение от законов геометрической оптики.

Решающую роль в утверждении волновой теории света и её развитии, позволившем объяснить дифракцию света и дать методы её количественного расчета, сыграл Френель. Он показал, что закон прямолинейного распространения света является приближенным.

Френель использовал принцип Гюйгенса, согласно которому каждая точка поверхности S(t), до которой доходит волна в момент времени t, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта S(t+Δt) в следующий момент времени. При этом считается, что в однородной среде вторичные волны излучаются только вперед, в однородной изотропной среде вторичные волны – сферические (рис.1).

Принцип Гюйгенса решает задачу о направлении распространения волнового фронта, но не указывает способа расчета амплитуды волны, а, следовательно, и интенсивности волны, огибающей вторичные волны.

Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей о когерентности вторичных волн и их интерференции при наложении.

Согласно принципу Гюйгенса-Френеля:

1) световая волна, возбужденная каким-либо источником S₀, может быть представлена как результат суперпозиции системы вторичных источников – малых участков dS любой замкнутой вспомогательной поверхности S, проведенной так, чтобы она охватывала источник S₀ и не охватывала рассматриваемую точку M;

2) вторичные источники когерентны первичному и между собой, поэтому возбуждаемые ими вторичные волны интерферируют при наложении. Обычно в качестве поверхности S выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно;

3) амплитуда колебаний, возбуждаемых в точке М вторичным источником, пропорциональна отношению площади dS участка волновой поверхности S к расстоянию r от него до точки М и зависит от угла φ между внешней нормалью к волновой поверхности и направлением от элемента dS в точку М;

4) если часть поверхности S занята непрозрачными экранами, то закрытые вторичные источники не излучают, а остальные излучают так же, как и в отсутствии экранов.

Рис.1. Принцип Гюйгенса, позволяющий найти положение волнового фронта S(t+Δt) как поверхность, огибающую вторичные волны

Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства. В общем случае расчет интерференции вторичных волн сложный, однако в некоторых случаях нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием. Такой прием называется методом зон Френеля.

Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде от точечного источника S₀ (рис.2). Согласно принципу Гюйгенса-Френеля заменим действие источника S₀ действием вторичных источников, расположенных на вспомогательной поверхности S, являющейся поверхностью фронта волны. Разобьем волновую поверхность S на кольцевые зоны таким образом, чтобы расстояния от краев зоны до точки М отличались на λ/2. Это можно выполнить, проведя с центром в точке М сферы радиусами , , ... Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на λ/2, то в точку М они приходят в противоположной фазе, и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего колебания в точке М:

А= А₁ – А₂ + А₃ – А₄ + …,

где A₁, A₂, … – амплитуды колебаний, возбуждаемых соответствующими зонами.

При не слишком большом количестве зон m площади зон Френеля одинаковы, т.е. построение зон Френеля разбивает поверхность сферической волны на равные зоны.

Рис.2. Метод зон Френеля

Действия отдельных зон в точке М тем меньше, чем больше угол между нормалью к поверхности зоны n и направлением на М, т.е. действие зон постепенно убывает от центральной к периферическим. Кроме того, интенсивность излучения в направлении точки М уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки М. Учитывая оба фактора, можно записать:

А₁ > А₂ > А₃ > А₄ > ….

Приближенно можно считать, что амплитуда колебания A_m от некоторой зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон:

.

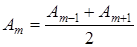Тогда результирующая амплитуда

.

Так как общее число зон Френеля, умещающихся на полусфере, очень велико (~10⁵), то оставшаяся часть от амплитуды последней зоны ничтожно мала, поэтому амплитуда результирующих колебаний определяется как бы действием половины центральной зоны Френеля.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально при использовании зонных пластинок, состоящих из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля. Если поместить такую пластинку в определенном месте, то она увеличивает освещенность в точке М.

Различают два случая дифракции света: дифракцию Френеля, или дифракцию в сходящихся лучах, и дифракцию Фраунгофера, или дифракцию в параллельных лучах. В первом случае на препятствие падает сферическая волна, а дифракционная картина наблюдается на экране, находящемся за препятствием на конечном расстоянии от него. Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути света, прошедшего через препятствие.

Дата добавления: 2015-08-21