Использование частотных распределений

Для того чтобы понять, насколько различаются усло­вия, мы можем нанести частотные распределения для этих условий на один и тот же график. Сравнение ста­новится более понятным, если не только отмечать вы­соту колонок, но соединить их вершины линией. (Это называется полигоном частот.) Данный метод уже был показан на рис. 4.3 для эксперимента по обучению испанскому языку.

По значительному перекрытию распределений мы можем судить, что тестовые оценки для двух условий — письменного и устного — различались незначительно.

Рассмотрим теперь распределения для эксперимен­та по измерению времени реакции, описанного в стати­стическом приложении к главе 1. Они показаны на рис. 4.4. Напомним, что это вымышленные данные. Предположим теперь, что они были получены в меж­групповом эксперименте. Тогда каждый из показателей времени реакции представляет среднее для одного из 184испытуемых, где 17 испытуемым предъявлялось данное условие. Этот пример может быть с тем же успехом представлен в терминах интраиндивидуального экспери­мента, как он первоначально излагался. Рассмотрение эксперимента как межгруппового мы делаем только для того, чтобы связать наш анализ с тематикой дан­ной главы.

Видно, что в данном случае различия между усло­виями более отчетливы, чем в эксперименте с испан­ским языком, т. е. перекрытие между распределениями меньше. Было бы хорошо иметь количественную меру различия вместо таких неопределенных терминов, как «кажется», «очевидно» и т. д. Такая количественная мера давала бы информацию, насколько сильна связь между независимой и зависимой переменными.

ВЫЧИСЛЕНИЕ ω²

Мы можем получить численную величину силы связи, вычислив ω² (ω — малая греческая буква омега; мы 185называем ω² омегой в квадрате). По существу, ω² — один из параметров генеральной совокупности, о кото­рых рассказывалось в статистическом приложении к главе 1. Его полное описание можно найти в работе Хейса (1973).

Рис. 4.4.Частотное распределение средних значений времени реак­ции на световой (условие А) и звуковой (условие Б) сигналы. Ось абсцисс — средние значения времени реакции (в мс). ось орди­нат — частота. Сплошная линия — световой сигнал, пунктирная — звуковой	Рис. 4.5.Объединенное частотное распределение средних значений Семени реакции. Ось абсцисс — средние значения времени реакции (в мс). Ось ординат — частота

Наше вычисление с использованием данных по вы­борке испытуемых дает оценку ω². Мы будем называть ее est ω².

Давайте построим новый график результатов экспе­римента по измерению времени реакции. Однако теперь мы не будем делать различий между тем, какое из двух условий — А (свет) или Б (тон) —было использовано. Как видно на рис. 4.5, это комбинированное распреде­ление несколько более растянуто, чем каждое из отдель­ных распределений для света и тона. Чем больше ис­ходные распределения отличаются друг от друга, тем больше будет растянуто комбинированное распределе­ние.

Если бы мы смогли провести бесконечный экспери­мент и при этом получили бы распределения, показан­ные на рис. 4.4 и 4.5, мы могли бы вычислить ω² прямо 186из параметра σ̅² _X следующим образом:

(4.1)

Однако поскольку наши данные получены только по одной выборке испытуемых, а не в бесконечном экспе­рименте, мы должны оценивать ω² по статистике S²_X:

(4.2)

Квадрат стандартного отклонения распределения на­зывается дисперсией.

Числитель этой формулы дает разность между дис­персиями комбинированного распределения и отдельно­го распределения, в нашем случае любого из условий А или Б. Делением этой разности на дисперсию ком­бинированного распределения мы придаем ей форму пропорции. Она отвечает на вопрос, на какую часть уменьшается дисперсия показателей при переходе от комбинированного распределения к отдельному.

Производя вычисления, нет необходимости сначала вычислять S_X и затем возводить его в квадрат, чтобы получить S²_X. Вспомните (из формулы 2.2):

Поэтому

(4.3)

В статистическом приложении к главе 3 мы вычис­лили ∑ х² для условия А (свет) и условия Б (тон):

Используем эти величины для нахождения S²_отд. Согласно Хейсу (с. 418), среднее по S²_A и S²_Б дает 187величину S²_отд при допущении равенства «истинных» дисперсий двух наборов:

(4.4)

поэтому

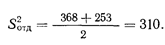
Такое же вычисление производится для комбиниро­ванного распределения:

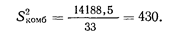
Подставляя эти величины в формулу 4.2, получаем

Это показывает сильную связь между независимой и зависимой переменными. Даже значение 0,20 уже до­статочно существенно. Значение никогда не может пре­высить 1; однако эта величина достигается редко. В то же время вычисление для эксперимента с испанским ЯЗЫКОМ дает

Это очень слабая связь между независимой и зави­симой переменными.

ПРИМЕНЕНИЯ ω²

Обратите внимание, что для S² _отд необходимо до­пускать равенство истинных дисперсий для двух усло­вий. В эксперименте по измерению времени реакции это допущение было приемлемым, поскольку дисперсии 188для двух условий довольно близки по величине. Это справедливо и для эксперимента с испанским языком. Однако для эксперимента с информацией о ценах (см. табл. 4.1) условие В давало значительно меньшее стандартное отклонение (особенно для времени выбора покупки), чем другие условия. Три дисперсии (квадра­ты стандартных отклонений) были равны 100, 92 и 1,2 для условий А, Б и В. При столь значительном разли­чии прямого способа вычисления ω2 нет. И здесь дело не в том, что число условий равно трем, а не двум. Если значения дисперсии близки, то величина ω² может быть вычислена для любого числа условий с использо­ванием S² _отд как среднего значения для всех условий. Приводившаяся процедура вычисления ω² может быть использована как для интраиндивидуальных, так и для межгрупповых данных. Дисперсия — это то, что отно­сится к пробам, а не к испытуемым.

ИНТЕРПРЕТАЦИЯ ω²

Мы можем рассматривать ω² как индикатор величины, на которую уменьшается неопределенность за счет то­го, что нам известно экспериментальное условие. В экс­перименте по измерению времени реакции мы кое-что знаем о среднем показателе для каждого отдельного испытуемого благодаря тому, что знаем эксперимен­тальное условие. Но в пределах каждого условия по­казатели варьируют, т.е. как-то распределены. Наша неопределенность измеряется дисперсией этого распре­деления. Если мы не знаем условия, предъявлявшегося испытуемому, наша неопределенность увеличивается: дисперсия комбинированного распределения больше, чем дисперсия для отдельного условия.

Таким образом, зная, какое из условий предъяв­ляется испытуемому, мы уменьшаем неопределенность. Как уже говорилось, деление этого уменьшения на уменьшаемую дисперсию (S² _комб) превращает ответ в отношение. Тем самым ω² сообщает нам часть, на ко­торую уменьшается неопределенность при знании экс­периментального 189условия. Это и есть мера воздействия на поведение независимой переменной.

Задача: Вычислите est ω² для эксперимента, сравни­вающего условие В и Г, с 18 испытуемыми в каждой группе:

∑x²в=4700; ∑x²г=4900; ∑x²комб=15,000.

Ответ: est ω²=0,34.

Роберт Готтсданкер

ОСНОВЫ

ПСИХОЛОГИЧЕСКОГО

ЭКСПЕРИМЕНТА

190Глава 5

ВЫДЕЛЕНИЕ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ

В чем сходны следующие ситуации?

1. Женщина стоит внутри огромного деревянного ящика, в который могло бы поместиться пианино, и смотрит через “глазок” на десятилетнюю девочку-ин­дианку. Если девочка садится на стул у одного угла ящика и многократно нажимает на рычаг, то после каждого десятого нажатия женщина вкладывает шарик в металлическую трубку, через которую тот со стуком скатывается в пластмассовый лоток перед девочкой. Если же девочка садится на стул в другом конце ящи­ка, где никакого рычага нет, женщина все равно перио­дически посылает ей шарики.

2. Эластичная повязка на голове спокойно сидящего молодого человека прочно удерживает введенные в его ноздри две пластиковые трубки. Несмотря на то что вовсе не холодно, уши человека плотно прикрыты за­глушками. Делая вдох, он нажимает кнопку, приводя в действие два насоса, которые поочередно вдувают пор­ции воздуха с запахом гвоздики ему в ноздри.

3. Мать и ребенок находятся в комнате с еще одной молодой женщиной. Мать кладет ребенка в постельку и со словами “бай-бай, Томми” выходит из комнаты. Ребенок начинает кричать. Ровно через 60 секунд после ухода мать возвращается в комнату.

Вы, конечно, решили, что все это сцены из авангар­дистского театра абсурда. Ничего подобного! Это опи­сание трех психологических экспериментов из ряда других, которые будут обсуждены в этой главе. На их примере мы разберем проблему выделения независимой переменной. Эти эксперименты совершенно отличны от тех, о которых мы говорили ранее.

Во-первых, ни один из них, по всей вероятности, не дает результатов, которые могли бы немедленно быть использованы на практике, как, например, новый метод обучения испанскому языку или лучший способ инфор­мировать 191покупателя о ценах на продукты в универ­саме. Во-вторых, здесь независимая переменная более проста, чем описанные выше. Те, как правило, пред­ставляли собой сложные по составу “группы факто­ров”. Эту же можно определить как единичную пере­менную. Так, единственное, чем отличаются условия в эксперименте с обонянием, — это время поступления воздуха в каждую ноздрю. Напротив, когда сравни­ваются два метода обучения испанскому языку, то они оказываются различными не только по виду речи (раз­говорная или письменная), но и по используемым упражнениям, по числу проверок, по порядку ознаком­ления с темами и т. д. В-третьих, в обсуждаемых здесь экспериментах независимая переменная не только бо­лее изолирована, но и условия ее предъявления более тщательно “очищены”. Так, в эксперименте с обонянием для ослабления посторонних раздражителей на испы­туемого надевали наушники.

Напротив, в экспериментах, которые “улучшают” реальный мир (см. гл. 3), экспериментатор иногда спе­циально вводит осложняющие обстоятельства, чтобы приблизить обстановку эксперимента к реальности и тем самым повысить внешнюю валидность. Так, в экспери­менте с ночными посадками самолета было смодели­ровано движение второго самолета, о котором нужно было сообщать “на землю”.

Новые эксперименты помогут нам углубить понима­ние переменных, влияющих на поведение. Такие экспе­рименты уже можно назвать научными. Их результаты могут не сразу найти практическое применение. Такова первая особенность трех экспериментов, упомянутых в начале данной главы. Они не обязательно связаны с “практикой”. Но и слово “научный” следует употреб­лять с некоторыми оговорками. Весь смысл проведения экспериментов в том, чтобы через четкое и полное опи­сание связей между независимой и зависимой перемен­ными понять, что определяет поведение.

Вторая характерная черта — выделение единичной независимой переменной указывает на то, что если полученные данные будут использованы для лучшего понимания повеления, необходима более точная экспериментальная 192гипотеза. Когда Дион предположила, что поиск лучше вести без бинокля, она привела ряд дово­дов, как-то: ограниченность обзора в бинокле, отсутст­вие восприятия глубины. Если бы гипотеза подтверди­лась, то это могло бы быть следствием либо всех на­званных причин, либо некоторых из них, либо каких-то причин, не упомянутых вовсе. Чтобы выделить действи­тельную причину, требуются дальнейшие эксперименты. С этой целью мы должны изолировать независимую переменную и в нашей гипотезе, и в нашем экспери­менте.

Третья особенность перечисленных экспериментов— использование “чистых” условий. Это один из способов контролировать “шум” в эксперименте. Даже идеаль­ный эксперимент в том виде, как он был описан ранее, не всегда имеет “чистые” условия. Другими словами, даже предъявление одному и тому же испытуемому сра­зу двух условий независимой переменной не обеспечи­вает строгой проверки ее действия. Оба условия могут быть одинаково “нечистыми”, одинаково “зашумленными”. Например, двумя условиями могут быть два раз­ных количества лекарства — с одними и темп же при­месями. В этом случае действие чистого лекарства вы­явить невозможно.

Очевидно, что чем точнее рабочая гипотеза, тем вы­ше класс эксперимента. Как и ранее, эталоном при этом является безупречный эксперимент. Любой реальный эксперимент должен стремиться к безупречному. Безу­пречный в отношении внутренней валидности экспери­мент — это такой вариант идеального эксперимента, который мы можем назвать чистым экспериментом. Прежде всего это идеальный эксперимент со всеми вы­текающими отсюда последствиями, но этого мало. Чи­стый эксперимент (также практически недостижимый) требует еще, чтобы экспериментатор оперировал только с выделенной независимой переменной и ни с чем боль­ше. Более того, все другие переменные, которые могли бы воздействовать на поведение, остаются строго по­стоянными.

Одной из мер достижения этого является "очищение" условий независимой переменной, которое, как вы увидите, 193может привести даже к надеванию теплых наушников в августе. Другие способы обеспечения до­статочно высокой внутренней валидности мы уже об­суждали: это устранение систематического смешения с побочными переменными. Здесь, в лабораторных экспериментах, отличающих­ся от “естественных” (см. предыдущие главы), мы рас­смотрим некоторые новые виды смешения.

Смешения, описанные ранее, в основном проистека­ли из того факта, что одному и тому же испытуемому не могут быть предъявлены два разных условия одно­временно. Конечно, такое “процедурное” по своей при­роде смешение остается проблемой и в этих экспери­ментах, как и в любых других. Но в лабораторных экс­периментах, предполагающих выделение независимой переменной, существует также другая разновидность смешения. Она связана с тем, что экспериментатор не может создать совершенно, “чистые” условия независи­мой переменной, как того требует эксперимент. Гаррет Хардин, сведущий биолог, хорошо выразил сущность этой трудности, сказав: “Мы никогда не можем иметь дело с чем-то одним” (1972, с. 68). Поскольку это “од­но”, что интересует экспериментатора, неизбежно соеди­нено с чем-то “другим”, мы говорим о сопутствующем смешении.

Первая разновидность такого смешения вызвана артефактами эксперимента. Экспериментатор дорого бы дал, чтобы удалить только ту небольшую часть мозга животного, которая фигурирует в его эксперименталь­ной гипотезе. Но он не может этого сделать. Он непре­менно повредит другую ткань. Если теперь он сравнит свою экспериментальную группу (с частично удаленным мозгом) с контрольной группой (не подвергавшейся операции), то он смешает экспериментальную перемен­ную с искусственно вызванной переменной. Будет неяс­но, обусловлена ли разница в поведении двух групп животных удалением именно данной части мозга или оперативным вмешательством вообще?

Вторая разновидность сопутствующего смешения по­рождается не методикой эксперимента как таковой, а тем фактом, что независимая переменная “естественным” 194образом связана с другой переменной. Когда мать выходит из комнаты, оставив ребенка, его плач может быть вызван как тем, что ушла мать, так и тем, что он вообще остался один.

Избавление от подобного “естественного смеше­ния” — одна из главных забот экспериментатора, пы­тающегося выделить независимую переменную.

В связи с обсуждаемыми новыми экспериментами встает по-новому вопрос относительно внешней валид­ности, а именно — вопрос, тот ли эксперимент был про­веден. Эксперименты, направленные на выделение не­зависимой переменной, часто предпринимаются, чтобы проверить истинность теории. В настоящее время тео­рии, как правило, абстрактны, в то время как экспери­менты должны быть конкретными. Необходимо, чтобы конкретная методика эксперимента вполне соответство­вала экспериментальной гипотезе, изложенной в более абстрактных терминах.

Например, можно выдвинуть гипотезу, что отклоне­ния в поведении подростков преодолеваются более эф­фективно рациональным путем (“убеждением”), чем на­казанием. Экспериментатор должен применить какой-то конкретный вид наказания. Предположим, в качестве такового он выбрал неприятный звук зуммера (Ля Вуайе, 1973). Является ли этот звук адекватной экспери­ментальной операционализацией абстрактного термина наказание? Безусловно, нет. Скорее всего он будет дей­ствовать на рефлекторном уровне. (При этом может оказаться, что и самому экспериментатору придется на­деть наушники.) Итак, эксперименты можно оценивать и с точки зрения операциональной валидности.

Эта глава научит вас прежде всего более аналитично подходить к экспериментам, направленным на вы­деление независимой переменной. Предположим, вы чи­таете экспериментальную статью, в которой показы­вается, что независимая переменная оказалась неэф­фективной. Вам необходимо внимательно ее изучить, чтобы убедиться, что экспериментальные условия были достаточно “чистыми”. А теперь предположим, вы чи­таете статью, в которой, наоборот, показано, что неза­висимая переменная решающим образом влияла на за­висимую 195переменную. Прежде всего вы должны спро­сить себя, а не было ли это результатом сопутствующего смешения с другой переменной. Если вы полагаете, что такая возможность не исключена, вы должны суметь показать это на диаграмме (см. ниже). Еще лучше, если вы сможете придумать контрольный эксперимент. Следующее, на что вы должны обратить внимание, — это корректность экспериментальных действий — на­сколько они представляют переменные, заключенные в экспериментальной гипотезе. Вы еще глубже освоите проблему изоляции независимых переменных, если сами проведете несколько экспериментов (после изучения соответствующей литературы) и разберете их столь же строго, как разбирали эксперименты других.

Ознакомившись с материалом этой главы, вы долж­ны будете ответить на вопросы по следующим темам:

1. Тип экспериментальной гипотезы, проверяемой в экспериментах, которые направлены на более глубокое понимание поведения.

2. Очищение экспериментальных условий.

3. Сопутствующее смешение и что с ним делать.

4. Операциональная валидность.

5. Выбор испытуемых и обращение с ними в экспе­рименте.

6. Логика тем, представленных в последующих гла­вах книги.

Дата добавления: 2015-09-03