
|
Читайте также: |
Для каждой прямой задачи линейного программирования (ЛП) существует соответствующая ей двойственная задача ПЛ в другом пространстве переменных, но с тем же оптимальным значением целевой функции (если решение вообще существует). Обе задачи симметричны по отношению друг к другу, если их представить в матричной форме.
Прямая задача: Требуется найти максимальное значение целевой функции:
 , (1)
, (1)
в условиях следующих ограничений:
 , (2)
, (2)
 . (3)
. (3)
где:
 – скалярная целевая функция прямой задачи ЛП;
– скалярная целевая функция прямой задачи ЛП;
 – вектор коэффициентов целевой функции;
– вектор коэффициентов целевой функции;
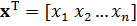 – вектор переменных прямой задачи;
– вектор переменных прямой задачи;
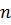 − число переменных прямой задачи;
− число переменных прямой задачи;
 – вектор ограничений прямой задачи;
– вектор ограничений прямой задачи;
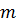 − число ограничений;
− число ограничений;
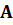 =
=  – (
– ( ) матрица коэффициентов ограничений.
) матрица коэффициентов ограничений.
Двойственная задача: Требуется найти максимальное значение целевой функции:
 , (1’)
, (1’)
в условиях следующих ограничений:
 , (2’)
, (2’)
 . (3’)
. (3’)
где:
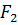 – скалярная целевая функция двойственной задачи ЛП;
– скалярная целевая функция двойственной задачи ЛП;
 – вектор коэффициентов целевой функции;
– вектор коэффициентов целевой функции;
 – вектор переменных двойственной задачи;
– вектор переменных двойственной задачи;
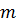 − число переменных двойственной задачи;
− число переменных двойственной задачи;
 – вектор ограничений двойственной задачи;
– вектор ограничений двойственной задачи;
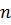 − число ограничений;
− число ограничений;
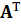 =
=  – (
– ( ) матрица коэффициентов ограничений.
) матрица коэффициентов ограничений.
Симметричность этих задач состоит в том, что постановка двойственной задачи к двойственной совпадает с исходной прямой задачей. Вектор ограничений  (вектор-столбец правых частей ограничивающих условий) прямой задачи становится вектором коэффициентов
(вектор-столбец правых частей ограничивающих условий) прямой задачи становится вектором коэффициентов  целевой функции двойственной задачи, и наоборот. Строки матрицы ограничений
целевой функции двойственной задачи, и наоборот. Строки матрицы ограничений 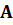 прямой задачи становятся столбцами матрицы ограничений
прямой задачи становятся столбцами матрицы ограничений 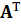 двойственной задачи. Каждая двойственная переменная связана с соответствующими ограничениями прямой задачи.
двойственной задачи. Каждая двойственная переменная связана с соответствующими ограничениями прямой задачи.
Теорема (двойственность задач ЛП). Если одна из задач двойственной пары имеет конечное оптимальное решение, то и другая также имеет конечное оптимальное решение, причем экстремальные значения целевых функций равны.
В справедливости теоремы можно убедиться непосредственным вычислением целевых функций. Найдем оптимальное значение вектора переменных  прямой задачи ЛП из неравенства (2):
прямой задачи ЛП из неравенства (2):
 , (4)
, (4)
где 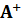 − псевдообратная матрица.
− псевдообратная матрица.
Число строк m и число столбцов n при транспонировании меняются местами: в двойственной задаче матрица 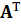 содержит n строк и m столбцов. Это необходимо учитывать при определении формул для вычисления псевдообратной матрицы.
содержит n строк и m столбцов. Это необходимо учитывать при определении формул для вычисления псевдообратной матрицы.
После подстановки правой части (4) в (1) найдем максимальное значение целевой функции прямой задачи ЛП:
 . (5)
. (5)
Найдем оптимальное значение вектора переменных  двойственной задачи ЛП из неравенства (2’):
двойственной задачи ЛП из неравенства (2’):
 , (4’)
, (4’)
После подстановки правой части (4’) в (1’) найдем минимальное значение целевой функции двойственной задачи ЛП:
 . (5’)
. (5’)
Правые части неравенств (5) и (5’) равны  , следовательно:
, следовательно:
 =
=  . (6)
. (6)
Что и требовалось доказать.
do not put all your eggs in a basket – не клади все яйца в одну корзину.
Дата добавления: 2015-09-03; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод псевдообратной матрицы | | | Введение |