
Читайте также:
|
Для прямоугольных платежных матриц обратная матрица, в обычном смысле, не существует, поэтому для вычисления вероятностей стратегий и цены игры применяют обобщенные обратные матрицы – псевдообратные матрицы. Для прямоугольных матриц полного ранга  размера (
размера ( ), где m – число строк, n – число столбцов, формулы вычисления псевдообратной матрицы
), где m – число строк, n – число столбцов, формулы вычисления псевдообратной матрицы 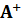 имеют следующий вид:
имеют следующий вид:
 .
.
Число строк m и число столбцов n при транспонировании меняются местами: в транспонированной матрице n – число строк, m – число столбцов. Это необходимо учитывать при определении формул для вычисления псевдообратной матрицы.
Применение псевдообратной матрицы, для вычисления векторов 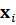 и
и 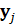 , дает также единственное решение игровой задачи
, дает также единственное решение игровой задачи  . Это решение, однако, является более точным решением, чем найденное методом обратной матрицы в задаче с удалёнными дублирующими и доминирующими строкам и столбцами, поскольку применяется для полной исходной платежной матрицы.
. Это решение, однако, является более точным решением, чем найденное методом обратной матрицы в задаче с удалёнными дублирующими и доминирующими строкам и столбцами, поскольку применяется для полной исходной платежной матрицы.
Методику применения методов обращения платежных матриц рассмотрим на примере.
Пример. [Кремер, стр. 191] Поставщик может поставлять три вида продукции: А 1, А 2 и А 3, получая при этом прибыль, зависящую от состояния спроса В 1, В 2, В 3 и В 4. В таблице 1 даны коэффициенты 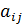 , характеризующие прибыль в условных единицах, которую получит поставщик, поставляя продукцию
, характеризующие прибыль в условных единицах, которую получит поставщик, поставляя продукцию 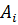 , если состояние спроса
, если состояние спроса  .
.
Таблица 1.
| B 1 | B 2 | B 3 | B 4 | |
| A 1 | 3,0 | 3,0 | 6,0 | 8,0 |
| A 2 | 9,0 | 10,0 | 4,0 | 2,0 |
| A 3 | 7,0 | 7,0 | 5,0 | 4,0 |
Требуется определить оптимальную стратегию поставок продукции, гарантирующую среднюю прибыль при любом спросе.
Решение. Рассмотрим процедуры вычисления оптимальных стратегий (пропорций) А 1, А 2, А 3 и В 1, В 2, В 3, В 4 двумя методами: методом обратной матрицы и методом псевдообратной матрицы, и сравним найденные решения.
1. Решим задачу методом обратной матрицы. Игровая модель задачи задается платежной матрицей 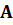 размера
размера 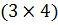 :
:
| B 1 | B 2 | B 3 | B 4 | ||
| 3,0 | 3,0 | 6,0 | 8,0 | А 1 | |
| A= | 9,0 | 10,0 | 4,0 | 2,0 | А 2 |
| 7,0 | 7,0 | 5,0 | 4,0 | А 3 |
Очевидно, что дублирующих стратегий у игроков нет. Стратегия В 2 доминирует стратегию B 1. Это означает, что для игрока В стратегия В 2 невыгодна (средний проигрыш больше), поэтому столбец В 2 можно удалить. У игрока А доминирующих строк нет. В результате удаления столбца В 2, получаем квадратную платежную матрицу A размера  :
:
| B 1 | B 3 | B 4 | ||
| 3,0 | 6,0 | 8,0 | А 1 | |
| A= | 9,0 | 4,0 | 2,0 | А 2 |
| 7,0 | 5,0 | 4,0 | А 3 |
Обратная матрица  равна:
равна:
| 0,273 | 0,727 | -0,909 | |

| -1,000 | -2,000 | 3,000 |
| 0,773 | 1,227 | -1,909 |
Найдем вспомогательный вектор  :
:

| 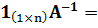
| 0,045 | -0,045 | 0,182 |
где 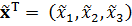 .
.
По определению  , поэтому принимаем
, поэтому принимаем  :
:

| 0,045 | 0,0 | 0,182 |
и вычисляем сумму 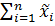 :
:
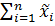 = =
| 0,227. |
Находим оптимальные вероятности (частоты) применения своих стратегий стороной А:
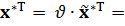
| 0,20 | 0,00 | 0,80 |
где учтено, что цена игры равна:
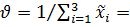
| 4,40. |
Таким образом, гарантированный средний выигрыш игрока А, найденный методом обратной матрицы, составляет 4,40 условных единицы, при поставке 20% продукции А 1 и 80% продукции А 3, при любом спросе В j.
2. Найдем решение методом псевдообратной матрицы. Полный ранг прямоугольной платежной матрицы 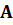
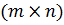 должен быть равен меньшему значению из чисел m и n. В рассматриваемой задаче число строк m = 3, число столбцов n = 4,
должен быть равен меньшему значению из чисел m и n. В рассматриваемой задаче число строк m = 3, число столбцов n = 4,  = m + n – 1= 3 + 4 – 1= 6.
= m + n – 1= 3 + 4 – 1= 6.
Поскольку 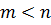 , псевдообратная матрица вычисляется по формуле:
, псевдообратная матрица вычисляется по формуле:
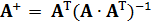 ,
,
где: матрица 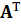 – транспонированная матрица
– транспонированная матрица 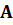 :
:
| A1 | A2 | A3 | |
| 3,0 | 9,0 | 7,0 | |
| AT = | 3,0 | 10,0 | 7,0 |
| 6,0 | 4,0 | 5,0 | |
| 8,0 | 2,0 | 4,0 |
произведение платежной матрицы 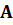 и транспонированной
и транспонированной 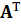 :
:
| 118,0 | 97,0 | 104,0 | |
A 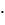 AT = AT =
| 97,0 | 201,0 | 161,0 |
| 104,0 | 161,0 | 139,0 |
обратная матрица 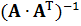 :
:
| 0,439 | 0,710 | -1,151 | |
(A 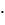 AT) -1 = AT) -1 =
| 0,710 | 1,216 | -1,940 |
| -1,151 | -1,940 | 3,115 |
псевдообратная матрица 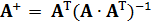 :
:
| -0,350 | -0,504 | 0,895 | |
| A+ = | 0,360 | 0,713 | -1,045 |
| -0,279 | -0,575 | 0,911 | |
| 0,331 | 0,353 | -0,627 |
Найдем вспомогательный вектор  :
:

| 0,062 | -0,013 | 0,134 |
По определению  , поэтому принимаем
, поэтому принимаем  :
:

| 0,062 | 0,00 | 0,134 |
и вычисляем сумму 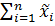 :
:
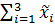 = =
| 0,196. |
Находим оптимальные вероятности (частоты) применения своих стратегий стороной А:
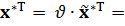
| 0,315 | 0,00 | 0,685 |
где учтено, что цена игры равна:

| 5,098. |
Таким образом, гарантированный средний выигрыш игрока А, найденный методом псевдообратной матрицы, составляет 5,098 условных единицы, при поставке 31,5% продукции А 1 и 68,5% продукции А 3, при любом спросе В j.
Очевидно, что точное решение игровой задачи методом псевдообратной матрицы дает большее значение гарантированного среднего выигрыша 5,098 > 4,40 на 13,7%, за счет большей на 6,5% поставки продукции А 1 и меньшей на 6,5% поставки продукции А 3.
Дата добавления: 2015-09-03; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод обратной платёжной матрицы | | | Двойственность задач линейного программирования |