Метод обратной платёжной матрицы

Этот метод позволяет находить решение игровых задач только с квадратными платежными матрицами размерности , содержащих только активные стратегии (по n стратегий c каждой стороны). Активными стратегиями игрока называются те смешанные стратегии с наибольшими весами или вероятностями, которые он неизменно и последовательно будет применять в игре.

Метод обратной матрицы применим в следующих условиях:

1. Из платёжной матрицы удалены дублирующие и доминирующие (заведомо невыгодные) стратегии.

2. Установлено отсутствие седловой точки.

Из теоремы Фробениуса-Перрона следует, что положительные матрицы А (с элементами , не имеющие дублирующих или линейно зависимых строк и столбцов являются невырожденными (определитель матрицы ).

Математическая модель игры, в этом случае, задаётся квадратной платежной матрицей размерности :

,

которая имеет обратную матрицу:

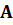где – адьюнкта матрицы , вычисляется по формуле:

,

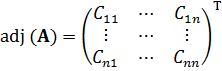здесь:

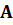
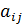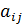– алгебраическое дополнение элемента матрицы , – минор элемента матрицы , .

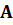В игровой задаче без седловой точки требуется определить оптимальные смешанные стратегии игроков , обеспечивающие гарантированную цену игры .

Для определения оптимальной смешанной стратегии игрока , составим систему уравнений в предположении, что применяет свою оптимальную смешанную стратегию, а – свои частные стратегии:

,

и учтем условие нормировки . Для компактности, запишем эту систему уравнений в векторно-матричной форме:

, (1)

где – вектор-строка размерности , состоящий из одних единиц.

Умножим обе части равенства справа на :

.

Произведение матрицы 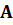и обратной матрицы равно единичной диагональной матрице :

.

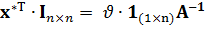В явном виде единичную матрицу не пишут, поэтому система уравнений (1) в нормальной форме записи относительно искомых вероятностей имеет следующий вид:

.

Рассмотрим новый вектор вспомогательных переменных :

Поскольку , справедлива цепочка равенств:

из которой следуют:

а) формула для расчета цены игры для игрока А:

б) формула для расчета вероятностей применения стратегий стороной :

Вывод формул вычисления цены игры и вероятностей стратегий стороны В аналогичен. Запишем систему уравнений для вероятностей стратегий в векторно-матричной форме:

,

или:

. (2)

Для игрока В вводятся вспомогательные переменные .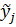

Формула вычисления цены игры через вспомогательные переменные 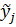для игрока В имеет вид:

Вероятности 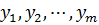применения стратегий стороной вычисляются по формуле:

Как видим, формулы для вычисления вероятностей стратегий и цены игры игрока В имеют ту же структуру, что и для стороны А, только определяются они через вспомогательные переменные .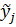

Отметим, что в силу существования и единственности обратной матрицы , решение игровой задачи при отсутствии седловой точки существует и единственное.

Дата добавления: 2015-09-03