
|
Читайте также: |
Несмотря на значительные успехи математической теории исследования операций, методы этой теории, гарантирующие оптимальный результат, очень мало применяются на практике. Причин здесь много, но мы отметим одну.
Практически вся математическая теория исследования операций развивалась математиками, стремящимися, прежде всего, исследовать наиболее общие свойства изучаемых задач. При этом неизбежно упрощались особенности, весьма существенные в конкретных приложениях. Поэтому, имея на вооружении математические методы исследования операций, в каждой прикладной задаче приходится искать конкретное решение, привлекая опыт и математиков и практических работников.
На выбор математических методов теории игр в исследовании операций, рассмотренных в учебном пособии, повлияли три фактора. Во-первых, решение практических задач осуществляется в условиях неопределённости поведения всех участников совместной деятельности. Во-вторых, по условиям задач логистики, требуется построить стратегию действий так, чтобы гарантировать оптимальный результат при любых возможных возмущениях. В-третьих, все участники совместной деятельности стремятся реализовать собственные стратегии достижения своих целей, которые часто противоположны целям других участников.
Напомним, кратко, основные положения и термины теории игр. Игрой называют конфликтные ситуации при совместной деятельности двух участников А и В, имеющих конечное число стратегий достижения противоположных целей.
Пусть игрок А имеет m стратегий: А 1, А 2, …, Аm, а игрок В – n стратегий: В 1, В 2, …, Вn. Каждой паре стратегий (Аi, Вj), когда А применяет свою стратегию Аi, а В – стратегию Вj, ставится в соответствие символ 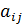 , числовое значение которого равно выигрышу игрока А у игрока В (если
, числовое значение которого равно выигрышу игрока А у игрока В (если 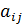 > 0), или проигрышу игрока А игроку В (если
> 0), или проигрышу игрока А игроку В (если 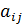 < 0).
< 0).
Коэффициенты 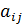 можно записать в виде таблицы, размером
можно записать в виде таблицы, размером 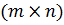 , где m – число строк, n – число столбцов таблицы. В этой таблице каждой стратегии Аi соответствует i -я строка, а каждой стратегии Вj – j -й столбец,:
, где m – число строк, n – число столбцов таблицы. В этой таблице каждой стратегии Аi соответствует i -я строка, а каждой стратегии Вj – j -й столбец,:
| B1 | B2 | … | Bn | ||
| A1 | a11 | a12 | … | a1n | |
| A = | A2 | a12 | a22 | … | a2n |
| … | … | … | … | … | |
| Am | am1 | am2 | … | аmn |
Игровая задача состоит в том, чтобы найти такие стратегии игры сторон А и В, которые приводят к наилучшему результату в том смысле, который определен правилами игры.
В случае одного показателя результативности игры, конфликтная ситуация может быть полностью описана матрицей размерности 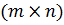 , которая, в теории игр, называется платежной матрицей:
, которая, в теории игр, называется платежной матрицей:
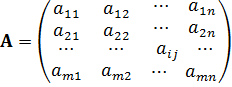 .
.
Прежде чем приступать к решению игровой задачи, необходимо определить особенности платежной матрицы:
- дублирующие стратегии,
- невыгодные стратегии,
- седловые точки.
В матрице игры i -я стратегия дублирует j -ю стратегию, если:
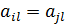 для
для 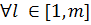 или
или  для
для 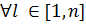 .
.
Невыгодные (проигрышные) стратегии определяются с помощью отношений доминирования. Если каждой стратегии игрока А поставить в соответствие вектор-строку матрицы А, то стратегия Аi, будет доминировать стратегию Аj, при выполнении следующего условия:
 для
для 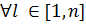 ,
,
В этом случае стратегия Аj будет заведомо невыгодной, и соответствующая строка из платежной матрицы А удаляется.
Если каждой стратегии игрока В поставить в соответствие вектор-столбец платежной матрицы А, то стратегия Вj будет доминировать над стратегией Вi при выполнении следующего условия:
 для
для 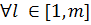 .
.
В этом случае стратегия Вj будет заведомо невыгодной, и соответствующий столбец из платежной матрицы А удаляется.
Поиск седловых точек выполняется по следующей схеме. В каждой строке матрицы А находят минимальный элемент:

и среди них определяется максимальный: 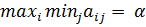 .
.
В каждом столбце матрицы А находят максимальный элемент:
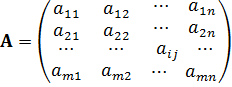
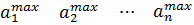
и среди них определяется минимальный:  .
.
Если  , то
, то 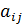 – седловая точка. Соответствующая седловой точке пара стратегий (Аi, Вj) называется оптимальной чистой стратегией, которая определяет точку равновесия конфликтной ситуации (игры). Значение
– седловая точка. Соответствующая седловой точке пара стратегий (Аi, Вj) называется оптимальной чистой стратегией, которая определяет точку равновесия конфликтной ситуации (игры). Значение 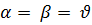 называется чистой ценой игры, или решением игровой задачи.
называется чистой ценой игры, или решением игровой задачи.
Цена игры всегда имеет нижнюю границу 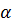 и верхнюю границу
и верхнюю границу 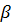 :
:
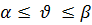 .
.
В случае, если равновесной ситуации нет, то оптимальное решение в чистых стратегиях отсутствует и приходится искать его в смешанной стратегии, предполагая, что число повторений игры достаточно для ранжирования стратегий по вероятностям их применения (по средним «весам», по «долям»,«пропорциям»). Задача состоит в определении такого набора стратегий игрока А, которые обеспечивают гарантированный выигрыш при наиболее вероятном действии противоположной стороны.
Обозначим вероятности применения игроком А своих стратегий Аi m -мерным вектор-столбцом x, где m – число стратегий игрока А:
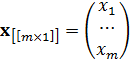 .
.
Элементы x i вектора x определяют вероятность применения игроком А своей i -й стратегии А i. Для описания вероятностей применения стратегий В j игрока В введём n -мерный вектор столбец y, где n – число стратегий В j:
 .
.
Элементы этих векторов должны удовлетворять условиям нормировки полной группы событий:


Чистая стратегия является частным случаем смешанной стратегии, когда пара оптимальных стратегий 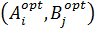 имеет вероятность совместного события равную единице, остальные – нулю.
имеет вероятность совместного события равную единице, остальные – нулю.
В смешанных стратегиях каждая ситуация в чистых стратегиях  является случайным событием. В силу независимости наборов вероятностей
является случайным событием. В силу независимости наборов вероятностей  ,
, 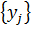 каждая ситуация в чистых стратегиях реализуется с вероятностью совместного события
каждая ситуация в чистых стратегиях реализуется с вероятностью совместного события 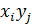 , которой соответствует выигрыш
, которой соответствует выигрыш 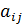 . Математическое ожидание выигрыша
. Математическое ожидание выигрыша 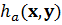 игрока А, в смешанных стратегиях, будет определяться следующим образом:
игрока А, в смешанных стратегиях, будет определяться следующим образом:
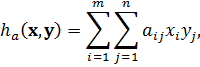
или в векторно-матричной форме:
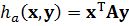 ,
,
где 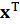 – транспонированный в строку вектор-столбец x.
– транспонированный в строку вектор-столбец x.
Оптимальными смешанными стратегиями  игроков А и В называются те стратегии, которые удовлетворяют следующим условиям:
игроков А и В называются те стратегии, которые удовлетворяют следующим условиям:
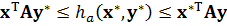 .
.
Выигрыш, соответствующий оптимальным смешанным стратегиям, называется ценой игры  :
:
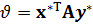 . (1)
. (1)
Основная теорема теории игр утверждает, что каждая конечная игра имеет, по меньшей мере, одно решение, возможно, в области смешанных стратегий.
Эта теорема имеет большое практическое значение: она даёт конструктивные методы поиска оптимальных стратегий при отсутствии седловой точки.
Дата добавления: 2015-09-03; просмотров: 109 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Жити по правді | | | Метод обратной платёжной матрицы |