Передача теплоты через плоскую однослойную и многослойную стенки и граничных условиях III рода

Рассмотрим однородную и изотропную стенку толщиной d с постоянным коэффициентом теплопроводности l. Заданы также температуры окружающей среды tж1 и tж2, а также коэффициенты теплоотдачи a1 и a1, причем все эти параметры также постоянны и не меняются вдоль поверхности. Следовательно, температура будет изменяться только в направлении, перпендикулярном плоской стенки.

Необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки.

Плотность теплового потока от горячей жидкости к стенке определяется по уравнению Ньютона-Рихмана:

q = a₁ (t_ж1 – t_с1).

При стационарном тепловом режиме та же плотность теплового потока, обусловленная теплопроводностью через твердую стенку будет равна:

.

Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи:

q = a₂ (t_с2 – t_ж2).

Представленные выражения можно записать в виде:

,

,

.

Складывая почленно полученные равенства, получим:

.

Отсюда плотность теплового потока равна:

.

Обозначим .

Тогда ,

где k – коэффициент теплопередачи, Вт/(м²×К).

Коэффициент теплопередачи k характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.

Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи, (м²×К)/Вт:

,

где и - внешние термические сопротивления,

- термическое сопротивление стенки.

Для многослойной стенки нужно учитывать термическое сопротивление каждого слоя. Если стенка состоит из n слоев, то полное термическое сопротивление теплопередачи через такую стенку будет равно:

,

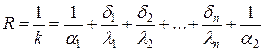
отсюда .

Плотность теплового потока через многослойную стенку, состоящую из n слоев, будет равна:

.

Тепловой поток Q через поверхность F твердой стенки равен:

.

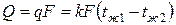Температуры поверхностей однородной стенки можно найти из уравнений:

; или .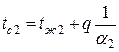

Температура на границе любых двух слоев i и i + 1 при граничных условиях третьего рода может быть определена по уравнению:

.

Лекция

Тема: «ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ»

(продолжение)

План.

4. Передача теплоты через цилиндрическую стенку и граничных условиях I рода.

5. Передача теплоты через многослойную цилиндрическую стенку и граничных условиях I рода.

6. Передача теплоты через однослойную и многослойную цилиндрические стенки и граничных условиях III рода

7. Критический диаметр цилиндрической стенки.

8. Передача теплоты через ребристую стенку.

9. Теплопроводность при наличии внутренних источников теплоты.

Передача теплоты из одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включается в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.

Дата добавления: 2015-09-03