Закон больших чисел и его след-вие. Нер-ство Чебышева.

Закон больших чисел в тер вер утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распр-ния близко к теоретич среднему (мате ожиданию) этого распределения. В зав-ти от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вер-сти, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое кол-во испытаний, при кот с любой заданной наперёд вероятностью частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общ смысл закона больших чисел — совместное действие большого числа случ факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вер-сти на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Закон больших чисел – это несколько теорем, опр-щих общ усл, при кот среднее значение случайных величин стремится к некоторой const при проведении большого числа опытов (теоремы Чебышева и Бернулли).

Если существует последовательность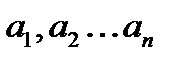

таких, что для любых ε>0, выполняется условие:

(*)

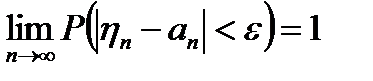Последовательность подчиняется закону больших чисел с заданными функциями :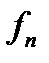

Если в выражении (*) , то говорят, что случайная величина 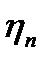сходится по вероятности к а.

В данных терминах 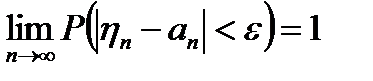означает, что вел-на η_n-a_n сходится по вероятности к нулю.

Неравенство Чебышева

Для любой случайной величины ξ(кси), имеющей M[ξ] и D[ξ] при каждом ε>0 имеет место неравенство(неравенство Чебышева):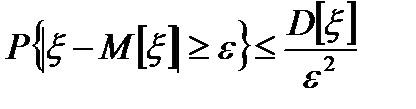

Док-во: ξ£η, M[ξ]£M[η]

Рассмотр. некотор.сл.вел-ну η

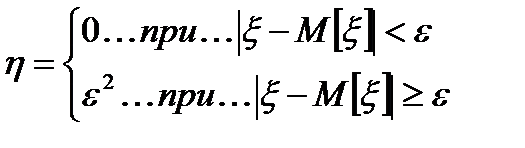
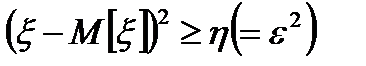
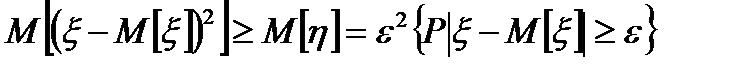
24. Закон больших чисел. Центральная предельная теорема.

Закон больших чисел утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распр-ния близко к теоретическому среднему (мат ожиданию) этого распределения.

limP(|1/n сумма (Xi)- a| <=e)=1
n-& i=1

Смысл закона закл. в том, что средние значения случайных величин стремятся к их мат. ожиданию при n- & по вероятн. отклонение средн. значений от мат.ожидания стан-ся сколь угодно малым с вероятностью, близкой к 1, если n достаточно велико или вероятность любого откл. средн. знач. от а сколь угодно мала с ростом n.

Центральная предельная теорема.Пусть 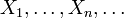есть бесконечная послед-сть независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние 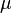и , соответственно. Пусть также .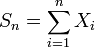

Тогда 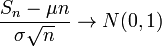по распределению при n ,

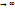где N (0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом 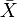выборочное среднее первых n величин, то есть , мы можем переписать результат центральной предельной теоремы в следующем виде: по распределению при n /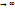

Дата добавления: 2015-10-23