Геометрическая вер-ть

Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вер-ть попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вер-ть того, что брошенная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле: 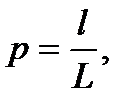где l – длина отрезка l, а L – длина отрезка L. Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вер-ти того, что она попадет на часть этой области s: . В трехмерном случае вер-ть того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:

5. Зависим и независимые события. Усл вер-ть. Теорема умножения вер-тей.

Усл вер-сть 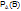соб.А наз-ся вер-ть соб.В при условии, что событие А произошло (пример: пусть соб.А - это извлечение из колоды в 32 карты туза; соб.В – вторая вынутая карта из колоды оказалось тузом. Если после 1-го раза карта возвращается в колоду, то вер-ть вынуть туз не меняется и равна 4/32, если же 1-я карта в колоду не возвращается, то осуществление соб.А прибудет к тому, что в колоде остается 31 карта из которой 3 туза 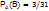– условная вер-ть)

Т-ма умножения зависимых событий: вер-ть произведения двух событий равна произведению вер-ти одного соб на условную вер-ть другого, при усл, что 1-ое событие произошло: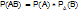

Док-во: Пусть n-число возможных исходов опыта; m_А-число исходов благоприятствующих соб.А; m_B-//-соб.В, m_АВ – число исходов опыта, при кот происходят оба события,. для вычисления усл вер-ти 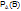, множеством возможных исходов нужно считать m_А(т.к. А произошло), а множеством благ-тных исходов, необходимо считать исходы, при кот произошли и А, и В.

=>

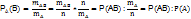
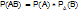
Пример: для поражения цели необходимо попасть в неё дважды. Вер-ть 1-го попадания 0,2, затем она не меняется при промахах, но после 1-го попадания увеличивается в 2 раза. Найти вер-ть того что цель будет поражена первыми двумя выстрелами.

Решение: соб.А – попадания при первом выстреле

Соб.В - //- при 2-ом выстреле

, ,

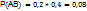
А и В совместные события

Пусть вер-ть соб.В не зависит от появления соб.А

Событие В называют независимым от соб А, если появление соб.А не изменяет вер-ти события В, т.е. если условная вер-ть соб.В равна его безусловной вер-ти:

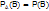подставив данное равенство в

получим

, отсюда

,т.е.условная вер-ть соб.А в предположении, что наступило соб.В, равна его безусловной вер-ти. Другими словами, соб.А не зависит от соб.В. След-но и соб.А не зависит от соб.В; это значит, что св-во незав-сти событий взаимно.Для независ соб т-ма умнож 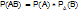имеет вид ,

Т.е. вер-ть совместного появления двух независимых событий равна произведению вер-тей этих событий.

Два события называют независимыми, если вер-ть их совмещения равна произведению вер-тей этих событий; в противном случае события называют зависимыми.

6.Формула полной вер-ти. Формула Бейеса.

Опр.: пусть событие А может произойти только совместно с одним из событий Н₁, Н₂,…,Н_nобразующих полную группу несовместных событий, тогда соб. Н₁, Н₂,…,Н_nназываются гипотезами.

Теорема: вер-ть соб.А наступающего совместно с гипотезами Н₁, Н₂,…,Н_nравна:

- формула полной вер-ти

где, Р(Н_i) – вер-ть i-той гипотезы,Р_Нi(А) – вер-ть соб.А при усл реализации гипотезы Н_i

Док-во: соб.А можно считать суммой попарно несовместных событий АН_1, АН₂, …АН_n несовместные события, тогда из теорем сложения вер-тей:

Р(А)+Р(АН₁+…+ АН_n)=Р(АН₁)+…+Р(АН_n)=

=Р_Нi(А)* Р(Н₁)+…+ Р_Нn(А)* Р(Н_n)=

Теорема гипотез (формула Байеса) – следствие т-мы умнож и ф-лы полной вер-ти. Имеется группа несовместных гипотез H1,H2...Hn, чьи вер-ти равны соотв-но P(H1),P(H2)...P(Hn). В рез. Σ происходит событие А. Как следует изменить вер-ти гипотез в связи с появлением А (найти усл вер-ть P(Hi|A))? Выражая P(A) из ф-лы полной вер-ти, имеем соотношение Байеса: 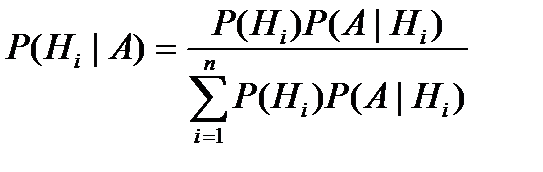.Док-во: вер-ть появления А опред. по ф-ле полной вер-ти 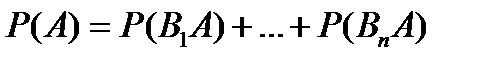Поищем условные вер-ти при усл, что произошло событие А. По теореме умножения имеем 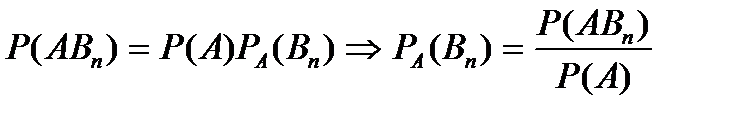. Подставим P(A), получим . чтд. Ф-лы Байеса позволяют переоценить вер-ти после того, как становится известным результат испытания, в итоге которого появилось событие А.

Дата добавления: 2015-10-23