Основные узлы

Эти два вида коробок передач являются комбинациями нескольких основных узлов в разных вариантах.

Рассмотрим подробно устройство таких узлов в следующем порядке:

1. Цилиндрическая зубчатая передача с неподвижными осями (вальная).

2. Планетарная зубчатая передача.

3. Гидромуфта.

4. Гидротрансформатор.

Определим основные соотношения в зубчатых передачах.

1. Зубчатая передача цилиндрическая с неподвижными осями внешнего зацепления (вальная)

Кинематическая схема такой передачи представлена на рис.13, где слева показана передача, состоящая из пары шестерен 1 и 2 с неподвижными осями О₁ и О₂ и имеющих соответственно Z₁ и Z₂ зубьев. Справа на рисунке показана проекция этой передачи с указанными на ней направлениями вращения шестерён. Ведущей будем считать шестерню 1, ведомой – шестерню 2. В зацеплении могут работать зубчатые колеса (шестерни) с одинаковым модулем, т.е. с одинаковой длиной основания зуба. Таким образом, число зубьев шестерни в другом масштабе – это длина окружности (делительной).

Зубчатая передача передает мощности с преобразованием вращающего момента и частоты вращения.

Главная характеристика зубчатой передачи – это передаточное число, представляющее собой отношение частоты вращения ведущего колеса w₁ к частоте вращения ведомого колеса w₂.

Обычно передаточное число обозначается буквой i с индексами. Для рассматриваемой передачи с неподвижными осями буква i снабжается индексами внизу: номер ведущего колеса – номер ведомого колеса. Для зубчатой пары рис.13 передаточное число обозначается так:

i₁₂=

Частота вращения колеса представляет собой производную от угла поворота по времени:

w₁= ; w₂= ;

где a и b - углы поворота колёс 1 и 2.

Таким образом, благодаря жесткой связи углов поворота зубчатых колес углу a поворота колеса 1 соответствует угол b поворота колеса 2, и передаточное число представляет собой отношение этих двух углов:

i₁₂= ;

Повернем ведущее колесо 1 на один оборот по часовой стрелке, тогда связанное с ним колесо 2 повернется против часовой стрелки на угол b = Z₁/Z₂; поворот ведущего колеса 1 на о дин оборот соответствует углу a = Z₁/Z₂ = 1, т.е. углы измеряются в относительных единицах – единица угла поворота – один оборот. При Z1< Z2, как это видно из рисунка, угол поворота колеса 2 больше единицы (ускоряющая передача).

Таким образом, передаточное число может быть выражено через числа зубьев:

і₁₂ = ;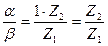

2. Зубчатая передача с подвижными осями (планетарная передача)

Простая планетарная передача имеет кинематическую схему, показанную на рис.14, где слева дана проекция передачи, имеющей эпициклическое колесо (коронное) 2, два или четыре сателлита 3, солнечное колесо 1, водило 4 (деталь, связывающая между собой оси сателлитов). На правой проекции для простоты показан один сателлит.

Особенностью планетарной передачи является то, что оси сателлитов подвижны и возможны разные варианты фиксации элементов передачи и различные величины передаточных чисел.

Определим передаточное число планетарной передачи при остановке (фиксации) коронного колеса (показано штриховкой на правой проекции, см. рис.14).

Рассчитаем передаточное число от ведущего солнечного колеса к ведомому водиле:

,

где верхний индекс к у передаточного числа обозначает зафиксированный элемент (коронное колесо).

a - угол поворота солнечного колеса,

b - угол поворота водила.

Прокатим сателлит 3 (число зубьев Z₃) по коронному колесу так, чтобы он сделал ровно один оборот и его первый зуб (обозначен кружочком) опять коснулся коронного колеса, как это показано на правой проекции рисунка. При этом водило (ось сателлита) повернется на угол b.

Следует обратить внимание на то, что это условный поворот сателлита ровно на один оборот. На самом деле, как это видно из рисунка, вертикальная ось сателлита при повороте водила на угол b повернулась на этот же угол при своем перемещении из начального положения в конечное. Вертикальная ось сателлита – это и есть водило.

Угол порота водила b = Z₃/Z₂, где Z₂ – число зубьев коронного колеса. Соответствующий угол поворота солнечного колеса с числом зубьев Z₁ определяется так: если бы ось сателлита была неподвижной, то поворот сателлита на один оборот (угол равен единице) вызвал бы поворот солнечного колеса на угол a′ = Z₃/Z₁, но так как сателлит катится по коронному колесу, то это вызывает дополнительный поворот солнечного колеса ещё на угол b. Таким образом полный угол поворота солнечного колеса (относительное и переносное движение) будет:

a = a¢ + b = ;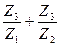

отсюда передаточное число

і = ;

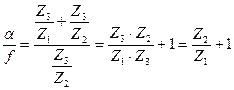Рассмотрим другой вариант фиксации: солнечное колесо неподвижно, ведущее – коронное колесо, ведомое – водило.

Повернём коронное колесо по часовой стрелке (рис.15) так, чтобы сателлит повернулся на один оборот (опять без учета переноса) вокруг солнечного колеса, тогда

b¢ = ,

где b¢ - угол поворота водила.

При этом коронное колесо повернулось бы на угол γ¢ = Z₃/Z₂ при неподвижной оси сателлита, а так как ось сателлита (водило) повернулось на угол b¢, то полный угол поворота коронного колеса

g = g¢+b¢= .

Передаточное число

,

индекс с – солнечное колесо.

Наконец осталось рассмотреть два последних случая. Водило неподвижно, ведущим является коронное колесо, ведомым – солнечное.

В этом случае передаточное число:

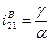
где g - угол поворота коронного колеса;

a - угол поворота солнечного колеса;

индекс В – водило.

Повернем коронное колесо по часовой стрелке так, чтобы сателлит сделал один оборот (рис.16), тогда

g = .

При этом солнечное колесо повернется на угол a = Z₃/Z₁, тогда

Последний вариант – водило неподвижно, ведущим является солнечное колесо, ведомым – коронное, тогда:

.

Последние два варианта, в которых водило неподвижно, превращают планетарную передачу в простую зубчатую передачу с неподвижными осями, при этом сателлит является паразитной шестернёй, не влияющей на передаточное число.

Сведем полученные результаты в таблицу 6.

Таблица 6

N п/п	Вид зубчатой передачи	Условия передачи	Передаточное число
1.	Цилиндрическая с неподвижными осями внешнего зацепления	Ведущее колесо – 1, ведомое 2, рис.13	І12 = Z2/Z1
2.	Простая планетарная передача	Коронное колесо неподвижно, ведущее колесо – солнечное, ведомое – водило, рис.14	І1В^К = Z2/Z1 + 1
3.	Простая планетарная передача	Солнечное колесо – неподвижно, ведущее коронное колесо, ведомое – водило, рис.15	І2В^С = Z1/Z2 + 1
4.	Простая планетарная передача	Водило неподвижно, ведущее – коронное колесо, ведомое – солнечное, рис.16	І21^В = Z1/Z2
5.	Простая планетарная передача	Водило неподвижно, ведущее – солнечное колесо, ведомое – коронное, рис.16	І12^В = Z2/Z1

3.Гидромуфты

Гидродинамическая муфта или кратко гидромуфта была изобретена Д.М.Михеевым в 1908 году.

Устройство гидромуфты и ее свойства рассмотрим на примере конструкции гидромуфты грузового автомобиля МАЗ-525, на котором последовательно соединялись гидромуфта и через короткую карданную передачу двухдисковое фрикционное сцепление. Поперечный разрез этой гидромуфты показан на рис.17, где 1 – ведущее лопастное насосное колесо (насос), 2 – ведомое лопастное турбинное колесо (турбина). Насос соединяется с коленчатым валом, турбина - с трансмиссией. Насос и турбина помещены в общем корпусе, заполненном на 80 % объема турбинным маслом. Каждое из колес выполнено в виде полутóра с плоскими радиальными лопатками. При вращении наоса под действием центробежным сил жидкость отбрасывается к периферии и перемещается из насоса в турбину по стрелке.

Передача энергии происходит только при наличии разности частот вращения насоса и турбины – турбина должна вращаться медленнее насоса. Тогда возникает момент вращения.

Гидромуфта осуществляет передачу энергии при постоянном моменте – момент насоса равен моменту турбины.

М_Н = М_Т

Ввиду того, что гидромуфта работает при разных частотах вращения насоса и турбины, то их мощности не одинаковы:

N = M_H × w_H;

N_T = M_T × w_T.

КПД гидромуфты:

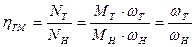
При неподвижной турбине h_ГМ=0, а момент М_Т максимален, характеристики 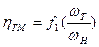и М_Т = 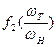показаны на графике рис.17.

4. Гидротрансформатор

Гидродинамический трансформатор или гидротрансформатор был изобретен в 1903 году немецким ученым Г.Феттингером и применялся вначале в энергетических установках судов.

Схема гидротрансформатора показана на рис.18, где Н – насосное колесо (насос), Т – турбинное колесо (турбина), Р – реактор или направляющий аппарат, соответственно моменты и частоты вращения w_Н, М_Н, w_Т, М_Т, М_Р.

На насосе, турбине, реакторе имеются лопасти специального профиля, насос – ведущий, турбина – ведомая, реактор неподвижен. При вращении насоса жидкость будет циркулировать по кругу, что показано на рис.18 стрелками.

Рассмотрим упрощённую расчётную схему, показанную на рис.19, где как и на рис.18, Н – насос, Т- турбина, Р - реактор, R – радиус насоса, турбины и реактора, V₁, V₂, V₃ – линейные средние скорости жидкости, М_Н, М_Т, М_Р – моменты насоса, турбины и реактора и их действие на жидкость показаны стрелками.

При установившемся движении системы, т.е. при постоянных частотах вращения:

М_Н = V₂ – V₁;

M_T = V₂ + V₃;

M_P = V₃ + V₁.

Эти выражения составлены в предположении, что все векторы скорости направлены по касательной к окружности радиуса R, а секундный и массовый расходы равны 1.

Уравнение моментов:

М_Н – М_Т + М_Р = V₂ – V₁ – V₂ – V₃ + V₃ + V₁ = 0,

Откуда

М_Н – М_Т + М_Р = 0,

Или

М_Н + М_Р = М_Т,

То есть момент турбины равен сумме моментов насоса и реактора, следовательно, момент турбины больше момента насоса:

М_Т > М_Н.

Таким образом, гидротрансформатор преобразует (увеличивает) момент.

Если исключить реактор, то есть положить его момент М_Р равным нулю, то получим уравнение гидромуфты и ее и её расчетную схему (рис.20).

При установившемся движении получим:

М_Н = V₂ – V₁;

М_Т = V₂ + V₃;

M_P = 0, то есть V₃ = -V₁.

Откуда

М_Н – М_Т = V₂ – V₁ – V₂ – V₃ = V₂ – V₁ – V₂ + V₁ = 0.

Следовательно, М_Н = М_Т.

Таким образом, если реактор будет вращаться как одно целое с насосом, то гидротрансформатор превращается в гидромуфту или переходит на режим гидромуфты.

Гидротрансформатор характеризуется основными параметрами: передаточным отношением i_ГТ, коэффициентом трансформации К, КПД h_ГТ, коэффициентом момента на валу насоса l_Н, коэффициентом прозрачности П.

Передаточное отношение

; ,

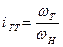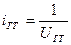где U_ГТ – передаточное число гидротрансформатора, w_Т, w_Н – угловые частоты турбины и насоса, как это было пояснено выше.

Коэффициент трансформации

К = .

Максимальное значение К соответствует остановленной турбине (i_ГТ = 0) и в зависимости от конструкции гидротрансформатора лежит в пределах 2…4.

КПД гидротрансформатора

,

h_ГТ = 0,85…,92 в рабочем диапазоне.

Гидротрансформатор в современных автомобилях используется как бесступенчатая часть комбинированной гидромеханической коробки передач. Это так называемый комплексный гидротрансформатор или гидротрансформатор системы Trilok – конструкция такова, что реактор установлен на муфте свободного хода. В комплексном гидротрансформаторе происходит автоматический переход с режима гидротрансформатора на режим гидромуфты, это делается для того, чтобы повысить КПД. В комплексном гидротрансформаторе КПД достигает значения 0,97. Кроме того, в современных гидротрансформаторах предусматривается его блокировка, то есть жёсткое соединение насоса с турбиной, в этом случае КПД достигает единицы.

Конструкция такого гидротрансформатор приведена на рис.21, где 1 – муфта блокировки, 2 – турбина, 3 – насос, 4 – реактор, 5 – муфта свободного хода (обгонная муфта).

Коэффициент момента насоса служит для определения нагрузки на лопастное колесо насоса:

l_Н = ,

где r - плотность рабочей жидкости,

D_ак – активный (наибольший) диаметр лопастного колеса (рис.18).

l_Н – безразмерный коэффициент, который определяет связь между моментов насоса и активным диаметром насоса. Аналогично определяется связь между моментов турбины и её диаметром.

М_Н º ,

Эта зависимость свидетельствует о том, что малое увеличение активного диаметра позволяет резко увеличит момент, то есть гидротрансформатор может при малых габаритах передавать большую мощность.

Коэффициент прозрачности П показывает, в какой степени гидротрансформатор способен нагружать двигатель:

П = ,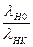

Где l _НО – коэффициент момента насоса при w_Т = 0;

l _НК – коэффициент момента насоса при К = 1.

Гидротрансформаторы могут быть в зависимости от конструкции двух видов:

1) непрозрачный гидротрансформатор (П = 1) – изменение режима работы турбины не изменяет режим работы насоса, а следовательно, и двигателя.

2) Прозрачный гидротрансформатор (П>1) – увеличение нагрузки турбины приводит к увеличению нагрузки насоса и двигателя (прямая прозрачность).

Дата добавления: 2015-10-31