Минимизация числа состояний абстрактного автомата

Два автомата называются эквивалентными, если они реализуют один и тот же алфавитный оператор. Задача минимизации числа состояний автомата формулируется следующим образом: задан автомат A и требуется построить эквивалентный автомат , имеющий минимальное число состояний.

Рассмотрим алгоритм минимизации числа состояний абстрактного автомата Мили A = < V,W,S,l,m,s (0)>. Задача решается за N шагов. Введем определения понятий, которые используются при описании алгоритма.

Определение: состояние s 1-эквивалентно состоянию , если и только если столбец таблицы выходов для состояния s совпадает со столбцом таблицы выходов для состояния .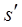

Определение: состояние s тождественно , т.е. s º , тогда и только тогда, когда и столбец таблицы переходов для s совпадает со столбцом таблицы переходов для .

Определение: состояние s k -эквивалентно состоянию для k ³2, если и только если состояние s (k -1)-эквивалентно состоянию и (k -1)-замещенный столбец таблицы переходов для s совпадает с (k -1)-замещенным столбцом таблицы переходов для .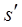

Определение: (k -1)- замещенным назовем столбец таблицы переходов, в котором каждый символ s Î S заменен на наименование (k -1)-класса, которому принадлежит s.

Алгоритм минимизации:

Шаг 1. Разбить множество состояний S на два или более 1-классов 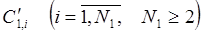по отношению 1-эквивалентности, которое обозначим .

Если разбиение на 1-классы невозможно, то автомат уже имеет минимальное число состояний и работа алгоритма заканчивается.

Если разбиение на 1-классы возможно, выявить в каждом 1-классе подклассы тождественных состояний по отношению тождественности º.

Оставить в каждом 1-классе по одному представителю каждого подкласса тождественных состояний: получим окончательные значения 1-классов .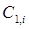

Шаг k. Разбить каждый (k -1)-класс на два или более k -подклассов по отношению k -эквивалентности.

Если ни один (k -1)-класс не поддается разбиению, то перейти к завершающему шагу N.

Шаг N. В полученном разбиении выбрать из каждого класса 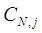по одному представителю состояний, которые и остаются в минимизированном автомате. Если в полученной таблице переходов имеются удаленные состояния, следует заменить их представителями соответствующих классов.

Пример 4. Автомата Мили задан таблицами выходов и переходов:

Шаг 1. Предварительное 1-разбиение есть , где и . Но s ₅º s ₇, потому отбрасываем из 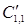состояние s ₇ и получаем окончательное 1-разбиение { C _1,1, C _1,2}, где C _1,1={ s ₁, s ₃, s ₅} и C _1,2={ s ₂, s ₄, s ₆, s ₈}. В столбце для s ₂ заменяем s ₇ на s ₅:

Шаг 2. 1-замещенная таблица переходов для класса C _1,1 есть

	s 1 s 3 s 5
v 1 v 2	C 1,1 C 1,2 C 1,2 C 1,2 C 1,1 C 1,1

Разбиваем C _1,1 на два 2-класса: C _2,1={ s ₁} и C _2,2={ s ₃, s ₅}. 1-замещенная таблица переходов для класса C _1,2:

	s 2 s 4 s 6 s 8
v 1 v 2	C 1,1 C 1,2 C 1,2 C 1,1 C 1,2 C 1,1 C 1,1 C 1,2

Разбиваем 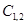на два 2-класса C _2,3={ s ₂, s ₈} и C _2,4={ s ₄, s ₆}.

Шаг 3. C _2,1 входит в окончательное разбиение, поскольку содержит только одно состояние. 2-замещенная таблица переходов для C _2,2:

	s 3 s 5
v 1 v 2	C 2,4 C 2,4 C 2,2 C 2,2

т.е. C _2,2 не поддается разбиению. 2-замещенная таблица для C _2,3:

	s 2 s 8
v 1 v 2	C 2,2 C 2,2 C 2,4 C 2,4

т.е. C _2,3 не поддается разбиению. 2-замещенная таблица для C _2,4:

	s 4 s 6
v 1 v 2	C 2,3 C 2,3 C 2,2 C 2,2

т.е. C _2,4 не поддается разбиению. Итак, поскольку дальнейшее разбиение невозможно, получено разбиение { C _2,1, C _2,2, C _2,3, C _2,4}. Выбираем в каждом классе по одному представителю, например: s ₁Î C _2,1, s ₂Î C _2,2, s ₃Î C _2,3, s ₄Î C _2,4. Тогда таблицы переходов и выходов минимизированного автомата:

Дата добавления: 2015-10-23