Способы описания конечных автоматов

Глава 1

АБСТРАКТНЫЕ АВТОМАТЫ

Понятие абстрактного автомата

Теория цифровых, или дискретных, автоматов это прикладной раздел дискретной математики, обеспечивающий теоретическую информатику. Теория автоматов изучает математические модели - автоматы. Автоматные модели используются для анализа функционирования и проектирования отдельных узлов вычислительных систем, для разработки программного обеспечения, а также могут быть использовании при создании моделей в других областях техники, биологии, медицине и т.д. […..].

Автомат можно представить как некоторое устройство (черный ящик), на которое поступают внешние воздействия (входные сигналы), имеющие внутреннее состояние автомата, причем реакция автомата (выходной сигнал автомата) на каждое воздействие зависит как от конкретного значения воздействия, так и от состояния автомата.

Множества дискретных воздействий, реакций и состояний представляются в теории абстрактных автоматов с помощью соответствующих алфавитов. Поэтому введем в рассмотрение алфавит (множество) входных сигналов V ={ v }, алфавит (множество) выходных символов W ={ w }, а также алфавит (множество) состояний автомата S ={ s }. Каждый входной символ v Î V отображает входное воздействие, а выходной символ w Î W реакцию автомата.

Предполагается, что множества V и W конечны. Если множество S конечно, то автомат называется конечным (finite automatum), а если S бесконечно, то автомат называется автоматом с бесконечным числом состояний. Если автомат имеет всего лишь одно состояние, то он называется тривиальным, или автоматом без памяти.

Цифровой автомат (ЦА) функционирует, т.е. изменяет свое состояние и вырабатывает выходную реакцию в результате очередного входного воздействия, в дискретные моменты времени. Поскольку конкретные значения времени в модели абстрактного автомата несущественны, будем использовать дискретное автоматное время t, принимающие последовательно целочисленные значения 0,1,2,..., прием t =0 соответствует начальному моменту, с которого рассматривается функционирование автомата.

Получая на входе последовательность (цепочку) входных символов v (0) v (1) v (2)… автомат вырабатывает последовательность (цепочку) выходных символов w (0) w (1) w (1)…. Функциональная зависимость выходной последовательности символов от входной последовательности автомата называется алфавитным оператором, реализуемым данным автоматом.

Алфавитный оператор автомата теоретически можно определить следующим образом

w (t)= l_v [ v (0) v (1) v (2)… v (t)], (1)

где l_v [×]- функция от цепочки t +1 входных символов. Функция l_v [×] дает значение выходного символа w (t) в момент времени t в зависимости от последовательности v (0) v (1) v (2)… v (t) символов, поступивших к этому моменту на входе автомата. Однако, практическое использование определения (1) в общем случае нереально, хотя бы потому, что автоматное время t может принимать сколь угодно большое значение, и, следовательно, потребовалось бы описать реакцию автомата для бесконечного множества входных последовательностей v (0) v (1) v (2)… v (t) при t ®¥.

На практике поступают следующим образом. Бесконечное множество входных последовательностей разбивается на классы (события) таким образом, что каждому классу соответствует некоторое состояние s Î S автомата, а именно, множество { v (0) v (1) v (2)… v (k)}_s входных последовательностей, приводящих автомат в некоторое состояние s Î S. Таким образом, состояние s можно рассматривать в качестве представителя множества { v (0) v (1) v (2)… v (k)} _s. Отметим, что в множество { v (0) v (1) v (2)… v (k)} _s для конкретного s могут входить цепочки v (0) v (1) v (2)… v (k) самой разной длины.

Итак, автомат может находиться в одном из множества S состояний. Если в момент времени t автомат находится в состоянии s (t) и на вход его поступает символ v (t) Î V, то в следующий момент времени t +1 автомат переходит в состояние s (t +1) в соответствии с функцией переходов

s (t +1)= l [ s (t), v (t)]. (2)

Функция переходов l [×,×] реализует отображение некоторого подмножества множества D_l Í S ´ V декартова произведения S ´ V в множество S. Если задано состояние автомата s (0)Î S в начальный момент t =0, то состояние его s (t +1) в момент t +1 является отображением входной последовательности v (0) v (1)… v (t). Функция переходов l [ s (t), v (t)] представляет это отображение как функцию двух аргументов: состояния s (t), представляющего цепочку v (0) v (1)… v (t- 1), и входного символа v (t).

Автомат Мили

Выходной символ автомата Мили в момент времени t определяется функцией выходов

w (t)= m [ s (t), v (t)]. (3)

Таким образом, функция выходов автомата Мили реализует отображение некоторого подмножества D_m Í S ´ V декартова произведения S ´ V в множество W. Иногда, для краткости используют обозначение: s⁺ = s (t +1), s = s (t), v = v (t), w = w (t). Тогда функция переходов автомата Мили запишется в виде s⁺ = l (s, v), а функция выходов в виде w = m (s, v).

Автомат называется полностью определенным, если D_l = D_m = S ´ V. В противном случае автомат называется частичным. Иными словами, у полностью определенного автомата области определения функций l [×,×] и m [×,×] совпадают с декартовым произведением S ´ V, а у частичного автомата эти функции определены на подмножествах D_l и D_m множества S ´ V.

Способность автомата фиксировать состояния, представляющие классы входных последовательностей (события), называют памятью автомата. Каждое состояние s Î S автомата представляет некоторый класс эквивалентности { v (0) v (1) v (2)… v (k)} _s входных последовательностей, поскольку поведение автомата в любой момент времени t зависит только от класса, т.е. s (t), и входного воздействия v (t). Такой подход позволяет устранить время как явную переменную и выразить выходные символы как функцию состояний и входных символов в данный момент времени, что находит выражение в общей записи модели A абстрактного автомата Мили:

A = < V,W,S,l,m,s (0)>, (4)

где

V,W,S - алфавиты входных, выходных символов и символов состояний соответственно;

l, m - функции переходов и выходов соответственно;

s (0) - начальное состояние.

Способы описания конечных автоматов

Для описания конечных цифровых автоматов можно использовать стандартные (автоматные) языки иначальные языки.

Стандартные, или автоматные, языки описывают функции переходов и выходов в явном виде, а именно в виде:

1) таблиц переходов и выходов;

2) графа, представляющего наглядно функции l и m.

Начальные языки описывают автомат на поведенческом уровне. К начальным языкам относятся:

1) языки логических схем и граф-схем алгоритмов;

2) язык регулярных выражений алгебры событий;

3) формальные и автоматные грамматики.

Если задано описание (4) полностью определенного автомата в стандартной форме, то для любого начального состояния автомата s (0) и последовательности входных символов v (0) v (1) v (2)… v (t) можно вычислить реакцию автомата в виде последовательности выходных символов w (0) w (1)… w (t).

Пример 1. Автомат ПРОДАВЕЦ газет получает монеты достоинством в 1 рубль и 2 рубля. Если сумма монет равна 3 рублям, то автомат выдает газету. Если сумма больше 3 рублей, то автомат возвращает все деньги. Введем обозначения входных и выходных символов и состояний автомата.

Входные символы:

v ₁ - опущена монета достоинством 1 рубль;

v ₂ - опущена монета достоинством 2 рубля.

Выходные символы:

w ₁ - сообщение "Принята сумма 1 руб.";

w ₂ - сообщение "Принята сумма 2 руб.";

w ₃- выдача газеты;

w ₄ - возврат денег.

Состояния автомата:

s ₀ - принята сумма 0 руб. (начальное состояние);

s ₁ - принята сумма 1 руб.;

s ₂ - принята сумма 2 руб.

Функцию переходов представим таблицей 1, а функцию выходов - таблицей 2.

Этот же автомат можно задать в виде отмеченного орграфа, вершины которого соответствуют состояниям автомата, а дуги - переходам (рис.1).

Ниже приведен пример реакции автомата ПРОДАВЕЦ на входную последовательность v ₁ v ₁ v ₂ v ₂ v ₁ v ₂ v ₂ v ₁ v ₁ v ₁…:

t

…

v(t)

…

v1

v1

v2

v2

v1

v2

v2

v1

v1

v1

…

s(t)

…

s0

s1

s2

s0

s2

s0

s2

s0

s1

s2

s0

w(t)

…

w1

w2

w4

w2

w3

w2

w4

w1

w2

w3

…

Автомат Мура

Абстрактный автомат Мура это частный случай автомата Мили (4), когда выходной символ зависти только от состояния автомата, а именно функция выходов автомата Мура:

w = m (s) (5)

Для каждого автомата Мили можно построить эквивалентный автомат Мура, реализующий точно такой же алфавитный оператор. Пусть A = < V,W,S,l,m,s (0)> автомат Мили. В качестве состояний эквивалентного автомата Мура возьмем пары . Тогда функция выходов эквивалентного автомата Мура

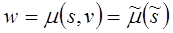, (6)

а функция переходов

. (7)

Пример 2. Для рассмотренного выше автомата ПРОДАВЕЦ можно построить эквивалентный автомат Мура, характеризуемый таблицей переходов/выходов (табл 3).

Таблица 3

Новое состояние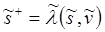
Входной символ	Текущее состояние/выходной символ
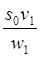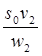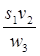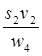
v 1 v 2	s 1 v 1 s 2 v 1 s 2 v 1 s 0 v 1 s 0 v 1 s 0 v 1 s 1 v 2 s 2 v 2 s 2 v 2 s 0 v 2 s 0 v 2 s 0 v 2

На рис.3 представлен граф переходов/выходов автомата ПРОДАВЕЦ, соответствующий табл.3. Начальное состояние эквивалентного автомата Мура включает входной символ v (0). Поэтому приходится смещать поток входных символов: .

Пример 3. Обозначим состояние автомата Мура, соответствующее паре (s _i, v _j) автомата Мили через s _ij. Тогда реакция эквивалентно автомата ПРОДАВЕЦ на последовательность v ₁ v ₁ v ₂ v ₂ v ₁ v ₂ v ₂ v ₁ v ₁ v ₁… будет:

t	…
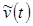
	…	v 1	v 2	v 2	v 1	v 2	v 2	v 1	v 1	v 1	…
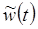
	…	s 01	s 11	s 12	s 02	s 21	s 02	s 22	s 01	s 11	s 21
w(t)	…	w 1	w 2	w 4	w 2	w 3	w 2	w 4	w 1	w 2	…

Дата добавления: 2015-10-23