Нелинейные модели регрессии

Основные определения и формулы

Нелинейные модели регрессии

Между экономическими явлениями существуют не только линейные, но и нелинейные соотношения, которые выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;

• регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:

• полиномы разных степеней

y =a ₀ + a ₁ ∙x ₁ + a ₂ ∙x ₂² + u,

y = a ₀ + a ₁ ∙x ₁ + a ₂ ∙x ₂² + a ₃ ∙x ₃³ + v;

• равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

• степенная

у = а ₀ ∙х^a1∙u;

• показательная

у = а ₀ ∙a ₁ ^x u;

• экспоненциальная

.

• кинематическая функция (функция Перла — Рида)

• функция Джонсона

При оценивании регрессионных моделей

y = f(x;a) + u

Е (и|х) = 0, σ ²(и | х) = σ ² _и

с нелинейными по коэффициентам функциями регрессии, такими, как приведены выше, не удается непосредственно воспользоваться статистическими процедурами оценки параметров, созданными для линейных регрессионных моделей.

Модели, нелинейные по переменным. В моделях, нелинейных по переменным, регрессоры, имеющие степень отличную от первой, заменяются другими независимыми переменными первой степени, и к полученной модели с новыми переменными применяется обычный МНК.

Нелинейная регрессия по включенным переменным не имеет сложностей при оценке ее параметров. Они, как и в линейной регрессии, определяются методом наименьших квадратов (МНК), так как эти функции линейны по параметрам. Так, в параболе второй степени

y =a ₀ + a ₁ ∙x ₁ + a ₂ ∙x ₂² + u,

можно произвести замену переменных, например: z ₁ =х ₁ ,z ₂ =х ₂², и получим уравнение линейной регрессии вида:

y =a ₀ + a ₁ ∙z ₁ + a ₂ ∙z ₂ + u,

для оценки параметров которого, используется МНК.

Соответственно для полинома третьего порядка

y=a ₀ + a ₁ ∙x ₁ + a ₂ ∙x ₂² + a ₃ ∙x ₃³ + v;

при замене z ₁ =х ₁, x ₂ =х ₂², z ₃ =х ₃³ получим трехфакторную модель линейной регрессии:

y = a ₀ + a ₁ ∙z ₁ + a ₂ ∙z ₂ + a ₃ ∙z ₃ + v;

а для полинома k -го порядка

y=a ₀ + a ₁ ∙x ₁ + a ₂ ∙x ₂² + a ₃ ∙x ₃³ +….+ а_к∙x_k^k + v,

будет получена линейную модель множественной регрессии с к объясняющими переменными:

y = a ₀ + a ₁ ∙z ₁ + a ₂ ∙z ₂ + a ₃ ∙z ₃ +….+ а_к∙z_k + v;

Таким образом, полином любого порядка сводится к модели линейной множественной регрессии с ее методами оценивания параметров и проверки гипотез теоремы Гауса-Маркова. Опыт большинства исследователей отмечают, что среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени и, в отдельных случаях, полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.

Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений[1];

∑у =п∙а ₀ +а ₁ ∙∑х+ а ₂ ∙∑х ²,

∑у∙x =а ₀ ∙∑х+ а ₁ ∙∑х ² + а ₂ ∙∑х ³

∑у∙x ² =а ₀ ∙∑x ² + а ₁ ∙∑х ³ + а ₂ ∙∑х ⁴

Для преобразования гиперболической регрессии (обратная модель)

к линейному виду используется замена: .

Модели, нелинейные по параметрам. В моделях, нелинейных по параметрам, например степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является их линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование.

Рассмотрим процесс логарифмирования на примере нелинейной по параметрам парной регрессии вида

y = a ₀ ∙x^a1, (1.1)

где a ₀ и a₁ - параметры модели. Параметр a данной степенной модели представляет собой значение эндогенной переменной, полученное при единичном значении регрессора. Для того чтобы дать экономическую интерпретацию параметру a ₁ данной модели, продифференцируем данное уравнение по переменной x:

тогда

параметр a ₁ представляет собой эластичность переменной y по переменной x. Уравнение (1.1) не является линейным. Прологарифмируем обе части данного уравнения:

ln (y) = ln (a ₀) + a₁ ln (x) = A₀ + a₁∙z, (1.2)

где

A₀ = ln (a ₀), z = ln (x).

Спецификация (1.2) называется двойной логарифмической моделью [2], так как и эндогенная переменная, и регрессор используются в логарифмической форме. Второе название модели — модель с постоянной эластичностью — следует из того факта, что параметр a ₁, являясь константой, представляет собой эластичность.

Уравнение (1.2) линейно относительно логарифмов переменных, потому, вводя обозначения:

Y=ln (y)

получаем спецификацию линейной модели, к которой при соответствующем включении случайного возмущения применим МНК:

Y = A + a ₁ ∙z + u (1.3)

Модели типа (1.2) используются в микроэкономике для построения производственных функций, функций потребления, функций спроса и т.д.

Спецификации линейных моделей, включающих или только логарифмы значений эндогенной переменной, или только логарифмы значений регрессора, называются полулогарифмическими. Так модель со спецификацией вида:

ln (y) = a + a ₁ ∙x + u (1.4)

относится к полулогарифмическим моделям и называется лог-линейной моделью. Для преобразования данной модели к линейному виду следует произвести замену Y = ln (y).

Полулогарифмические модели обычно используются для измерения темпа прироста экономических переменных.

Следующий тип полулогарифмических моделей получил название — линейно-логарифмическая модель:

Полулогарифмическая модель вида

y= a ₀ + a ₁ ∙ln (x)+ u (1.5)

называется линейно-логарифмической моделью, которая приводится к линейной путем замены X = ln (x). Получаем модель вида

y= a ₀ + a ₁ ∙X + u (1.6)

Модель (1.5) используется при исследовании влияния процентного изменения регрессора на абсолютное изменение эндогенной переменной, например, при моделировании влияния процентного изменения денежной массы на изменение объема ВНП.

Способ включения случайного возмущения. Случайные возмущения в линейных регрессионных моделях должны удовлетворять условиям Гаусса—Маркова, только в этом случае МНК - оценки будут состоятельными, несмещенными и эффективными. Поэтому при линеаризации нелинейных регрессионных моделей важным этапом является этап включения случайного возмущения в исходное уравнение, оно также будет подвержено определенному преобразованию.

В нелинейных по переменным моделях случайное возмущение является аддитивным и не подвергается никакому преобразованию при линеаризации. В моделях логарифмического типа для линеаризации исходных нелинейных уравнений регрессии используется операция логарифмирования. Этому же преобразованию подвергается и случайное возмущение. Для того, чтобы в линейное уравнение после линеаризации возмущение входило аддитивно, в исходную нелинейную спецификацию оно должно включаться мультипликативно, изменяя значение эндогенной переменной в некоторой случайной пропорции.

Для модели (1.1) возможны следующие способы включения случайного возмущения:

y = a ₀ ∙x^{a 1} ∙u (1.6)

y = a ₀ ∙x ^{a 1} ∙u^ε (1.7)

y = a ₀ ∙x ^{a 1} +u (1.8)

где u, ε — случайные возмущения. Линеаризуем перечисленные выше регрессионные модели путем логарифмирования. Первая модель (1.6) преобразуется в парную логарифмическую модель вида:

ln (y) = A ₀ + a ₁ ln (x) + v

где A ₀ =ln (a ₀).

Случайное возмущение v = ln (u) включено в линейную спецификацию аддитивно. Чтобы оно удовлетворяло условиям нормальной линейной регрессионной модели, возмущение v исходной нелинейной спецификации (1.6) должно иметь логарифмическое нормальное распределение.

Значение е = ln (v) = 0, при v = 1, что не приводит к изменениям значений эндогенной переменной в спецификации (1.6).

Линеаризация спецификации (1.7) также приводит к линейной модели вида:

ln (y) = A ₀ + a₁ ln (x) + е,

e = ε∙ ln (u)

но случайное возмущение е имеет нормальное распределение с параметрами

E(e) = 0, Var (e) = σ²,

а не логарифмически нормальное, как в предыдущем случае. Поэтому применение МНК не вызывает затруднений. Значение е = 0 не приводит к изменениям значений эндогенной переменной в спецификации (1.7).

Логарифмическое преобразование нелинейной спецификации (1.8) с аддитивным случайным возмущением не приводит к линейной модели:

ln (y) = ln (a ₀ ∙x ^{a 1} +u),

поэтому непосредственное применение обычного МНК в данном случае невозможно. Для оценки параметров таких нелинейных моделей разработан нелинейный метод наименьших квадратов, основные положения которого приведены в [1, стр. 418].

Таблица 1

Коэффициенты эластичности для ряда математических функций

Вид функции y	Первая производная,	Коэффициент эластичности,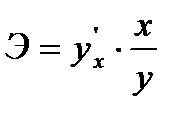
Линейная y = a 0 + a 1∙ x + u	a 1
Парабола второго порядка y = a 0 + a 1∙ x + a 2∙ x ^2 + u	a 1∙+2∙ a 2∙ x
Гипербола
Показательная
Степенная		Э = a 1
Полулогарифмическая y = a 0 + a 1∙ln x + u
Логистическая
Обратная

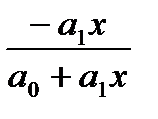
Внимание. После того, как будет получено уравнение с оцененными параметрами, введенные в него новые независимые переменные заменяются на первоначальные.

См. дополнительно литературу: [1, с. 178 - 199]; [2, с. 331 -346]; [5, с. 124 - 127; [7, с.62-80] [10]; [11].

2. Пример: «Как повысить производительность труда сотрудников Компании»

Генеральный директор фирмы «Морозко», выпускающей холодильники, на основании бенчмаркинга, подготовленного аналитическим отделом, пришёл к выводы, что производительность работы служащих фирмы должна быть существенно повышена. В нашем случае объектом исследования являются совокупность предприятий, выпускающих аналогичную продукцию. Результирующим показателем является y - производительность труда (тыс. руб./чел).

Необходимо определить основные показатели (значащие факторы), влияющие на производительность труда, собрать и обработать статистические данные, построить эконометрическую модель, оценить её параметры, качество и адекватность, определить наиболее существенные показатели, на которые можно и целесообразно воздействовать, чтобы повысить производительность труда и доход фирмы.

Предлагаются следующие экономические показатели, см. кейс 3:

y - з ависимый фактор (объясняемая переменная): производительность труда, (тыс. руб. / чел).

В результате дискуссии в аналитическом центре компании были выбраны независимые факторы, которые могли влиять на производительность труда сотрудников компании:

Независимые факторы (потенциальные объясняющие переменные):

x ₁ – стоимость сырья и материалов (тыс. руб.)

x ₂ – заработная плата (тыс. руб.)

x ₃ – основные промышленно-производственные фонды (тыс. руб.)

x ₄ – расходы на переподготовку и повышение квалификации сотрудников (тыс. руб.)

x ₅ – расходы на модернизацию производства (тыс. руб.)

x ₆ – расходы на электроэнергию (тыс. кВт час.)

Численные значения переменных представлены в таблице 2.1.

Таблица 2.1.

№ объекта наблюдения	y	x 1	x 2	x 3	x 4	x 5	x 6
	10,4						4,2
	19,7						13,3
	17,7
	17,5						5,6
	13,1						4,1
	14,4						7,3
	15,1						8,7
	11,9						1,9
	13,9						10,1
	19,5
	14,5						9,2
	12,5						9,8
	19,8						11,6

Занятие 1

Рассмотрим следующую нелинейную эконометрическую модель, представленную полиномом вида:

y= a ₀ + a ₁ x ₁²+ a ₂ x ₂² + a ₃ x ₃² + a ₄ x ₄²+ a ₅ x ₅²+ a ₆ x ₆² + u

При проведении работы следует:

1. Определить форму связи между переменными х и у.

2. Оценить параметры нелинейной множественной регрессии, предполагая, что соблюдаются условия теоремы Гауса-Маркова.

3. Построить график исходной модели и на него «наложить» график полученной парной регрессии.

4. Построить график остатков полученной нелинейной множественной регрессии и по нему определить их характер.

5. Проверить выполнение отдельных условий теоремы Гауса-Маркова: проверить остатки на гомоскедастичность и на автокорреляцию.

6. Оценить тесноту связи между переменными х и у, используя для этого показатели корреляции и детерминации.

7. Оценить с помощью средней ошибки аппроксимации качество полученной регрессии, т.е. отклонение расчетных значений от фактических.

8. Оценить статистическую надежность результатов по полученной регрессии с помощью F – критерия Фишера.

9. Оценить качество полученных параметров нелинейной множественной регрессии.

10. Определить доверительный интервал прогноза для уровня значимости α = 0,5 и проверить полученные параметры регрессии на адекватность.

11. Определить доверительный интервал прогноза для уровня значимости α = 0,5 и проверить полученную регрессию на адекватность.

12. Результаты проведенных исследований следует внести в отчет (см. Приложение 1).

Данную модель следует привести к линейной, т.е. провести линеаризацию нелинейной множественной регрессии. Сделать это можно путем замены переменных. Введем следующие переменные:

z 1 = x ₁², z ₂ = х ₂², z ₃ = х ₃², z ₄ = x ₄², z ₅ = х ₅², z ₆ = x ₆²,

и пересчитаем исходные значения нелинейной эконометрической модели, см. табл. 2.2.

Таблица 2.2.

№ объекта наблюдения	y	z 1	z 2	z 3	z 4	z 5	z 6
	10,4						17,64
	19,7						176,89
	17,7
	17,5						31,36
	13,1						16,81
	14,4						53,29
	15,1						75,69
	11,9			1,06E+08			3,61
	13,9						102,01
	19,5			1,57E+08
	14,5						84,64
	12,5						96,04
	19,8						134,56

После замены переменных получаем уже линейную множественную эконометрическую модель вида

y= a ₀ + a ₁ z ₁ + a ₂ z ₂ + a ₃ z ₃+ a ₄ z ₄+ a ₅ z ₅+ a ₆ z ₆ + u

Все последующие операции проводим с полученными данными: тест Дарбина-Уотсона, тест Голдфелда-Квандта, F-тест, t-тест.

(данные процедуры были подробно рассмотрены в кейсе 3, а поэтому здесь не приводятся)

Проведите необходимые исследования самостоятельно.

В результате получены следующие значения параметров:

a ₀ = 12,03266 a ₁ = 4,43E-08 a ₂ = 4,48E-06 a ₃ = -2,4E-08

a ₄ = -0,00053 a ₅ = 9,82E-06 a ₆ = 0,013924

Множественный R =0,813 R-квадрат = 0,660

Стандартная ошибка = 2,60

ta ₀ = 6,375374 ta ₁ = 1,030028 ta ₂ = 0,680882 ta ₃ = -0,93393

ta ₄ = -0,56102 ta ₅ = 0,769213 ta ₆ = 0,542287

Получена следующая нелинейная множественная регрессия

y=12,0327+4,43E-08 z ₁+4,48E-06 z ₂-2,4E-08 z ₃-0,0005 z ₄+9,82E-06 z ₅+0,0139 z ₆

(1,887) (4,3E-08) (6,58E-06) (2,56E-08) (0,0009) (1,28E-05) (0,0256)

Ниже представлены графики остатков рассматриваемой множественной модели для проведения их оценки на гомоскедастичность:

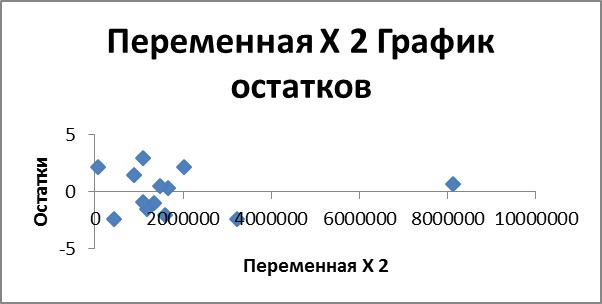
Проведем проверку полученной нелинейной множественной регрессии на адекватность.

Для этого следует определить количество наблюдений в учебной и контролирующей выборках. Провести оценку параметров исходной модели по учебной выборке. Оценить значение объясняемой переменной по полученным оценочным параметрам учебной выборки. Определить интервальные значения для проверки имеющихся значений объясняемой переменной из контролирующей выборки. Определить попадает ли в рассчитанный интервал значения объясняемой переменной из контролирующей выборки.

(данную процедуру студенты должны выполнить самостоятельно, на основании полученных практических знаний в кейсе 3)

Внимание. Для задачи, выбранной в качестве самостоятельной работы, проведите анализ нелинейной эконометрической модели, представленной полиномиальной функцией. Результаты проведенного исследования запишите в отчет.

Занятие 2

Рассмотрим нелинейную эконометрическую модель, представленную степенной функцией:

y= a ₀∙ x ₁ ^{a 1}∙ x ₂ ^{a 2}∙ x ₃ ^{a 3}∙ x ₄ ^{a 4}∙ x ₅ ^{a 5}∙ x ₆ ^{a 6}∙ u

Исходные данные выбираются из таблицы 2.1

Данную модель следует привести к линейной, т.е. провести ее линеаризацию. Сделать это можно путем логарифмирования исходных данных и переобозначения переменных:

lny = lna ₀+ a ₁∙ lnx ₁ + a ₂∙ lnx ₂ + a ₃∙ lnx ₃ + a ₄∙ lnx ₄ + a ₅∙ lnx ₅ + a ₆∙ lnx ₆ + lnu

Введем следующие переменные:

Y= lny, A₀ = lna ₀, z ₁ = lnx ₁, z ₂ = lnx ₂, z ₃ = lnx ₃,

z ₄∙= lnx ₄, z ₅ = lnx ₅, z ₆ = lnx ₆, e = lnu

и пересчитаем исходные значения нелинейной эконометрической модели, см. табл. 2.3.

Таблица 2.3.

№ объекта наблюдения	Y	z 1	z 2	z 3	z 4	z 5	z 6
	2,342	6,763	6,479	7,874	3,989	5,106	1,435
	2,981	9,166	7,160	9,117	4,654	5,869	2,588
	2,874	7,196	6,953	8,021	4,443	5,991	1,386
	2,862	8,846	6,850	7,845	4,369	5,743	1,723
	2,573	8,395	6,988	8,316	4,522	5,832	1,411
	2,667	8,447	7,139	8,767	4,654	6,207	1,988
	2,715	7,650	7,100	8,486	4,615	5,576	2,163
	2,477	7,102	5,537	9,240	2,944	4,357	0,642
	2,632	8,555	7,493	9,170	5,011	5,927	2,313
	2,970	8,510	7,955	9,437	5,481	6,001	2,485
	2,674	7,634	7,053	8,813	4,564	6,133	2,219
	2,526	7,724	6,947	8,842	4,635	6,045	2,282
	2,986	8,074	7,259	8,046	4,836	6,295	2,451

После замены переменных получаем уже линейную множественную эконометрическую модель вида

Y= A ₀ + a ₁ z ₁ + a ₂ z ₂ + a ₃ z ₃+ a ₄ z ₄+ a ₅ z ₅+ a ₆ z ₆ + e

Все последующие операции проводим с полученными данными: тест Дарбина-Уотсона, тест Голдфелда-Квандта, F-тест, t-тест.

(данные процедуры были подробно рассмотрены в кейсе 3, а поэтому здесь не приводятся)

Проведите необходимые исследования самостоятельно.

В результате получены следующие значения параметров:

А ₀ = -2,6258 a ₁ = 0,0773 a ₂ = 1,6972 a ₃ = -0,0756

a ₄ = -1,6819 a ₅ = 0,1386 a ₆ = 0,1550

Множественный R =0,776 R-квадрат = 0,603

Стандартная ошибка = 0,1854

tА ₀ = -0,8049 ta ₁ = 0,0982 ta ₂ = 1,4516 ta ₃ = -0,6428

ta ₄ = -1,3982 ta ₅ = 0,6102 ta ₆ = 0,7688

Для перехода к исходной нелинейной множественной регрессии пересчитаем значение а ₀

a ₀= e^A0 = e^-2,6258 = 0,072381

Таким образом, нелинейная множественная регрессия будет иметь вид:

y= 0,0724 ∙ x ₁^0,077 ∙ x ₂^1,697 ∙ x ₃^-0,076 ∙ x ₄^-1,682 ∙ x ₅^0,139 ∙ x ₆^0,155

(3,267) (0,098) (1,169) (0,118) (1,203) (0,227) (0,202)

Ниже представлены графики остатков рассматриваемой множественной модели для проведения их оценки на гомоскедастичность:

Проведем проверку полученной нелинейной множественной регрессии на адекватность.

Для этого следует определить количество наблюдений в учебной и контролирующей выборках. Провести оценку параметров исходной модели по учебной выборке. Оценить значение объясняемой переменной по полученным оценочным параметрам учебной выборки. Определить интервальные значения для проверки имеющихся значений объясняемой переменной из контролирующей выборки. Определить попадает ли в рассчитанный интервал значения объясняемой переменной из контролирующей выборки.

(данную процедуру студенты должны выполнить самостоятельно, на основании полученных практических знаний в кейсе 3)

Внимание. Для задачи, выбранной в качестве самостоятельной работы, проведите анализ нелинейной эконометрической модели, представленной степенной функцией. Результаты проведенного исследования запишите в отчет.

Занятие 3

Рассмотрим нелинейную эконометрическую модель, представленную показательной функцией:

y= a ₀∙ a ₁ ^{x 1}∙ a ₂ ^{x 2}∙ a ₃ ^{x 3}∙ a ₄ ^{x 4}∙ a ₅ ^{x 5}∙ a ₆ ^{x 6}∙ u

Исходные данные выбираются из таблицы 2.1

Для линеаризации данной нелинейной множественной модели проведем логарифмирования исходных данных и переобозначим переменные:

lny = lna ₀+ x ₁∙ lna ₁ + x ₂∙ lna ₂+ x ₃∙ lna ₃ + x ₄∙ lna ₄ + x ₅∙ lna ₅ + x ₆∙ lna ₆ + lnu

Введем следующие переменные:

Y= lny, A₀ = lna ₀, A₁ = lna ₁, A₂ = lna ₂, A₃ = lna ₃,

A₄ = lna ₄, A₅ = lna ₅, A₆ = lna ₆, е = lnu

и пересчитаем исходные значения нелинейной эконометрической модели, см. табл. 2.4.

Таблица 2.4.

№ объекта наблюдения	Y	x 1	x 2	x 3	x 4	x 5	x 6
	2,342						4,2
	2,981						13,3
	2,874
	2,862						5,6
	2,573						4,1
	2,667						7,3
	2,715						8,7
	2,477						1,9
	2,632						10,1
	2,970
	2,674						9,2
	2,526						9,8
	2,986						11,6

После замены переменных получаем уже линейную множественную эконометрическую модель вида

Y= A ₀ + A ₁ x ₁+ A ₂ x ₂ + A ₃ x ₃ + A ₄ x ₄ + A ₅ x ₅ + A ₆ x ₆ + e

Все последующие операции проводим с полученными данными: тест Дарбина-Уотсона, тест Голдфелда-Квандта, F-тест, t-тест.

(данные процедуры были подробно рассмотрены в кейсе 3, а поэтому здесь не приводятся)

Проведите необходимые исследования самостоятельно.

В результате получены следующие значения параметров:

А ₀ = 2,3449 А ₁ = 2,13E-05 А ₂ = 0,0010 А ₃ = -1,4E-05

А ₄ = -0,0114 А ₅ = 0,0004 А ₆ = 0,0167

Множественный R =0,787 R-квадрат = 0,6199

Стандартная ошибка = 0,1813

tА ₀ = 11,73408 tА ₁ = 0,814211 tА ₂ = 1,012574 tА ₃ = -0,6572

tА ₄ = -0,90562 tА ₅ = 0,666479 tА ₆ = 0,623158

Для перехода к исходной нелинейной множественной регрессии пересчитаем значение а ₀

a ₀= e^A0 = e^2,3449 = 10,433

a ₁= e^A1 = e^2,13E-05 = 1,000

a ₂= e^A2 = e^0,0010 = 1,001

a ₃= e^A3 = e^-1,4E-05 = 0,999

a ₄= e^A4 = e^-0,0114 = 0,989

a ₅= e^A5 = e^0,0004 = 1,000

a ₆= e^A6 = e^0,0167 = 1,017

Таким образом, нелинейная множественная регрессия будет иметь вид:

y= 10,433 ∙ 1,000 ^{x 1} ∙ 1,001 ^{x 2} ∙ 0,999 ^{x 3} ∙ 0,989 ^{x 4} ∙ 1,000 ^{x 5} ∙ 1,017 ^{x 6}

(0,1998) (2,62E-05) (0,0010) (2,14E-05) (0,0127) (0,0006) (0,0267)

Ниже представлены графики остатков рассматриваемой множественной модели для проведения оценки их на гомоскедастичность:

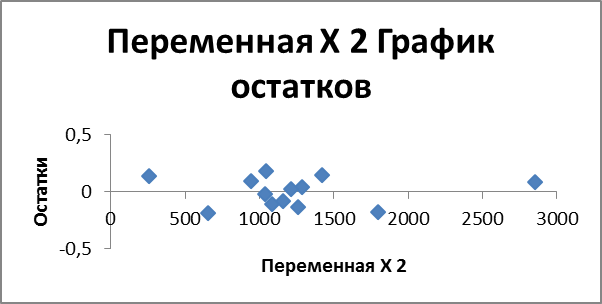
Проведем проверку полученной нелинейной множественной регрессии на адекватность.

Для этого следует определить количество наблюдений в учебной и контролирующей выборках. Провести оценку параметров исходной модели по учебной выборке. Оценить значение объясняемой переменной по полученным оценочным параметрам учебной выборки. Определить интервальные значения для проверки имеющихся значений объясняемой переменной из контролирующей выборки. Определить попадает ли в рассчитанный интервал значения объясняемой переменной из контролирующей выборки.

(данную процедуру студенты должны выполнить самостоятельно, на основании полученных практических знаний в кейсе 3)

Внимание. Для задачи, выбранной в качестве самостоятельной работы, проведите анализ нелинейной эконометрической модели, представленной показательной функцией. Результаты проведенного исследования запишите в отчет.

Дата добавления: 2015-10-23