Отметьте неверный ответ.

Закон Гука для стержня имеет вид:

+:

- В предположении, что при повышении температуры на 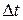и под действием силы F зазор закроется, уравнение совместности деформаций имеет вид:

+:

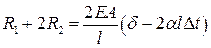
- Внутренняя продольная сила в указанном сечении определяется по формуле:

+:

- Напряжение в поперечных сечениях стержня при изменении температуры на 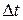определяется по формуле:

+:

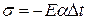
- После установки (монтажа) стержня между неподатливыми стенками, напряжения в поперечных сечениях вычисляются по формуле:

+:

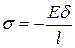
- Данная стержневая конструкция (1 и 2 - упругие элементы; АВ абсолютно жесткий элемент) является:

+: статически определима

- В растянутом и сжатом стержне максимальные касательные напряжения действуют …

+: на площадках под углом в 45⁰ к оси стержня

- При растяжении или сжатии стержня максимальные нормальные напряжения действуют…

+: в поперечных сечениях

- В поперечных сечениях стержневых элементов статически неопределимых конструкций не могут действовать…

+: касательные напряжения

- Дополнительные уравнения при расчете статически неопределимых стержневых конструкций составляются…

+: как соотношения между деформациями стержневых элементов при условии сохранения их неразрывности

- Коэффициент Пуассона это упругая характеристика материала и …

+: представляет модуль отношения относительной и поперечной деформаций

(на самом деле модуль отношения относительной продольной и поперечной деформаций, но отвечать надо так)

- Накопленная потенциальная энергия деформации стержня вычисляется по формуле:

+:

- При решении некоторых задач на растяжение-сжатие необходимо учитывать, что:

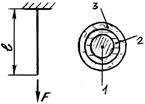- Стержень имеет указанное строение. Внутренняя продольная сила распределяется между частями стержня в следующей пропорции:

+:

- Чугунный образец при испытаниях на сжатие разрушается по форме

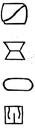+: 1) 1)

2)

3)

4)

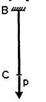- Пусть - допускаемые перемещения сечения С при растяжении и сжатии, - абсолютное удлинение- укорочение стержня ВС.

Тогда проверку на жесткость стержня ВС проводят по условию…

+:

- В вопросах на кручение в тестах крутящий момент обозначен Т (мы обозначали ).

- А – площадь поперечного сечения тела заклепки, 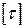- допускаемое напряжение на срез. Допускаемое значение силы F определяется по формуле…

+:

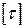- Если - допускаемое касательное напряжение, то из расчета на прочность, скручивающий момент…

+:

(В правильном ответе пропущена буква 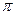перед d)

- Как должен изменяться диаметр вала, если передаваемая им мощность Р остается без изменения, а угловая скорость ω увеличивается?

+: 1 уменьшаться

- Какую максимальную мощность может передать вал диаметром d=100мм без нарушения прочности, если допускается напряжение τ_adm=50 МПа и угловая скорость вращения ω=80 с^-1?

+: 800 кВт

- Записать уравнение для определения прогиба балки при плоском изгибе ( - знак обобщенной функции):

+:

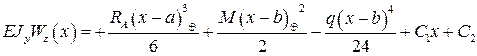
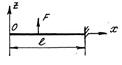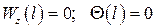
- Какие граничные условия необходимо поставить для балки при плоском изгибе:

+:

- Какие граничные условия необходимо поставить для балки при плоском изгибе:

+:

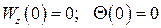
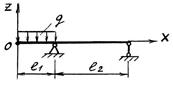- Какие граничные условия необходимо поставить для балки при плоском поперечном изгибе:

+:

- Подсчитать величину обобщенной функции при x = 4:

+: y= 8

(при вычислении обобщенной функции скобка с плюсиком равна нулю, если она отрицательна. Например, в данном случае: у(5)=4+4+0+0=8)

- Определить касательное напряжение в точке 2, где ширина сечения равна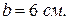

Дано: .

+:

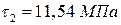
- Записать уравнение для обобщенного момента при плоском поперечном изгибе для балки:

+:

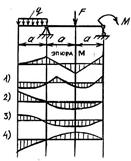Согласно эпюре М наиболее вероятным является вид упругой линии (изогнутой оси) балки:

+: 3)

- Полный расчет балки при плоском изгибе не требует выполнения:

+: условия продольной устойчивости

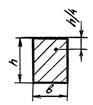
- Чему равно касательное напряжение в точке А прямоугольного сечения балки при изгибе, если в этом сечении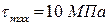

+:

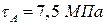
- При чистом изгибе стержня главные площадки в окрестности точки К совпадают…

+: с поперечным и двумя продольными сечениями стержня

- вид нагружения бруса, когда в поперечном сечении бруса одновременно действуют несколько внутренних усилий, называется:

+: сложным сопротивлением

- для определения напряжений при сложном сопротивлении используется:

+: принцип суперпозиции

- пространственный изгиб вызывается:

+: моментами, расположенными в разных плоскостях, проходящих через ось балки

- вид пространственного изгиба, когда нагрузки лежат в одной плоскости, не совпадающей ни с одной из главных плоскостей, называется:

+: косым изгибом

- если, при действии нескольких изгибающих моментов, J_y=J_z, то имеет место:

+: плоский изгиб

- направление полного прогиба при косом изгибе

+: перпендикулярно нейтральной линии

- полный прогиб при неплоском изгибе определяется как

+:

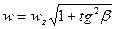
положение нулевой линии при внецентренном изгибе зависит от

+: положения полюса и геометрии сечения

(видимо, имелось в виду при внецентренном растяжении)

выберите правильный вариант ответа

- ядром сечения называется область вокруг центра тяжести поперечного сечения, которая обладает следующим свойством:

+:если нагрузка расположена в области ядра, то нормальные напряжения во всех точках поперечного сечения имеют один знак

- при повороте нейтральной линии вокруг фиксированной точки контура сечения

+: точка приложения силы перемещается вдоль некоторой прямой

- при расчете на прочность при изгибе с кручением используется

+: определенная теория прочности

- эквивалентные напряжения при изгибе с кручением по третьей теории прочности

+:

- вид сложного сопротивления представляет собой

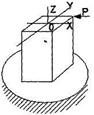+: изгиб с кручением

- как расположены полюс и нейтральная линия (N-N) при внецентренном сжатии

+: по разные стороны от центра тяжести

- если полюс при внецентренном сжатии лежит на одной из главных осей сечения, то нейтральная линия N-N

+: параллельна другой главной оси

- при изгибе с кручением имеет место …………… напряженное состояние

+: плоское

- условие прочности по третьей теории прочности при изгибе с кручением для круглых брусьев имеет вид

+:

- условие прочности по четвертой теории прочности при изгибе с кручением для круглых брусьев имеет вид

+:

- при косом изгибе для прямоугольного сечения (h x b)

+:

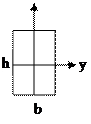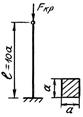- Определить критическую силу по формуле Эйлера. Сечение стержня квадрат со стороной а:

+:

(Формула Эйлера имеет вид: ; здесь ; )

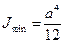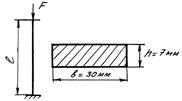
- Определить: 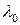- предельную гибкость стержня; - величину критической силы

+:

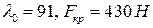
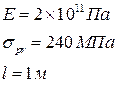
(здесь , т.к. один конец стержня свободен, а второй защемлён; 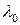вычисляется по формуле ; вычисляется по формуле . Т.к. , то применяется формула Эйлера =430 Н; Если бы оказалось, что 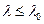, то использовалась бы формула Ясинского: )

- Определить величину критической силы для сжатой стойки квадратного сечения со стороной а. Оба конца шарнирно-оперты.

+:

(необходимо учитывать, что в случае, когда оба конца шарнирно-оперты )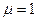

- Записать формулу для определения гибкости стержня:

+:

- Предельная гибкость стержня зависит только от:

+: материала, из которого изготовлен стержень

- Признаком потери устойчивости сжатого стержня является…

+: внезапная смена прямолинейной формы равновесия на криволинейную

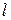- при изменении и 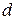величина критического напряжения 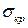будет изменяться пропорционально отношению:

+:

- Для определения критической нагрузки за пределом пропорциональности используется формула:

+: Ясинского

- Определить (гибкость стержня), если , .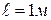

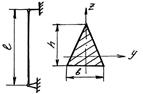
+: 163

- Коэффициент приведенный длины стержня 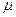при вычислении критической силы по формуле Эйлера зависит:

+: способа закрепления стержня

(оба конца шарнирно-оперты ;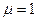

оба конца защемлены ;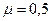

один конец свободен, а второй защемлён ;

один конец шарнирно-оперт, а второй защемлён )

- Формула Ясинского применима, если …

+: критическое напряжение 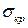превышает предел пропорциональности

- В формуле Ясинского входит параметр …

+: гибкость

- Условие применимости формулы Эйлера имеет вид…

+:

Дата добавления: 2015-10-23