
|
Читайте также: |
Можно попробовать использовать для хранения данных таблицу без ссылок. Будем дополнительно в каждой ячейке таблицы хранить информацию о том – занята ли ячейка или нет. Если при занесении в таблицу нового элемента хэш-функция от заносимого значения укажет на пустую ячейку, то проблем никаких нет. Иначе, получается ситуация, называемая коллизией. Разрешение коллизий является основной целью при создании алгоритмов работы с хэшируемыми множествами.
Простейший способ разрешения коллизий в таблице следующий: если элемент, на который указывает хэш-функция, занят, то мы рассматриваем последовательно все элементы таблицы от текущего, пока не найдем свободной место. Новый элемент помещается в найденное свободное место. Чтобы отследить ситуацию с переполнением таблицы, мы введем переменную M – счетчик количества занятых ячеек в таблице. Если значение M достигло величины N-1, то мы считаем, что наступило переполнение. Это гарантирует нам, что в таблице всегда будет в наличии хотя бы одна пустая позиция.
При таком способе разрешения коллизий для поиска элемента x в таблице требуется вычислить хэш-функцию от значения элемента h(x). Если позиция с номером h(x) пуста, то элемент x в таблице отсутствует. Иначе перебираются элементы таблицы от позиции с номером h(x) до первой пустой позиции. Если среди этих элементов x найден не будет, то он отсутствует в таблице.
На языке С алгоритм поиска элемента value в таблице из Nmax целых чисел можно реализовать следующим образом.
#define Nmax 1000
typedef struct CNode_{int value; int is_empty;} CNode;
CNode node[Nmax];
Int hash(int value);
int search(CNode node[])
{
Int i;
for(i=hash(value);!node[i].is_empty; i=(i==0? Nmax-1: i-1))
if(node[i].value==value)return i;
return –1;
}
здесь hash(int value) – хэш-функция; член структуры is_empty равен нулю, если элемент пуст, единице – иначе. В данной реализации поиск идет по направлению уменьшения индекса. Наличие в таблице хотя бы одной пустой позиции гарантирует нам, что цикл не будет вечным.
Чтобы сэкономить память признаки пустоты элементов таблицы можно реализовать отдельно от самой таблицы. Тогда под каждую ячейку можно будет отвести ровно 1 бит информации:
#define Nmax 1000
int value[Nmax], is_empty[(Nmax+31)/32];
Int hash(int value);
int search(CNode node[])
{
Int i;
for(i=hash(value);!(is_empty[i/32]&(i%32)); i=(i==0? Nmax-1: i-1))
if(node[i].value==value)return i;
return –1;
}
Удаление элемента из таблицы несколько более сложное, чем добавление и поиск. Нельзя просто объявить позицию i, в которой требуется удалить элемент, пустой. Если это сделать, то элемент value[j] с индексом j<i, для которого h(value[j])>i и для которого все элементы с индексами между j и i заняты, окажется потерянными для последующего поиска (здесь мы рассматриваем случай отсутствия `перескока’ в конец массива при поиске очередного элемента). Действительно, при поиске этого элемента мы обязательно натолкнемся на пустую позицию value[i] и поиск будет завершен.
Чтобы исправить ситуацию мы должны найти первый такой элемент value[j], перенести его значение в позицию i и свести задачу к удалению элемента value[j]. Естественно, мы должны учитывать возможность `перескока’ в конец массива при поиске такого value[j]. Т.е., более строго, условия переноса value[j] в позицию i следующее:
h(value[j])>i>j (отсутствие перескока)
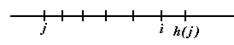
Или
j>h(value[j])>i (перескок)

Или
i>j>h(value[j]) (перескок)

Условием остановки алгоритма является пустота позиции j.
Подпрограмма удаления элемента с индексом i из списка может выглядеть следующим образом
void remove(CNode node[], int i)
{int j; node[i].is_empty=1;
for(j=i-1;!node[j].is_empty; j=(j==0? Nmax-1: j-1))
if((hash(value[j])>i && i>j) || (hash(value[j])>i && j>hash(value[j])) ||
(i>j && j>hash(value[j])))
{
node[i].is_empty=0; node[i].value=node[j].value;
Дата добавления: 2015-10-30; просмотров: 262 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Удаление вершины из B-дерева | | | Доказательство. |