Однопроходное добавление элемента в красно-черное дерево

Отметим, что красно-черные деревья имеют несколько худшую оценку высоты в зависимости от количества вершин в дереве, чем сбалансированные деревья. В реальной практике высоты деревьев различаются не существенно (имеется в виду – в среднем). Преимущество красно-черных деревьев является то, что добавление вершин может быть осуществлено за один проход по соответствующей ветви дерева. В сбалансированных деревьях требуется два прохода: один – для того, чтобы найти вершину, после которой следует вставить новую вершину, а второй – для балансировки дерева.

Итак, все, что нам нужно, это – не допустить реализации случая 1, т.к. случай 3 сводится к случаю 2, а последний завершает алгоритм. Это можно обеспечить, перекрашивая вершины при поиске листа, после которого следует вставить новую вершину. Иными словами, нам следует обеспечить, чтобы либо у вставляемой был бы черный родитель (тогда ничего больше делать не надо), либо у вставляемой вершины был бы черный дядя (тогда дерево можно сделать красно-черным за два поворота).

При поиске листа, после которого следует вставить новую вершину, вы, сначала рассматриваем в качестве текущей вершины p корень дерева. Далее в качестве p рассматриваем один из потомков корня, и т.д. Пусть, для определенности, от вершины p мы переходим к вершине p->left, тогда нам следует обеспечить, чтобы p->right была бы черной вершиной.

Рассмотрим все возможные случаи. Следует рассматривать только случаи, когда оба потомка p красные (легко увидеть, что случаи, когда p->left или p->right – черные нас устраивают).

1.p->par – черный, оба потомка p – красные. Тогда, все, что нужно сделать – перекрасить p и его потомков и перейти к рассмотрению следующей вершины p->left.

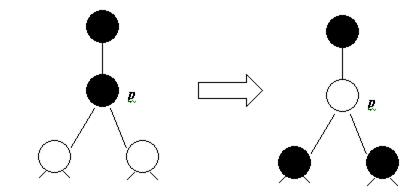
2.p->par – красный, причем p – правый потомок p->par, p->par – левый потомок p->par->par, оба потомка p – красные (случай, когда оба потомка – левые - аналогичен).

Сначала, мы перекрашиваем p и его потомков. Теперь мы попали в ситуацию, аналогичную случаю 2, рассмотренному выше. Как было показано выше, за один поворот и одну перекраску проблему можно решить.

3.p->par – красный, причем p – правый потомок p->par, p->par – левый потомок p->par->par, оба потомка p – красные (случай, когда p – левый потомок p->par, p->par – правый потомок p->par->par - аналогичен).

Сначала, мы перекрашиваем p и его потомков. Теперь мы попали в ситуацию, аналогичную случаю 3, рассмотренному выше. Как было показано выше, за два поворота и одну перекраску проблему можно решить.

Итак, мы показали, что алгоритм добавления вершины к красно-черному дереву можно реализовать за один проход по соответствующей ветви дерева.

Дата добавления: 2015-10-30