Добавление элемента в красно-черное дерево

Новая вершина вставляется в красно-черное дерева в два этапа.

На первом этапе вершина вставляется, как в обычное дерево поиска. Новая вершина красится в красный цвет. Следует отметить, что, в реальности фиктивных вершин может вообще не быть. Их наличие может обозначаться соответствующими нулевыми указателями у родительских вершин.

Добавление красной вершины x не меняет баланса дерева по черным вершинам.

Т.к. потомки новой вершины – фиктивные, то они – черные, по определению, что соответствует определению красно-черного дерева.

Единственная проблема, которая может возникнуть, это то, что у вставленной красной вершины x может оказаться красный родитель. Требуется изменить дерево, чтобы решить эту проблему.

При преобразованиях дерева мы будем сохранять указанное свойство: у нас будет сохраняться балансировка по черным вершинам и единственная возможная проблема это – некоторая красная вершина x будет иметь красного родителя.

Итак, x->par – красная, то x->par->par – черная (т.к. единственная проблема – нестыковка x->par и x, с другой стороны, у красной вершины может быть только черный родитель).

Будем называть вершину x->par->par->next, где next это – left или rightдядей вершины x, если x->par->par->next!= x->par.

Рассмотрим все возможные случаи.

1. Дядя вершины - x красный.

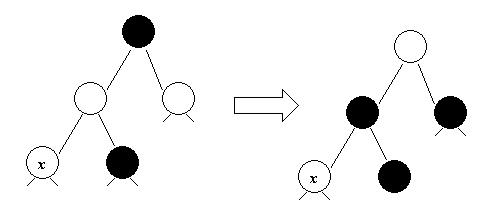
Перекрашиваем родителя, деда и дядю вершины x и рассматриваем в качестве вершины x ее деда: x=x->par->par.

Т.о. мы перенесли проблему выше по ветви дерева.

Осталось рассмотреть случаи, когда дядя вершины x - черный.

2. Дядя вершины - x черный, x – левый потомок x->par.

В этом случае мы проводим правый поворот x-b-a и в получившемся дереве перекрашиваем две вершины: a и b.

Вершина получившегося дерева – черная, проблем с цветами нет, баланс черного сохранился. Т.о. дерево сбалансировано. Последующая балансировка не требуется.

3. Дядя вершины - x черный, x – правый потомок x->par.

Делаем левый поворот f-x-b и ситуация сводится к предыдущему случаю.

4. У вершины x->par нет родителя, т.е. эта вершина – корневая. В таком случае мы просто перекрашиваем вершину x->par в черный цвет и процесс завершается.

Все случаи рассмотрены.

Итак, после добавления вершины процесс приведения дерева к виду красно-черного дерева сводится к некоторому количеству процедур перекраски 1 (не более h раз, где h – высота дерева) и не более чем к двум поворотам. Причем, после поворотов дерево не требует дальнейших изменений.

Итак, мы доказали следующую теорему

Теорема. Указанный алгоритм позволяет добавлять вершину к красно-черному дереву за время T=O(log₂N) операций, где N – количество вершин в дереве.

Дата добавления: 2015-10-30