Удаление вершины из B-дерева

Для удаления элемента, равного заданному, требуется, сначала, его найти. При осуществлении поиска мы параллельно будем обеспечивать условие, гарантирующее, чтобы в вершине, из которой будет удаляться элемент, было бы не менее

n элементов (по определению В-дерева достаточно, чтобы в вершине присутствовало не менее n-1 элемента).

Итак, в процессе поиска вершины, содержащей удаляемый элемент v, мы вводим понятие текущей вершины x. Текущая вершина перемещается от корня дерева по соответствующей ветви к вершине, содержащей удаляемый элемент.

Для каждого очередного значения текущей вершины возможен один из следующих вариантов

1) Вершина является листом.

Если, при этом, вершина - корень (все дерево состоит из одной вершины), то мы просто удаляем найденный элемент из этой вершины (если элемент найден). Если дерево состоит более, чем из одной вершины, то в результате выполнения следующих пунктов, данная вершина содержит не менее n элементов и найденный элемент можно исключить из данной вершины (если он нашелся, иначе - элемент отсутствует в дереве).

2) Вершина x - внутренняя. Элемент v в вершине x не найден.

Ищем потомка x->child[i] вершины x, с которого начинается поддерево,

содержащее элемент v (если он вообще есть в дереве). По условию мы должны гарантировать, чтобы в вершине x->child[i] содержалось бы не менее n элементов. Если это выполняется, то переходим к рассмотрению этой вершины:

x=x->child[i].

Иначе мы либо `перетаскиваем' один элемент из брата вершины x->child[i] в

вершину x->child[i], либо, если это невозможно, объединяем данную вершину с братом. Более подробно, есть два варианта:

а) У вершины x->child[i] есть брат, содержащий не менее n элементов.

Пусть, для определенности, это - правый брат, т.е. x->child[i+1]->n ³ n.

Тогда мы переносим элемент x->value[i] в конец массива элементов x->child[i]

(соответственно, увеличив на 1 значение x->child[i]->n) и

элемент x->child[i+1]->value[0] переносим на место x->value[i]

(соответственно, уменьшив на 1 значение c->child[i+1]->n):

x->child[i]->value[++x->child[i]->n]=x->value[i];

x->value[i]=x->child[i+1]->value[0];

for(i=1;i<x->child[i+1]->n;i++)

x->child[i+1]->valuie[i-1]=x->child[i+1]->valuie[i];

x->child[i+1]->n--;

Например, требуется в следующем дереве удалить вершину 11 в В-дереве степени 3:

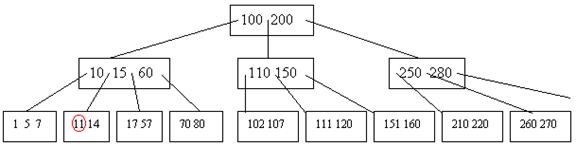
У данной вершины есть сосед (левый), содержащий 3 элемента. Тогда мы максимальный элемент из этой вершины – 7 – помещаем на место 10, а 10 помещаем на место 11:

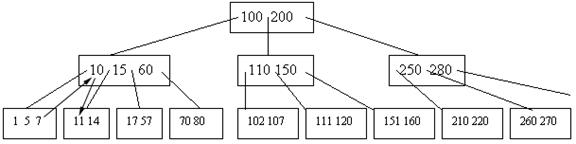
Теперь мы можем перейти к рассмотрению следующей вершины:

x=x->child[i];

б) У вершины x->child[i] все братья содержат n-1 элемент.

Допустим, для определенности, у вершины x->child[i] есть правый брат. Тогда, мы объединяем вершину x->child[i] с вершиной x->child[i+1] с помощью стыковочного элемента x->value[i]. Т.е. мы добавляем элемент x->value[i] в конец массива x->child[i]->value и затем добавляем все элементы из x->child[i+1] в конец массива x->child[i]->value.

Осталось удалить все лишнее: элемент x->value[i] из массива x->value, потомка x->child[i+1], ссылку x->child[i+1] из массива x->child.

Здесь мы воспользовались тем, что в вершине x есть хотя бы n элементов.

Например, требуется в следующем дереве удалить вершину 14 в В-дереве степени 3:

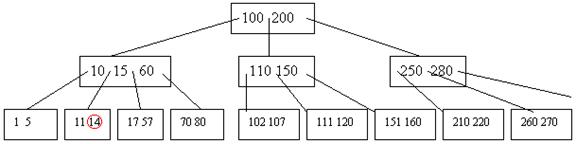
Для этого мы объединяем вершину {11,14} с элементом 15 и с вершиной {17,57}:

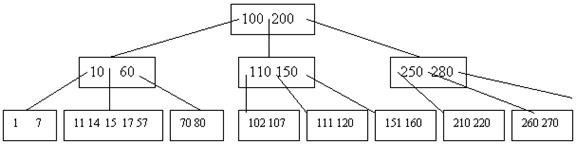
Теперь мы можем перейти к рассмотрению следующей вершины:

x=x->child[i];

3. Вершина x - внутренняя, в вершине найден элемент x->value[i]==v.

Сначала удаление производится аналогично дереву поиска: в одном из поддеревьев, соседних данной вершине, например, для определенности, в правом соседнем поддереве данной вершины (т.е. в поддереве, начинающемся с вершины x->child[i+1]) находим элемент v₀, ближайший к v. В нашем случае это – минимальный элемент поддерева, начинающегося с вершины x->child[i+1]. Далее, помещаем элемент v₀ на место элемента v и запускаем процедуру удаления старого (т.е. удаленного) элемента v₀.

Здесь, чтобы не запутаться в `старом’ v<sub>0</sub> и `новом’ v₀ лучше сначала запомнить адрес элемента, на который мы должны скопировать v₀ и само значение v₀, далее можно осуществить процедуру удаления элемента v₀ и только потом скопировать запомненное v₀ по запомненному адресу.

Лекция 12

Хеширование

Фактически, алгоритмы работы со всеми структурами данных, связанными с деревьями, основаны на операции сравнения. Можно использовать другой подход. Попробуем на основе значения элемента x, заносимого в структуру данных, вычислять некоторую функцию h(x), которая будет так или иначе отражать положение элемента x в структуре данных (например, индекс элемента в массиве). Такая функция называется хэш-функцией. Сама структура данных, поиск элементов в которой использует хэш-функцию, называется хэшируемой.

Наиболее прямолинейным способом хранения хэшируемых данных является массив массивов элементов. Т.е. для каждого значения хэш-функции отводится свой массив, в котором хранятся элементы, рассматриваемого типа. Например, для работы с множеством целых чисел, при использовании хэш-функции h(x) со значениями 0£h(x)<M, можно использовать массивы

int h_array[M][N], l_array[M];

Здесь константа N задает ограничение на количество чисел, содержащихся в структуре данных, для каждого значения хэш-функции. Данные, соответствующие значению хэш-функции h(x)=i, хранятся в массиве h_array[i], количество элементов в этом массиве хранится в переменной l_array[i].

Преимущества и недостатки такого подхода очевидны: основным преимуществом является простота и удобство работы при равномерном распределении значений хэш-функции, а недостатком – неэффективность при неравномерной работе хэш-функции. Отметим также, что время работы для добавления элемента меньше времени работы для удаления элемента, т.к. в последнем случае приходится сдвигать часть массива.

---

Дата добавления: 2015-10-30