Характеристика форм розподілу

Найпростішою мірою асиметрії є відхилення між 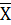, Ме, Мо.

У симетричному (нормальному) розподілі: 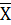=Мe= Мo, а R=6σ; σ=1,25 .

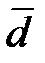При правосторонній асиметрії 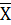>Ме> Мо.

При лівосторонній 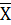<Ме< Мо.

Тобто у симетричному ряді розподілі рівновіддалені від центру значення ознаки мають однакові частоти.

Для характеристики 2-х або декількох рядів використовується коефіцієнт асиметрії (А):

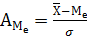або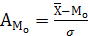

Якщо А>0 – правостороння асиметрія;

А<0 – лівостороння;

А=0 – симетричний розподіл.

Чим ближчий чисельник коефіцієнта (А) до нуля, тим менша асиметрія.

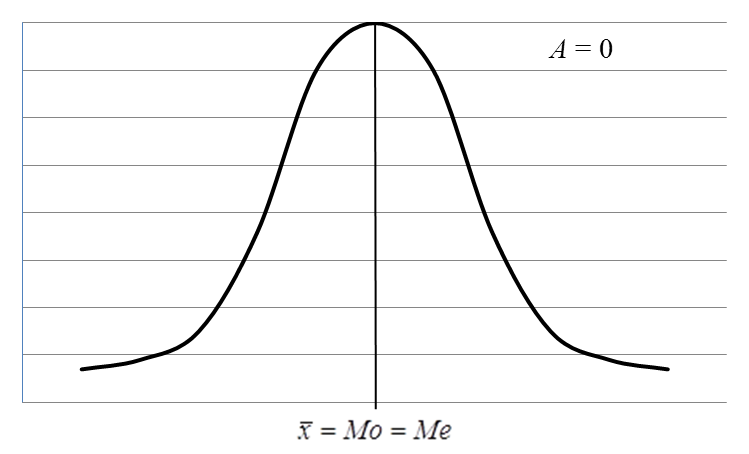
Рис. 1 – Симетричний розподіл

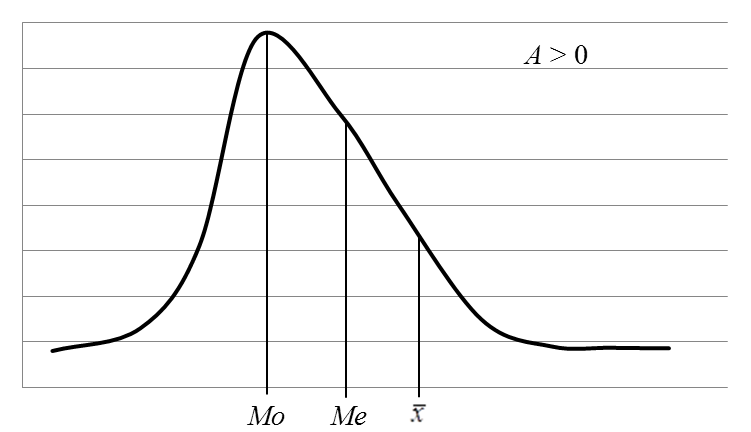
Рис. 2 – Правостороння асиметрія

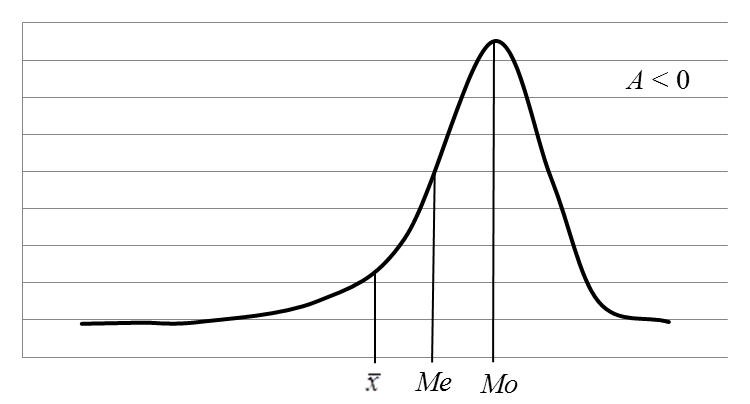
Рис. 3 – Лівостороння асиметрія

Криві розподілу мають різну гостровершинність. Крутизна, гостровершинність або пологовершинність кривої розподілу називають ексцесом.

Розрізняють ексцеси: нормальний, вище нормального, нижче нормального.

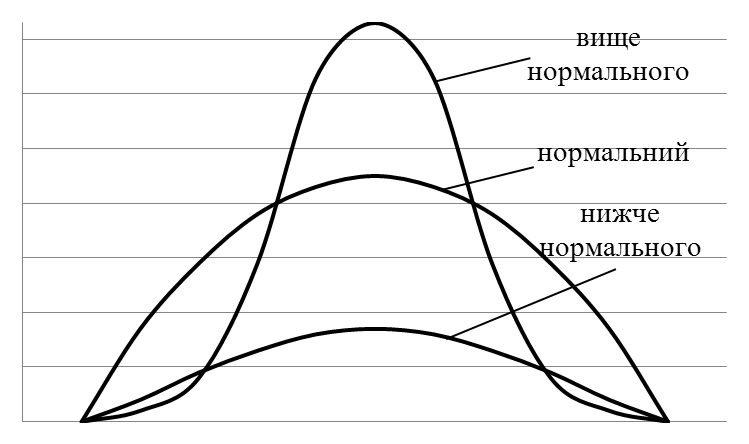
Рис. 4 – Види розподілів, залежно від ексцесу

Для характеристики ексцесу застосовується коефіцієнт ексцесу, який розраховується на базі центральних моментів розподілу (ЦМР).

ЦМР – це середнє арифметичне k –го ступеня відхилення варіантів ознаки від їх середньої величини.

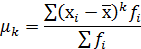
Тоді при k=0 отримаємо ЦМР нульового порядку.

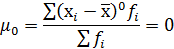
При k=1 отримаємо ЦМР І-го порядку = 0.

При k=2 – ЦМР ІІ-го порядку = дисперсії.

k=3, ЦМР – характеризує асиметрію і використовується при розрахунку стандартизованого коефіцієнту асиметрії (відношення ЦМР ІІІ-го порядку до СКВ у кубі).

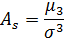
При правосторонній асиметрії ,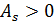

лівосторонній асиметрії ,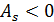

в симетричному розподілі .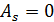

Цей показник асиметрії більш точний, ніж попередні і застосовується більш широко.

Вважається, що при 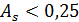асиметрія незначна.

При 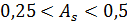– середня.

При 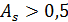– значна.

ЦМР IV-го порядку використовується для характеристики ексцеса (при розрахунку коефіцієнта ексцеса):

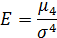
Якщо розподіл нормальний (симетричний), то ексцес – нормальний Е=3.

При: Е>3 – вище нормального (гостровершинний);

Е<3 – нижче нормального (плосковершинний).

Розглянуті характеристики варіаційних рядів допомагають більш детально вивчити особливості статистичних сукупностей та їх закономірності.

Висновок: При вивченні даної теми потрібно звернути особливу увагу на той факт, що в аналітичній роботі не можна обмежуватися обчислювачем і аналізом середніх величин. Якісний аналіз не можливий без вживання показників варіації, які дають не менше цінну інформацію про вивчення явища, ніж середні величини.

Дата добавления: 2015-10-30