Operators. Expressions use familiar arithmetic operators and precedence rules.

+	Addition
-	Subtraction
*,.*	Multiplication, element-by-element multiplication
/,./	Right division, element-by-element right division
\,.\	Left division (described in Linear Algebra in the SCILAB), element-by-element left division
^,.^	Power(exponent), element-by-element power
()	Specify evaluation order
~	Logical NOT
|	Logical OR
&	Logical AND
==, >=, <=, <, >, <>, ~=	Equal to, equal or greater than, equal or less than, greater than, less than, not equal to (two alternatives)

Add and Subtract

Scilab knows how to add and subtract numbers, arrays, and matrices. As long as A and B are two variables of the same size (e.g., both 2x3 matrices), then A + B and A − B will add and subtract them as matrices:

A=[1,2,3;4,5,6;7,8,9]

B=[3,2,1;6,4,5;8,7,9]

A+B

A-B

Multiplication

The usual multiplication sign * has special meaning in Scilab. Because everything in Scilab is a matrix, * means matrix multiply. So if A is a 3x3 matrix and B is another 3x3 matrix, then A*B will be their 3x3 product. Similarly, if A is a 3x3 matrix and C is a 3x1 matrix (column vector) then A ∗C will be a new 3x1 column vector. And if you want to raise A to a power by multiplying it by itself n times, you just use A^n.

For a language that thinks everything in the world is a matrix, this is perfectly natural. Try

A*B

A*[1;2;3]

A^3

But there are lots of times when we don’t want to do matrix multiplication. Sometimes we want to take two big arrays of numbers and multiply their corresponding elements together, producing another big array of numbers. Because we do this so often Scilab has a special symbol for this kind of multiplication:.*

For instance, the dot multiplication between the arrays [a,b,c] and [d,e,f] would be the array [a*d,b*e,c*f]. And since we might also want to divide two big arrays this way, or raise each element to a power, Scilab also allows the operations./ and.^ For example, try

[1,2,3].*[3,2,1]

[1,2,3]./[3,2,1]

[1,2,3].^2

Multiplication by the Dot Operator (.*) is necessary to tell Scilab it should multiply the vectors element--by--element. Change to ordinary multiplication (*) and you’ll get error message on the Console.

These “dot” operators are very useful in plotting functions and other kinds of signal processing.

Division

Scilab allows left and right element-by-element division.\ and./ respectively. The difference between the two is which of the two division elements is the numerator and which the denominator. Left division means that the element in the left matrix becomes the denominator, with right division it is the nominator.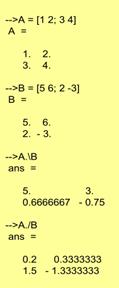

Practical problems often require the determinant of a (square) matrix to be calculated. The command det() returns the determinant.

Backslash (\) denotes left matrix division. x=A\b is a solution A*x=b, which is important e.g. in control engineering. If A is square and nonsingular x=A\b is equivalent to x=inv(A)*b, but the computation burden is smaller and the result is more accurate.

A requirement of nonsingular square matrices is that the determinant is nonzero. Consider the following cases:

, it is therefore nonsingular,

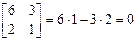meaning that it is singular

Before performing left division with square matrices one should check that the determinant of the coefficient matrix, e.g. by testing that clean(det(A)) ~= 0.

Дата добавления: 2015-10-29