Норма бағдарламалау жүйесі.

НОРМАтілі мамандандырылған процедуралық емес тіл болып табылады. Ол негізінен есептеуіш сипатындағы мәселелерді шешуге, дербес жағдайда математикалық физика есептерін шешуге арналған десе болады. Тілдің барлық конструкциялары декларативті сипатта және мәндерді есептеу ережесін суреттейді. Тілдің негізгі тағайындалуы бағдарламаны құрастыру процесін автоматтандыру болып табылады. Бағдарламашы мұнда негізінен математикалық формулалар терминінде жұмыс істегендіктен, ол өз кезегінде оның жұмысын айтарлықтай жеңілдетеді және ықшамдайды. Транслятордың жұмысы күрделенеді. Дәстүрлі мәселелермен қатар, мысалы, дербес жағдайда синтаксистік және семантикалық талдау, ол шығыс бағдарламасының синтезін орындайды.

Берілген есептің спецификациясына сәйкес бағдарламаны автоматты түрде құруға мүмкіндік беретін идеялар, 1963 жылы И. Б. Задыхайлоның жұмысында [21] келтірілген. Ол идеялардың одан ары дамуы НОРМА тілінің және әртүрлі платформалар үшін транслятордың бірнеше нұсқауының пайда болуына әкелді.

Алғашында НОРМА термині (Непроцедурное Описание Разностных Моделей Алгоритмов) алгоритмдердің айырымдық модельдерінің процедуралық емес сипаттамасы деп таратылып айтылды. Соңынан басқа трактовка пайда болды: – (НОРМАльный уровень общения прикладного математика с компьютером) қолданбалы математиктің компьютермен қатысының НОРМАльды деңгейі. Қолданбалы бағдарламаны құрастырушы, нақты компьютердің ерекшеліктерін негізге ала отырып, өз пәндік облысының үйреншікті терминінде ойлайды. РҒА (РАН) В. М. Келдыш атындағы қолданбалы математика институтының нақты қажеттіліктерін ескере отырып, тілдің авторлары математикалық физика мәселелерін шешуді барынша (максималды) ықшамдауға тырысты. Пәндік облыс спецификасы - бұл торлық тәсілдерді негізге алу, соларға бағытталу.

НОРМА тіліндегі бағдарлама жазбасы операцияның орындалу реті туралы ешқандай мәліметті қажет етпейді. Тіл сөйлемдерінің реті еркін болуы мүмкін. Есептеулерді қалай ұйымдастыру керек екенін түсіндірмей ақ, бұл тілде есептеулерге сұраныс жасау мүмкіндіктері қарастырылған. Барлық ақпараттық байланыстар, берілген бағдарламаны талдау және шығатын тексті синтездеу этапында транслятор–синтезатормен анықталады және ескеріледі.

Есептеулерді ұйымдастырудың нақты тәсілін таңдау трансляторға жүктеледі. Дербес жағдайда, мысалы, қорытынды бағдарламаны синтездеу этапында, ол тізбекті кодты да, параллель кодты да генерациялай алады.

НОРМА тілінің жоғары деңгейін таңдау оның өзіне тән сипатын анықтайды – бұл айнымалыны бір реттік меншіктеу тілі. Мұнда әрбір айнымалы өзіне бір рет қана мән қабылдай алады және жады, қосымша әсер, меншіктеу операторы және басқарушы операторлар сияқты түсініктер НОРМА тілінде «анықтама бойынша» жоқ. Барлық дәстүрлі бағдарламалау тілдерінде бұл түсініктер бар, себебі олардың көмегімен үнемділік, жадының таратылуы, операторлардың орындалу ретін анықтау және т.б. сұрақтарды ескере отырып нақты алгоритм құру керек болады. Негізінде НОРМА тіліндегі жазба, берілген нақты есепті шешудің сандық әдісінің жазбасы болып табылады.

НОРМА тіліндегі жазбаларда артық ақпараттық байланыстар болмайтындығы да маңызды. Мұндай байланыстар әдетте бағдарламалау процесі барысында пайда болады, және олар алгоритмдер мен бағдарламаны ықшамдау кезінде анық көрінеді. Бағдарламалардың дәл ақпараттық құрылымын анықтау күрделі мәселе болып табылатыны белгілі. НОРМА тілі бізге бағдарламаның тізбекті этапын өткізуге мүмкіндік береді, ал параллель бағдарламаны генерациялау үшін бірден математикалық формулалар терминіндегі жазбасынан бастауды ұсынады. Бұл пайымдау бойынша, dataflow-компьютерлерін бағдарламалау үшін НОРМА тілінің потенциалын зерттеу өте қызықты болары анық.

Алынған нәтижелер авторлармен шынайы транслятор-синтезатор құру барысында пайдаланылды. НОРМА тілінің сипаттауы бойынша, ол тізбекті компьютерлер үшін де, таратылған жадылы және ортақ жадылы параллель есептеу жүйелері үшін де шығыс бағдарламаларын алуға мүмкіндік береді. Бұл бағдарламалар Fortran MPI, Fortran PVM, Fortran 77 және Fortran тілінің басқа да диалектілерінде жазылуы мүмкін.

Төменде НОРМА тілінің қысқаша сипаттамасы жұмыс стандарты [1] және http:// www.keldysh.ru/norma сайтының деректері бойынша беріледі.

НОРМА тіліндегі бағдарлама бір немесе бірнеше бөлімдерден тұрады. Бөлімдер үш түрлі болуы мүмкін – негізгі (басты) бөлім, қарапайым бөлім және функция-бөлім. Бөлімнің түрі сәйкесінше MAIN PART, PART және FUNCTION кілттік сөздерімен анықталады. Бөлімдер бір-бірін өз атауларымен шақырулары және деректерді формальды және фактілік параметрлер механизмі, болмаса сыртқа файлдар арқылы INPUT және OUTPUT сипаттамалары көмегімен жіберуі мүмкін. Бөлімдерді рекурсивті шақыруларға тыйым салынған.

НОРМА тілінде ауқымды айнымалылар түсінігі жоқ.

Бағдарламада, RESULT кілттік сөзіне дейінгі формальды параметрлер тізімінде көрсетілген барлық параметрлер бастапқы деректер, ал ол кілттік сөзден кейінгі келтірілген параметрлер есептеу нәтижелері болып есептеледі. Бір параметр бір мезгілде бастапқы және нәтиже бола алмайды, себебі бұл айнымалылардың мәндерді қайта меншіктеуіне алып келеді, ал НОРМА тілінде қайта меншіктеуге рұқсат етілмейді. Функция-бөлімінде RESULT кілттік сөзі қолданылмайды, себебі функцияны есептеу нәтижесі функцияның атауымен және типімен байланыстырылады.

Бөлім денесінде сипаттаулар, операторлар және итерациялар берілулері мүмкін. Олардың орналасу тәртібі, жалпы айтқанда еркін – мүмкін болатын шектеулер транслятордың кіріс тілін сипаттау кезінде анықталады.

НОРМА тілінің базалық ұғымы облыс болып табылады. Облыс - бұл n -өлшемді индексті кеңістікте нүктелер координатасын беретін

{ i₁, …, i_n }, n > 0, i_j > 0, j =1… n,

түріндегі бүтінсанды жиынтықтар бірігуі. Есептің n -өлшемді кеңістігінің әрбір координат өсімен индекс аты байланыстырылады.

Бірөлшемді облыс үғымы, облыстарды сипаттау кезіндегі басты маңызды ұғым болып табылады. Бірөлшемді облыс, индекстік кеңістіктегі қандай да бір координат өсінде нүктелер диапазонын беру үшін қызмет етеді. Дербес қарапайым жағдайда бірөлшемді облысты сипаттау кезінде, бірөлшемді облыстың аты, индекс аты және индекс мәндерінің өзгеру шекаралары көрсетіледі. Мысалы, НОРМА тілінің келесі екі сипаттаулары:

ks: (k = 1..n).

js: (j = 1..10).

бірөлшемді екі облысты енгізеді. Бірінші жағдайда, үстінгі шекара n параметрінің көмегімен берілген (барлық параметрлердің мәндері параметрлерді сипаттау бөлімінде сипатталуы керек). Екінші жағдайда өлшем айқын көрсетілген. Диапазон шекаралары болып, бүтін тұрақтылардан, облыс параметрлерінен және арифметикалық операциялардан тұрғызылған бүтін оң тұрақты өрнектер алынады.

Көпөлшемді облыс «;» таңбасымен белгіленетін облыстарды көбейту операциялары көмегімен тұрғызылады. Төменде бірөлшемді облыстарды Dirk және Dirl көбейту операциясы көмегімен алынған екіөлшемді облысты сипаттау мысалы көрсетілген:

Square: (DirK: (k=1..15); DirL: (l=1..5))

Енгізілген тікбұрышты square облыс екіөлшемді индексті кеңістіктің ішкі жиыны болып табылады. Оған бірінші координатасы 1 ден 15-ке дейін, ал екіншісі 1 ден 5-ке дейінгі мәндер болатын нүктелер кіреді.

Тікбұрышты А және В облыстарын көбейту «;» операциясы коммутативті қасиетке ие, яғни А; В=В; А. Бұл, дербес жағдайда, облысты сипаттау кезінде, индексті кеңістік бағыттарының реті бекітілмейтінін білдіреді. Егер индексті кеңістік бағыттарын бекіту қажет болса, онда INDEX кілттік сөзі көмегімен облыс индекстерінің сипаттауы беріледі.

Барлық облыстарды айқын түрде сипаттау міндетті емес, мұнда енгізіліп қойылған атауларды да пайдалануға болады. Мысалы,

NewGrid: (ks;js).

жоғарыда анықталған ks және js бірөлшемді облыстары арқылы облысты анықтайды. Енгізілген облыстарды өзгертуге болады. Облыстарды модификациялау (өзгерту) бірнеше нүктелер санын қосу, нүктелерді жою немесе диапазонын өзгерту арқылы орындалуы мүмкін. Екі алғашқы типтерді модификациялау LEFT(n) және RIGHT(n) шекара функциялары көмегімен сипатталады. LEFT(n) функциясы диапазонның сол жақ шекарасына, ал RIGHT(n) функциясы – диапазонның оң жақ шекарасына қолданылады. Функция алдына қойылған «+» таңбасы бірөлшемді облысқа нүктелер қосылатынын, ал «-» таңбасы бірөлшемді облыстан нүктелер жойылатынын білдіреді. Бұл екі функцияда, облыстан жоюға немесе облысқа қосуға қажетті нүктелер санын анықтайтын бір ғана параметр n болады. LEFT және RIGHT функцияларының нақты параметрлері ретінде тек бүтін оң тұрақты берілуі мүмкін. Функцияларға қатынас, модификация жасалатын диапазонды беретін бір өлшемді облыс атымен тек контексте ғана мүмкін болады. Бағдарламада келесі сипаттау бар делік:

DirK:(k=1..15)

Онда k=3..18 нүктелерінен тұратын DirKm облысын келесі түрде беруге болады:

DirKm: DirK-LEFT(2)+RIGHT(3)

Диапазонды айқын түрде қайта анықтай отырып, құрамдас бірөлшемді облысты өзгертуге болады. Ол үшін модификацияда индекс аты мен оның жаңа мәнін көрсету керек. Бағдарламада келесі сипаттау бар делік:

Square: (DirK:(k=1..15); Dirl: (l=1..9))

Жасалған сипаттауды модификациялау үшін және бір индекс бұрынғыша 1-ден 15-ке дейін өзгеретін, ал басқасы 10-нан 22-ге дейін өзгеретін облысты анықтау үшін, келесі конструкцияны пайдалануға болады:

SquareNew: Square/l=10..22

Облыс индекстерін байланыстыратын қарапайым қатынастар көмегімен облысты модификациялау мүмкіндігі бар. Мысалы,

KL: ((k=1..10);(l=1..10)). Diagonal: KL/k=1

сипаттауы (k=1,l=1), (k=2,l=2), …,(k=10,l=10) нүктелерінен тұратын Diagonal облысын береді.

Айта кету керек, облыс тек қана индексті кеңістік нүктелері координаттарының мәндерін ғана анықтайды (осы нүктелердегі есептеу шамаларының мәндері емес). Егер Y_ij, i, j= 1 …n шамасының мәндерін, есепті шешу барысында X_ij=F(i, j) формуласымен енгізілген X_ij, i, j=1…n торында есептеу талап етілсе, онда келесі қадамдар тізбегін орындау керек:

1. i, j=1…n нүктелерінен тұратын облысты сипаттау.

2. Осы облыста Х және У шамаларын сипаттау.

3. Осы облыста X_ij=F(i, j) торының және Y_ij=G(X_ij) мәндерін есептеу ережесін беру.

НОРМА тілінде облыстарды айқын сипаттаумен қатар, шартты облыстарды беру мүмкіндігі де қарастырылған. Индекстік кеңістік нүктелерінің шартты облысқа кіруі немесе кірмеуі, қандай да бір шарттың орындалуы немесе орындалмауына байланысты анықталады. Шартты облысты беру идеясы қарапайым. Ертерек анықталған D облысы екі қиылыспайтын D₁ және D₂ ішкі облыстарға бөлінеді. Бірінші ішкі облыс берілген шарт ИСТИНА мәнін қабылдайтын D облысының нүктелерінен, ал екінші ішкі облыс берілген шарт ЛОЖЬ мәнін қабылдайтын нүктелерден тұрады. Square облысының алдыңғы сипаттамасын алып, соның негізінде шартты облыстарды берейік:

Square1, Square2: Square/x[k,1]-y[k,1]<eps

Берілген сипаттама бастапқы облысты Square екі қиылыспайтын Square1 және Square2 ішкі облыстарға бөлуді береді, және Square1∩Square2=Ø, ал Square1USquare2=Square. Бірінші Square1 ішкі облысы, x[k,1]-y[k,1]<eps шарты ИСТИНА мәнін қабылдайтын Square облысының нүктелерінен тұрады, ал Square2 ішкі облысы, ЛОЖЬ мәнін қабылдайтын нүктелерден тұрады.

НОРМА тілінде шамалардың екі класы анықталған: скаляр шамалар және облыстағы шамалар. Сипаттама ағымды бөлімде әрбір шамаға сәйкес бірегей ат қояды, сонымен қатар шаманың типін береді: REAL, INTEGER немесе DOUBLE. Скаляр шаманы сипаттау, мысалы, келесі түрде болуы мүмкін:

VARIABLE k1,k2 INTEGER

VARIABLE pi DOUBLE

Әрбір облыстағы шамалар сипаттамада көрсетілген облыспен байланыстырылады. Бұл облыс, берілген шамаға қатынас кезінде индексті өрнектерде пайдаланылуы мүмкін индекс аттарын анықтайды. Индексті өрнектерді көрсету реті маңызды емес. Облысты сипаттау кезінде енгізілетіндіктен, индекстер үшін арнайы сипаттау талап етілмейді.

Тағы да Square облысының алдыңғы берілген сипаттамасын пайдаланайық және соның негізінде облыстағы шамаларды енгізейік:

Square: (DirK:(k=1..15); Dirl: (l=1..9))

VARIABLE Xsum, Y DEFINED ON Square

OneDimK DEFINED ON DirK, OneDimL DEFINED ON DirL

Келтірілген сипаттаулар Square облысында Xsum және Y шамаларын анықтайды. Индексті өрнектерде бұл екі шама да k және l индекстеріне ие болуы мүмкін. OneDimK және OneDimL шамалары DirK және DirL облыстарында анықталған, сондықтан олар индексті өрнектерде сәйкесінше k және l индекстеріне ие болулары мүмкін.

Облысты сипаттау кезінде индексті кеңістік бағыттарының реті бекітілмегендіктен, Y[k-1,l+1] және Y[l+1,k-1] қатынастары эквивалентті. Егер бір индексті бағытты басқасымен байданыстыру қажет болса, онда оны айқын түрде көрсету керек. Мысалы, Y матрицасының диагоналдық элементтерін Y[k,l=k] немес жай Y[l=k] деп анықтауға болады.

НОРМА тілінде операторлардың үш түрі ғана анықталған: скалярлық оператор, ASSUME операторы және бөлімді шақыру.

Скалярлық оператор скалярлардың арифметикалық мәндерін есептеуге арналған. Жалпы алғанда бұл оператор дәстүрлі бағдарламалау тілдеріндегі қабылдау операторының аналогы десе болады, сол жағында скаляр аты көрсетіледі, ал оң жағында – скалярлық арифметикалық өрнек. Мысалы:

d = 1997

c = b+e+SQRT(d+4)

Скалярлық операторда қайта меншіктеу рұқсат етілмейді, сондықтан k=k-1 түріндегі оператор анықтама бойынша дұрыс емес дептесептеледі.

ASSUME операторы облыста анықталған шамалардың арифметикалық мәндерін есептеу үшін пайдаланылады. Бұл оператордың семантикасы келесі түрде анықталады. Шартты түрде жазылған қатынасты қарастырайық:

FOR D(i₁,…,i_n) ASSUME

мұндағы:

· D(i₁,…,i_n) – ASSUME операторының облысы;

· (i₁,…,i_n) – D облысының индекстері;

· - облыста анықталған шамалардың аттары;

· - сол жақтағы индекстік өрнектер;

· - оң жақтағы индекстік өрнектер;

· F – оң жақтағы есептелетін функция;

· Other – оң жақтың басқа термалары.

Әрбір осындай қатынас, оң жақтағы шамаларының мәндері және Other термалары бойынша, сол жақтағы X ^l шамасының мәнін есептеу F ережесін береді. Ол келесі түрде жүргізіледі:

· Барлық нүктелері анықталады;

· Әрбір нүктесі үшін нүктесінде сол жақтағы X ^l шамасының мәнін есептеу талап етіледі;

· Әрбір нүктесі үшін барлық шамаларының индекстің өрнектерінің 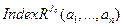мәндері есептеледі:

· Егер қандай да бір уақыт мезетінде нүктесі үшін Х барлық аргументтері есептеліп қойылса, онда сол жақтағы шамасының мәндерін есептеу мүмкін болады; ал егер аргументтер толық анықталмаса, онда дәл осы мезетте берілген нүктені есептеу мүмкін емес (бірақ ол тіпті мүмкін емес дегенді білдірмейді).

Берілген оператор шаманың мәндерін есептеу ережесін анықтайды. Сонымен қатар ол бағдарламаның берілген орнында есептеудің тез арада орындалуын талап етпейді және есептеу тәсілін немесе ретін белгілемейді. Оператор тізбекті болмаса параллель орындалу жайында ешқандай ақпаратты қамтымайды. Өзімізге таныс сипаттауларды қарастырайық:

Square: (DirK: (k=1..15); DirL: (l=1..9))

VARIABLE Xsum, Y DEFINED ON Square,

Төменде келтірілген оператор

FOR Square ASSUME Xsum = 0

Xsum шамасының 135 элементін нөлдік етуді береді. НОРМА тілінде бұл сұраныстың іске асырылуы бекітілмейді.

Жалпы алғанда бұл параграфта НОРМА тілінің негізгі идеясын сипаттап өттік десек болады. Есептеу барысында қажет етілетін басқа да сұрақтар туралы толық мағлұматты [1] әдебиеттен табуға болады.

Параграфтың соңында НОРМА тілінде жазылған сызықты теңдеулер жүйесін Гаусс-Жордан әдісімен шешудің бағдарламасын қарастырайық. Аталған әдістің есептеу формулаларын келесі түрде жазуға болады:

Бағдарлама тексті төменде келтірілген. Ондағы жолдардың нөмірленуі тілдің міндетті элементі болып табылмайды, ол тек операторлардың мағынасын кезекті түсіндіру үшін ғана пайдаланылған.

1 MAIN PART Gauss.

2 BEGIN

3 INDEX k,l.

4 ks: (k=1..n).

5 ls: (l=1..n).

6 kls: (ks; ls).

7 VARIABLE a DEFINED ON kls.

8 VARIABLE b, x DEFINED ON ks.

9 INPUT a (FILE=’gauss’) ON kls,

10 b(FILE=’gauss’) ON ks.

11 DOMAIN PARAMETERS n=4.

12 COMPUTE Calculate(a ON kls, b ON ks RESULT x ON ks).

13 OUTPUT x(FILE=’gauss.out’,TAB(10),’Решение:’,STR(1)) ON ks.

14 END PART.

15 PART Calculate.

16 a,b RESULT x

! Раздел вычислений

17 BEGIN

18 INDEX I,j

19 so:(ijs: is: (i=1..n); js: (j=1..n));ts: (t=0..n)).

20 slo: ts;is). s:so/ts-LEFT(1). Sl:slo/t=1..n.

21 VARIABLE a DEFINED ON ijs.

22 VARIABLE b, x DEFINED ON is.

23 VARIABLE m DEFINED ON so.

24 VARIABLE r DEFINED ON slo.

25 DOMAIN PARAMETERS n=4.

26 DISTRIBUTION INDEX i=2..8, j=1.

27 FOR so/t=0 ASSUME m=a.

28 FOR slo/t=0 ASSUME r=b.

29 sa,sb:s/i=t. sal,sbl:sl/i=t.

30 MACRO INDEX ti [t-1,i=t].

31 MACRO INDEX tij [ti,j=t].

32 FOR sa ASSUME m=m[ti]/m[tij].

33 FOR sal ASSUME r=r[ti]/m[tij].

34 FOR sb ASSUME m=m[t-1]-m[t-1,j=t] * m[i=t].

35 FOR sbl ASSUME r=r[t-1]-m[t-1,j=t] * r[i=t].

36 FOR is ASSUME x = r[t=n].

37 END PART

Бағдарлама операторларына түсініктеме берейік. Төменде пайдаланылған нөмірлер бағдарлама жолдарының нөмірлеріне сәйкес келеді.

(1) Gauss бағдарламасының басты бөлімінің тақырыбы.

(2) Басты бөлімнің басталуы.

(3) Облыстардың индекстерін сипаттау.

(4-6) Есептің бастапқы деректері анықталған is, js бірөлшемді облыстары және ijs көпөлшемді облысын анықтау.

(7-8) a, b, және x айнымалыларын сипаттау, мұндағы a – жүйе коэффициенттерінің матрицасы, b – бос мүшелер бағаны, x - жүйені шешу нәтижесі.

(9-10) gauss.dat файлынан бастапқы деректерді енгізу.

(11) Облыстар параметрін беру.

(12) Есептеу жүргізетін Calculate бөлімін шақыру.

(13) gauss.out файлына нәтижені шығару.

(14) Басты бөлімнің соңы.

(15) Calculate бөлімінің тақырыбы.

(16) Бөлімнің (a, b) кіріс және (х) шығыс параметрлерін белгілеу.

(17) Жәй бөлімнің басталуы.

(18) Облыстардың индекстерін сипаттау.

(19) ts және ijs облыстарынан тұратын көпөлшемді so облысын анықтау. Өз кезегінде ijs облысы is және js облыстарынан тұрады.

(20) Облысты модификациялау операциялары көмегімен s, s1 облыстары және slo шартсыз облысы анықталады.

(21-22) Бөлім параметрлері болып табылатын айнымалыларды сипаттау.

(23-24) m және r айнымалыларын сипаттау.

(25) Облыстар өлшемдерін беру.

(26) Таратылу индекстерін сипаттау.

(27-28) m және r айнымалыларының бастапқы мәндерін беру.

(29) Қосымша шартты sa,sb,sal,sbl облыстарын сипаттау.

(30-31) Индекстік конструкцияларды сипаттау. Индекстік конструкциялар күрделі индекстік өрнектердің жазылуын қысқарту үшін қолданылады.

(32-36) Сәйкес есептеу формулалары үшін есептеулер.

(37) Бөлімнің соңы.

Дата добавления: 2015-10-29