Бекітілім 1.2.3

Берілген функция n айнымалыға тәуелді болсын және аргументтер саны р-дан аспайтын операциялардың шектеулі санының суперпозициясы ретінде берілсін. Оның мәндері осы операцияларды пайдаланатын қандай да бір алгоритмнің көмегімен есептелінеді делік. Егер деректердің енгізілуі ескерілмесе және алгоритмнің биіктігі s – ке тең болса, онда s ≥ log_pn.

Енді алгоритм графының канондық параллельдік формасын қарастырайық. Нөлдік яруста, кіріс айнымалыларының енгізу мәндеріне сәйкес келетін шыңдар (төбелер) орналассын. Соңғы s -ші яруста бір ғана шың орналасады. Сонымен әрбір шыңдағы кіретін доғалар саны р -дан аспайтындықтан, (s – 1)-ші ярустағы шыңдар саны р -дан аспайды, (s – 2)-ші ярустағы шыңдар саны р² -ден аспайды және тағы с.с. Нөлінші ярустағы шыңдар саны р^s –тен аспайды. р^s ≥ n болатыны түсінікті, сондықтан s ≥ log_pn.

Сонымен, егер қандай да бір есеп n кіріс деректерімен анықталса, онда жалпы жағдайда біз биіктігі log n аспайтын оның шешімінің алгоритмі бар болатынына сенім артпауымыз керек. Егер алынған алгоритм биіктігінің реті log^α n, α > 0 болса, онда бұндай алгоритмді біз параллельдік есептеу жүйесінде іске асырылу уақытысы жағынан тиімді деп санауымызға болады. Егер, әрине оның іске асырылуының барлық басқа да аспектілерін есепке алмасақ.

Вектор у,квадраттық матрица А және реті n болатын х векторының көбейтіндісі ретінде есептеледі делік. Егер у_i, a_ij, x_j сәйкес векторлар және матрицаның элеметтері болса, онда кез-келген i үшін

Айталық, берілген есептеу жүйесінде n² процессор бар болсын. Онда бірінші қадамда a_ij x_j – дің барлық n² көбейтіндісін параллель есептеуге, ал одан соң, қосуға арналған екіеселену схемасын пайдаланып, [log₂ n ] қадамда у векторының координаталарын анықтайтын барлық n қосындыны параллель есептеуге болады. Олай болса, квадраттық матрица және реті n болатын вектордың көбейтіндісін есептейтін алгоритм (биіктігінің реті log₂ n) тұрғыза аламыз. Сонымен қатар, алгоритмнің ені n² тең. Процессорлар біркелкі қолданылмайды. Тек бірінші қадамда ғана барлық процессорлар іске араласады. Одан кейін, жұмыс істейтін процессорлардың саны әрбір қадам сайын екі есе азаяды. 1.2.3бекітіліміне сәйкес, биіктігі кіші болатын алгоритмді тұрғызуға болмайды. Бірақ, логарифмдік биіктікте ені кішірек болатын алгоритмдер кездеседі.

Реті n болатын екі матрицаны көбейту есебін, бір матрицаның және реті n болатын n тәуелсіз векторлардың n көбейтіндісін есептеу есебі деп қарастыруға болады. Мұндағы векторлар ретінде екінші матрицаның бағандары алынады. Егер барлық осы көбейтулерді мазмұндалған алгоритм бойынша параллель есептейтін болса, онда алынған алгоритмнің биіктігі log₂ n және ені n³ тең болады. Тағы да процессорлар біркелкі пайдаланылмайды және тағы да биіктіктігі кіші болатын алгоритмді құрастыруға болмайды, бірақ мұнда да логарифмдік биіктікте ені кішірек болатын алгоритмдер кездеседі.

Ал енді келесі жағдайларға назар аударайық. Егер келтірілген алгоритмдерді канондық параллель форма ярустары арқылы іске асыруға талпынып көрсек, онда бірдей мәліметтерді көптеген процессорларға бір уақытта жіберу қажеттілігі туындайды. Бұндай операцияны өте жылдам орындауға болмайды. Сондықтан да нақты жағдайларда мәліметтерді жіберуге кеткен уақыт есептеу процесін айтарлықтай тежейді.

Биіктігі ең кіші болатын параллель алгоритмдерді құрастыру, матрица-векторлық қосу және көбейтуде ешқандай қиындық тудырған жоқ десе болады. Демек, бұндай алгоритмдерді басқа да матрица-векторлық есептер үшін оңай құрастыруға болады деген ой тууы мүмкін. Бұндай ой әрине дұрыс емес. Қарастырылған алгоритмдер дербес идеалды жағдайларда ғана іске асуы мүмкін.

Берілген x₀, x_-1,, x_-r+1 векторларын пайдалана отырып, келесі түрдегі сызықтық рекурренттік қатынастар:

(2.1)

көмегімен х_i 1 ≤ i ≤ s векторларын есептеу процесін қарастырайық [31]. Мұндағы А_ij, b_i – реті n болатынберілген матрица және вектор, олар n = 1 болғанда санға айналады. Біз мүмкіндігінше бекітілген (фиксированный) s кезіндегі биіктігі неғұрлым ең кіші болатын х₁, х_s векторларын есептеудің параллель алгоритмін тұрғызуымыз керек болды делік. Бұл жағдайда n²r процессорларды қолдана отырып, (2.1) қатынасының оң жағын шамамен log₂ nr қадамда есептеп шығуға болады. Бұл биіктігінің реті шамамен s log₂ nr болатын параллель алгоритмді береді. Бірақ-та биіктігі s -ке айтарлықтай әлсіз тәуелді болатын алгоритмді қалай тұрғызу керек екені және ондай алгоритмдердің бар болуы мүмкін екені туралы айқындылық жоқ.

Рекурренттік қатынасты (2.1) - матрица және реті үлкен векторлар арқылы біршама басқаша жазуға болады:

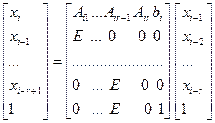
Матрицаны Q_i, ал сол жағындағы векторды у_i арқылы белгілейік. Онда

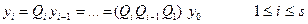
Матрица мен векторлардың реті nr + 1. Екіеселену алгоритміне сәйкес, макрооперациялары ретінде реті nr + 1 болатын екі матрицаны көбейтуді орындайтын ns +1 макропроцессорды пайдаланып, барлық 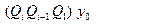көбейтулерін [log₂(s+ 1 ) ] макроқадамда есептеуге болады. Екі матрицаның көбейтіндісін табу үшін тұрғызылған параллель алгоритмді ескере отырып, биіктігі log₂ × log₂ nr және ені (nr)³s болатын барлық x₁, x₂, …, x_s векторларын есептеу үшін енді параллель алгоритмді жеңіл тұрғызуға болады. Бұл алгоритм процестің рекурренттік екіеселену атына ие болды.

Суреттелген процестің, (2.1) теңдігіндегі х_i векторларын тікелей есептеуге негізделген алгоритмнен принципиалды айырмашылықтары бар. Екі алгоритм дәл есептеулер жағдайында ғана бірдей нәтижелер береді. (2.1) сияқты рекурренттік қатынастарды қолдана отырып сызықтық алгебраның, математикалық физика және анализдің және т.б. көптеген сандық әдістері тұрғызылған. Рекуренттік екі еселену процесі егер де біз процессорлардың үлкен санын қолдана отырып, биіктігі кіші алгоритмдерді құрастыру жағынан қарайтын болсақ бұл әдістерден не күтетінімізді түсінуге жол көрсетеді. Мысалы реті n нөлдік емес үшбұрышты матрицалы сызықтық алгебралық теңдеулер жүйесі шешілуде делік. Бір параллель қадамда, шамамен n²/2 процессорларды пайдалана отырып, матрицаның барлық диагональ элементтерін 1-ге тең етуге болады. Ол үшін оларға сәйкес теңдеулердің коэффициенттерін бөлеміз. Кері қою әдісі көмегімен жүйені шеше отырып, біз бірден белгісіздер үшін (2.1) түріндегі рекурентті қатынастарды аламыз. Бұл теңдеулерде барлық матрицалар мен векторларды сандар көрсетеді, x₀ = 0, r = i, s= n. Демек, рекурренттік екіеселену процесін қолдану арқылы, үшбұрышты жүйені 0 (log₂² n) параллель қадамда, 0 (n³) процессорларды іске қоса отырып шешуге болады.

Енді, реті n квадраттық матрица А үшін кері матрицаны А^-1 есептеу тапсырмасын қарастырайық. Жылдам параллель алгоритмді құрастыру негізін келесі идея құрайды. А матрицасының характеристикалық көпмүшелігін былай белгілейік: 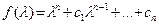. Кели-Гамильтонның теоремасына сәйкес f(А) = 0 болатыны белгілі. Сондықтан

(2.2)

Егер λ_i - характеристикалық теңдеудің түбірлері және s_k - А^k матрицаcының іздері (след матрицы) болса, онда λ_i және s_k Ньютон қатынастарын деп аталатын байланыста болады.

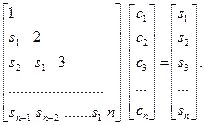(2.3)

А матрицасының кері А ^-1 матрицасын анықтаудың параллель алгоритмі келесі этаптардан тұрады. Алдымен екіеселену схемасы бойынша А матрицасының біріншісінен бастап (n - 1)-ге дейінгі барлық дәрежелері табылады. Бұл этап log₂ n макроқадамдардан тұрады және мұндағы әрбір макроқадам реті n екі матрицаның саны n /2 аспайтын көбейтулерін есептеу.

Барлық бірінші этап 0 (n⁴) процессорларда 0 (log₂² n) параллель қадамда орындала алув мұмкін. Ал екінші этапта А^к матрицаларының барлық s^к іздері 0 (log₂ n) қадамда 0 (n ²) процессорларын пайдалана отырып есептеледі. Ал үшінші этапта 0 (log₂² n) қадамда 0 (n ³) процессорларын пайдалана отырып (2.3) үшбұрышты жүйені шешу арқылы характеристикалық теңдеудің с_к коэффициенттері табылады. Ал төртінші этапта (2.2) формуласына сәйкес 0 (log₂ n) параллель қадамда 0 (n ³) процессорларын пайдалана отырып А^{- 1} матрицасы табылады. Тұтас алғанда А ^-1 матрицасын есептеудің параллель алгоритмінің биіктігі 0 (log₂² n) және ені 0 (n⁴). Дәл қазіргі уақытта осы есепті шешу үшін биіктіктері бұдан әлдеқайда кіші болатын алгоритмдер анықталмаған. Ал алгоритмнің ені азайтылуы мүмкін.

Егер реті n - ге тең квадрат А матрицалы Ах = в сызықты алгебралық теңдеулер жүйесі шешілетін болса, онда параллель алгоритм өте оңай құрылады. Жүйе шешімін х = А ^-1 в түрінде елестетіп көрейік. Алдымен, 0 (log₂² n) параллель қадамда 0 (n⁴) процессорларын қолданып А ^-1 матрицасын табамыз. Одан соң 0 (log₂ n) параллель қадамда 0 (n²) процессорларын қолданып А ^-1 матрицасы мен в векторының көбейтіндісін х = А ^-1 в, яғни шешімін табамыз.

Шексіз параллельділік концепциясы шеңберінде көптеген биіктігі кіші алгоритмдер құрастырылды. Олардың кейбіреулерін [31] жұмыста және сол тақырыптарға берілген әдебиеттерден кездестіруге болады. Сондықтан да біз оларды талдамай – ақ қоямыз. Мұның себебі: практика жүзінде бұл алгоритмдердің басым көпшілігі толық қолданыс таппаған. Оларға тән ортақ кемшіліктердің біразын айта кетсек: процессорлар сандарын көп қажет ету, операциялар арасындағы күрделі ақпараттық байланыс, сандық есептеудегі орнықсыздықтар, жадыдағы келіспеушіліктер санының көп болуы және т.б. Шексіз параллельділік концепциясының толық талдауын [10] кітаптан табуға болады. Айтылған кемшіліктерге қарамастан, кітапта біз осы концепция туралы қысқаша қарастырып кеттік.

Дата добавления: 2015-10-29