Функционалды құрылғылар жүйесі

Кезкелген есептеу жүйесі уақыт аралығында жұмыс істейтін функционалды құрылғылардың жиынтығы. Оның жұмыс сапасын бағалау үшін әртүрлі сипаттамалар енгізіледі. Оларды практика жүзінде қолдануға жеткілікті, кейбір құрылғыларының жұмыс процесінің моделі аясында қарастырайық. Біз функционалды құрылғылар орындайтын операциялардың мазмұнына үңіліп жатпаймыз, олар арифметикалық немесе логикалық функция болуы, деректерді енгізу/шығару, деректерді жадыға жіберу немесе жадыдан қайта алу т.с.с болуы мүмкін. Бізге қазір сол операциялардың орындалу уақыты және қандай типті құрылғыда іске асырылатыны маңызды.

Уақытты есептеу жүйесі және оның өлшем бірлігі енгізілді делік, мысалы, секунд. Операцияның орындалу уақыты бірлік мөлшерімен өлшенеді деп есептейік. Барлық құрылғылар, нақты немесе гипотетикалық, негізгі немесе қосымша, кезкелген қосылу уақытылы болуы мүмкін. Мұндағы бір ғана шектеу, ол – бір функционалдық құрылғының (ФҚ) барлық қосылуларының ұзақтығы бірдей болу қажет. Бізді барлық уақытта, қандай да бір нақты ФҚ жиынының жұмысы қызықтыратын болады. Осы жиындардың жұмысын қамтамасыз ету үшін қажетті басқа барлық ФҚ лезде қосылады деп есептеледі. Сол себептен, арнайы айтылмаса, мұндай жағдайда олардың нақты түрде бар екенін ескермейміз. Қарастырып отырған ФҚ-ның қосылу уақытылары нөлдік емес деп есептейік.

Егер алдыңғы операция аяқталмай тұрып, кейінгі операциялар орындалуын бастай алмаса, онда функционалдық құрылғы қарапайым деп аталады. Қарапайым ФҚ бір типті операцияларды және әртүрлі операцияларды орындай алады. Әртүрлі ФҚ операцияларды оның ішінде бірдей операцияларды да әртүрлі уақытта орындай алуы мүмкін. Қарапайым ФҚ мысалы ретінде конвейерлік сумматорлар немесе көбейтушілерді ғана келтіріп қоя алмаймыз. Бұл ФҚ операциялардың бір типін ғана жүзеге асыра алады. Қарапайым құрылғылар ретінде көпфункционалды процессорды санауымызға болады, егер де ол әртүрлі операцияларды бірмезетте орындай алмаса және біз олардың операцияларды іске асырудағы уақыт айырмашылығын назарға алмаймыз және оларды бірдей деп санаймыз. ФҚ - ның негізгі ерекшелігі біреу ғана: әрбір операцияны орындау кезінде ол өзінің құрылғыларын жеке пайдаланады.

Қарапайым ФҚ қарағанда, конвейерлік ФҚ бірнеше операцияларды бір мезетте орындау үшін өзінің құрылғыларын бөліп қояды. Әдетте оның қарапайым конструкциясы, бірдей уақытта іске қосылатын сызықты өрім сияқты қарапайым элементарлық ФҚ құралады. Осы элементарлық ФҚ, операцияның жекелеген этаптары тізбекті түрде іске асырылады. Жылжымалы үтірі бар сандарды қосу операциясын орындайтын конвейерлік ФҚ жағдайында, оған сәйкес элементтарлық құрылғылар мынадай операцияларды тізбектей іске асырады: қатарларды салыстыру, мантиссаны ығыстыру, мантиссаларды қосу және т.б. Солай болғанымен, мысалы, әмбебап процессорлардың тізбекті өрімін конвейерлік ФҚ деп есептеуге ешқандай кедергі жоқ.

Конвейерлік ФҚ-ның жұмыс істеу принципі бір қалыпта қалады. Алдымен бірінші элементарлы конвейерлі ФҚ-да бірінші операцияның бірінші этапы орындалады да нәтиже екінші элментарлы ФҚ-ға беріледі. Содан кейін екінші элементарлы ФҚ-да бірінші операцияның екінші этапы орындалады. Осы мезетте, босаған бірінші ФҚ-да екінші операцияның бірінші этапы іске қосылады. Содан соң екінші ФҚ-ның іске қосылу нәтижесі үшінші ФҚ-ға, бірінші ФҚ-ның іске қосылу нәтижесі екінші ФҚ-ға беріледі. Босаған бірінші ФҚ үшінші операцияның бірінші этапын орындауға дайын тұрады және т.с.с. Конвейердегі барлық элементарлы ФҚ-ды өту кезеңінен кейін, операция орындалды деп есептелінеді. Элементарлы ФҚ-лар конвейердің баспалдақтары (сатылары), ал конвейердегі баспалдақтар саны – конвейердің ұзындығы деп аталады. Қарапайым ФҚ-ны конвейер ұзындығы бірге тең конвейерлі ФҚ деп санауға болады. Сонымен, жоғарыда айтылып кеткендей, конвейерлік ФҚ көбіне элементарлық ФҚ-дың сызықты өрімінен құралады, бірақ бұдан да күрделі конвейерлік конструкциялар болуы мүмкін.

Конвейерлі ФҚ-ның өзі бір-бірімен байланысқан құрылғылар жүйесі болғандықтан, ФҚ жүйесі жұмысының жалпы қағидаларын орнату қажет.

Кезкелген ФҚ-ның бір мезетте операцияны орындауы және алдыңғы қосылу нәтижесін сақтай алуы мүмкін емес деп есептейік, яғни оның ешқандай да жеке жадысы жоқ. Алайда, ФҚ-да алдыңғы іске қосылудың нәтижесі, келесі іске қосылуға дейін (және осы моментті қоса алағанда) сақталуы мүмкін деп есептейік. ФҚ-да кезекті іске қосылу басталғаннан кейін алдыңғы іске қосылу нәтижесі жойылады. Барлық ФҚ дербес командалармен жұмыс істейді делік. Команда берілген мезетте нақты ФҚ-ның кірістеріне орындалып жатқан операцияның аргументтері басқа ФҚ-ның қосылуларының нәтижесі ретінде оның шығысынан беріледі немесе болмаса кіріс деректері, болмаса басқаша түрде де беріледі. Бізге қазір олардың қалай жеткізілуі маңызды емес. Маңыздысы, ФҚ-ның кезекті іске қосылу сәтінде, осы ФҚ үшін енгізілетін деректер қол жетімді болуы, ал берілу (жіберу) процесі жалпы процестің кідіріп қалуына әкеліп соқтырмауы. Әрине, біз барлық ФҚ-ның іске қосылу мезетін анықтайтын бағдарламалар дұрыс құрылып және олар тығырыққа әкеліп тіремейді деп болжам жасаймыз. Әртүрлі сипаттамаларды анықтау барысында, (ФҚ-ның жұмыс істеуімен байланысты), белгілі бір уақыт аралығында орындалатын операциялардың санын қалайда табу керек болады. Бұл сан бүтін болуы тиіс. Егер уақыт аралығыт-ға тең, ал операцияның ұзақтығы τ болса, онда Т уақыты аралығында Т/τ, болмаса (T/τ) – 1 операция орындауға болады. Уақыт аралығы Т операция ұзақтығымен τ салыстырғанда үлкен мәнге ие болған жағдайда [T/ τ ] – 1 ≈ Т/ τ тең деп алуға болады. Бұдан әрі бүтінсандылық символдары және әртүрлі реті аз мүшелермен формулалар мен жазбаларды күрделендіре бермес үшін, біз әр кезде нәтижелерді жетекшіде келтіретін боламыз, яғни ол Т 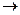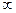шекке көшкенге эквивалентті деген сөз. Басқаша айтқанда, бұл туралы арнайы ескертілмесе де, барлық сипаттамалар мен қатынастар ассимптотикалық сипат алады. Берілген жағдай алынатын нәтижелердің практикалық маңыздылығын ешқандай төмендетпей, олардың одан әрі көрнекілігін арттырады.

Операцияның бағасы деп оның іске асырылу уақытын, ал жұмыс бағасы депбарлық орындалған операциялардың бағаларының қосындысын атайық. Берілген уақыт аралығындағы құрылғының жүктелуі (р) деп, нақты орындалған жұмыс бағасының, максималды мүмкін бағасына қатынасын айтамыз. Жүктелу р әрқашанда 0 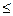р 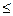1 шартты қанағаттандыратыны мәлім.

Сонымен қатар келесі айқын бекітілім орынды

Бекітілім 2.3.1

Т уақыт аралығында орындап шығуға болатын жұмыстың максималды бағасы, жай ФҚ үшін Т, ал ұзындығы n конвейерлік ФҚ үшін nT.

Құрылғылар жүйесінің н ақты өнімділігі деп бірлік уақытта орташа нақты орындалған операциялар санын айтамыз. Шекті өнімділік деп ФҚ - лар арасында байланыс болмаған жағдайдағы бірлік уақыт ішінде сол жүйеде орындалуы мүмкін максималды операциялар санын айтамыз. Анықтамадан, жүйенің нақты және шекті өнімділіктері, құрылғылар жүйесінің барлық құрамының сәйкесінше нақты және шекті өнімділіктерінің қосындысы екені шығады.

Бекітілім 2.3.2

Жалпы жағдайда қарапайым немесе конвейерлік құрылғылардан құралған жүйе s құрылғыдан тұрсын,. Егер құрылғылардың шекті өнімділігі сәйкесінше π₁,… π_s болса және р₁,...,p_s жүктелулерімен жұмыс істесе, онда жүйенің нақты өнімділігі r мына формуламен өрнектеледі.

r = 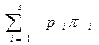(2.3.1)

Жүйенің нақты өнімділігі, барлық ФҚ - дың нақты өнімділіктерінің қосындысына тең болғандықтан, бұл бекітілімді бір құрылғы үшін дәлелдесе жеткілікті. Бір операцияны орындау үшін ФҚ - ға τ уақыт керек болсын және Т уақытта N операция орындалсын. Құрылғы типінің қандай екеніне тәуелсіз орындалған жұмыстың бағасы Nτ - ға тең. Егер құрылғы қарапайым болса, онда 2.3 1 бекітіліміне сәйкес жұмыстың максималды бағасы Т тең. Сондықтан құрылғының жүктелуі Nτ/Т тең. Анықтама бойынша ФҚ-ның нақты өнімділігі N/Т, ал оның шекті өнімділігі – 1/ τ. Енді конвейерлі құрылғының ұзындығы n тең деп алайық. Алдыңғы бекітілімге сәйкес бұл жағдайда максималды жұмыс бағасы nТ тең. Сол себептен құрылғының жүктелуі Nτ/nТ, нақты өнімділігі N/Т, ал шекті өнімділік n/τ тең. Тағы да 2.3.1 тендігі айқын.

Егер r, 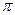, p бір құрылғының, сәйкесінше, нақты өнімділігі, шекті өнімділігі және жүктелуі болса, онда r=p 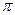теңдігі орын алады. Бұдан көретініміз, құрылғының барынша жоғары нақты өнімділігіне қол жеткізу үшін, оның барынша көп жүктелуін қамтамасыз ету керек. Тәжірибелік мақсат үшін өнімділік ұғымының маңыздылығы жоғары, өйткені тек сол ғана құрылғының қаншалықты тиімді пайдалы жұмыс істейтінін көрсетеді. Өнімділікке қатысты жүктелу ұғымы көмекші болып табылады. Оның пайдалы жағы, анықталған іс-әрекеттер арқылы өнімділікті жоғарылату жолын сілтейді. Құрылғылар жүйесі үшін де аналогты рөл атқаратын жүктелу ұғымын енгізу абзал болар еді. Оны әртүрлі жолмен анықтауға болады. Мысалы, бір ФҚ үшін сияқты, ФҚ жүйесінің жүктелуін, нақты орындалған жұмыс бағасының максималды мүмкін құнына қатысы деп есептеуге болар еді. Мұндай анықтама бізге бірнеше пайдалы қорытулар жасауға мүмкіндік туғызады. Бірақ қалыс қалулар да жоқ емес. Бұл анықтамада баяу және тез құрылғылар тең дәрежеде қалады және егер жүйенің жүктелуін көтеру қажет болса, онда оны бізге қай ФҚ-ның есебінен істегеніміз дұрыс екені бірден көрінбейді. Сонымен қатар, осы жағдайда жүйе сипаттамасына сәйкес r=p 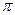теңдігі әрқашанда орындала бермейді.

Жүйе жүктелуі ұғымының дұрыс енгізу жолын (2.3.1) қатынасы береді.

Жалпы жағдайда қарапайым немесе конвейерлік құрылғылардан құралған жүйе s құрылғыдан тұрсын. Егер құрылғылардың шекті өнімділігі, сәйкесінше, π₁,… π_s болса және р₁,...,p_s жүктелулерімен жұмыс істесе, онда анықтама бойынша жүйенің жүктелуі р мына формуламен өрнектеледі.

р = 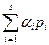, 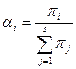(2.3.2)

Жүйе жүктелуінің өзі жеке құрылғылардың жүктелулерінің өлшенген қосындысы болып табылады, себебі (2.3.1)-ден

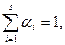
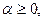
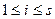(2.3.3)

екені шығады.

Сондықтан жүйе жүктелуі үшін 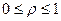теңсіздігі орындалады. (2.3.2) анықтамасынан (2.3.3) ескере отырып, құрылғылар жүйесінің жүктелуі 1-ге тең болуы үшін үшін әр құрылғының жүктелуі 1-ге тең болуы қажетті және жеткілікті екенін аламыз. Логикалық тұрғыдан бұның дұрыс екені айқын. Егер жүйе бір құрылғыдан құралса, яғни s = 1, онда (2.3.2)-ден жүйе жүктелуі және құрылғының жүктелуі ұғымдары бірдей екені шығады. Бұл факт қазіргі енгізілген, жүйенің жүктелуі ұғымы мен мұның алдында енгізілген ұғымдардың үйлесімділігінің ақиқат екенін көрсетеді.

Анықтама бойынша π құрылғылар жүйесінің шекті өнімділігі π₁ + … +π_s тең. Онда (2.3.1) (2.3.2)-ге сәйкес әрқашанда төмендегі маңызды теңдік орындалады

r = p 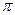(2.3.4)

Конвейерлік ФҚ-лар сияқты, ФҚ-ның санының көптігі, есепті тез шешу қажеттігі туындаған жағдайда пайдаланылады. Бізге бұны қаншалықты тез істеуге болатынын түсіну үшін жеделдік (үдеу) ұғымын енгізу керек. Жүктелу жағдайындағы сияқты, бұл әртүрлі тәсілмен енгізілуі мүмкін, және де олардың жан-жақтылығы немен және қалай салыстырылуымен байланысты. Көбінесе жеделдік (үдеу), мысалы, бір әмбебап процессорда берілген есепті шешуге жұмсалған уақыттың, сол есепті осы сияқты S процессордан құралған жүйеде шешуге кеткен уақытқа қатынасымен анықталады. Жақсы ситтуацияда жеделдік S-ке жетуі мүмкін екенін айта кетуіміз керек. Жеделдіктің S-ке қатынасын тиімділік деп атайды. Назар аударатын жағдай, жеделдіктің бұл анықтамасы аралас жүйелер үшін емес, тек бірдей құрылғылардан құралған жүйелер үшін ғана пайдаланылады. Қарастырылып отырған жағдайда «тиімділік» ұғымы жүктелу ұғымымен толық сәйкес келеді.

Алгоритм жалпы жағдайда шекті өнімділіктері, сәйкесінше, π₁,… π_s болатын қарапайым немесе конвейерлік s құрылғыдан тұратын есептеу жүйесінде Т уақытта іске ассын делік және де π₁≤ π₂ ... ≤ π_s деп есептейік. Алгоритм іске асқан жағдайда жүйенің нақты өнімділігі (2.3.1)-ден r-ге тең. Жүйе жұмысы жылдамдығын, өнімділігі жүйенің ең жылдам ФҚ-сының шекті өнімділігі π_s сияқты болатын және дәл сондай операцияларды жүйенің барлық ФҚ-дай орындай алатын қарапайым әмбебеп гипотетикалық құрылғы жұмысының жылдамдығымен салыстырамыз. Сонымен 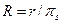қатынасын берілген жүйедегі алгоритмнің іске асырылу жеделдігі (үдеуі) немесе жай ғана жеделдік (үдеу) деп атаймыз. Гипотетикалық қарапайым ФҚ ретінде мысалы, конвейерлік ФҚ-ны таңдап алу жай емес, өйткені бір қарапайым әмбебап құрылғы кезкелген алгоритмде толығымен жүктеле алады. (2.3.1) қатынасын назарға ала отырып,

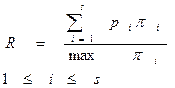(2.3.5)

қатынасын аламыз.

Жеделдікті анықтайтын (2.3.5) өрнегін талдай келе, s құрылғыдан тұратын есептеу жүйесінің жеделдігі (үдеуі), ешқашанда s- тен асып кетпейтінін және де жүйе құрылғыларының бәрі бірдей шекті өнімділікке ие болып, бәрі толық жүктелген жағдайда ғана s- ке жетуі мүмкін екенін көруге болады.

Жасалған зертеулерді қорытындылай келе, бір дербес жағдай үшін пайдалы келесі бекітілімді 2.3.3 келтіреміз.

Бекітілім 2.3.3.

Егер жүйе шекті өнімділіктері бірдей, қарапайым немесе конвейерлік s құрылғылардан құралса, онда:

· жүйенің жүктелуі барлық құрылғылардың орташа арифметикалық жүктелуіне тең.

· жүйенің нақты өнімділігі барлық құрылғылардың нақты өнімділіктерінің қосындысына тең.

· жүйенің шекті өнімділігі, бір құрылғының шекті өнімділігінен s есе үлкен.

· жүйенің жеделдігі (үдеуі) барлық құрылғылардың жүктелуінің қосындысына тең.

· егер жүйе тек қана қарапайым құрылғылардан құралса, онда оның жеделдігі сондай шекті өнімділікке ие бір әмбебап қарапайым құрылғыда алгоритмнің іске асу уақытының сол алгоритмнің осы жүйеде іске асу уақытына қатынасына тең.

Құрылғылар жүйесі жұмыс істей отырып, нақты бір өнімділікті көрсете алады делік. Егер өнімділік жеткіліксіз болса, онда оны көтеру үшін (2.3.4)-ке сәйкес жүйенің жүктелуін арттыру керек. Ол үшін (2.3.2)-ге сәйкес өз кезегінде жүктелуі әлі 1-ге тең емес кезкелген құрылғының жүктелуін көтеру керек. «Осыны біз жүзеге асыра аламыз ба» деген сұрақ туындайды. Егер құрылғы толығымен жүктелмесе, онда оның жүктелуін басқа құрылғылармен байланыста болмаса ғана ұлғайта аламыз.

Қайтадан s құрылғыдан тұратын жүйені қарастырайық. Барлық құрылғыларды қарапайым деп есептейік, себебі кезкелген конвейерлік ФҚ- ны қарапайым құрылғылардың сызықты өрімі ретінде бере аламыз. Құрылғылардың арасында бағытталаған байланыстар орнатылған және де олар жүйенің жұмыс істеу барысында өзгермейді делік. Шыңдары (төбелері) құрылғыларды, ал доғалары олардың арасындағы байланысты көрсететін бағытталған мультиграф құрастырамыз. Бір шыңнан екінші шыңға доғаны тек сонда ғана жүргіземіз, егер де бірінші шыңға сәйкес келетін құрылғының әрбір қосылуы міндетті түрде аргумент ретінде екінші шыңға сәйкес келетін құрылғының кезекті қосылуына берілсе. Бұл мультиграфты жүйенің графы деп атайық. Алдын ала жүйеге барлық бастапқы берілгендер (деректер) енгізілген деп болжайық және ол жоғарыда айтып кеткен тәртіп бойынша жұмысын бастасын. Егер жұмыс істеу барысында қандай да бір ФҚ – лар өздерінің қосылулары үшін басқа бастапқы берілгендерді талап ететін болса, онда олар ФҚ-дың кірісіне кедергісіз кешіктірілмей беріледі деп болжаймыз. Жеткілікті үлкен уақыт аралығындағы жүйенің максималды өнімділігін, яғни оның максималды мүмкін нақты өнімділігін зерттейік.

Бекітілім 2.3.4

Есептеу жүйесі шекті өнімділіктері сәйкесінше π₁,… π_s болатын қарапайым s құрылғыдан тұрсын. Егер жүйенің графы байланысты болса, онда оның максимал өнімділігі r_max келесі формуламен өрнектеледі.

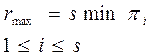(2.3.6)

Жүйе графының доғасы і- ші ФҚ-дан j- ші ФҚ-ға жүргізілді деп болжам жасайық. Жеткілікті үлкен уақытта і -ші функционалдық құрылғы Ni операция, ал j- ші функционалдық құрылғы N_j операция орындасын. і -ші функционалдық құрылғының әрбір нәтижесі міндетті түрде j- ші функционалдық құрылғының кезекті қосылуының аргументтерінің бірі болады. Сол себептен, Т- уақыт ішінде j- ші ФҚ-ның іске асырылған операциялар санының і- ші ФҚ-да іске асырылған операциялар санынан айырмасы 1 ден артық болмайды, яғни 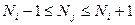. Жүйенің графы байланысты болғандықтан, ондағы кез-келген екі шың (төбе) доғалардан құралған өріммен (тізбекпен) байланысқан болуы мүмкін. Жүйенің графы q доғадан тұрады деп есептейік. 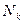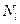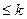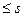Егер Т- уақыт ішінде к- шы ФҚ - операция, ал l- ші ФҚ - операция орындаса, онда соңғы теңсіздіктерден кез-келген к, l, 1 ,l үшін 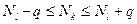екені шығады. Құрылғы

π₁≤ π₂ ... ≤ π_s болатындай етіп нөмірленген болсын.

Осы реттілікті және орындалатын операциялар саны үшін алынған қатынастарды назарға ала отырып (2.3.1)-ден аламыз

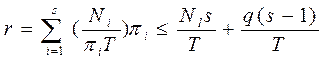
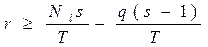
Бұл теңсіздіктердегі екінші қосылғыштар Т шексіздікке ұмтылғанда (Т →∞) 0-ге ұмтылады. Барлық k– лар үшін 1 ≤ k ≤ s мына теңсіздіктің 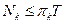орындалуы міндетті. Барлық π_k өнімділіктерінің реттелгендіктерінен және барлық N_k -дыңөзара асимптотикалық теңдігінен,егер 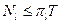теңсіздігі орындалса, онда әрбір ФҚ іске асырылатын операциялар саны асимптотикалық максимал болады. Бұл, жүйенің максимал мүмкін нақты өнімділігі асимптотикалық sπ_l тең дегенді көрсетеді, яғни (2.3.6)-пен дәлме-дәл келеді.

Салдар

Есептеу жүйесі шекті өнімділіктері сәйкесінше π₁,… π_s болатын қарапайым s құрылғыдан тұрсын. Егер жүйенің графы байланысты болса, онда:

· Құрылғылардың әрқайсысы ассимтотикалық бір ғана операциялар санын орындайды.

· кезкелген құрылғының жүктелуі ең өнімділігі төмен құрылғының жүктелуінен асып түспейді.

· егер қандай-да бір құрылғының жүктелуі 1-ге тең болса, онда ол ең өнімділігі төмен құрылғы.

· жүйенің жүктелуі келесі мәннен асып түспейді

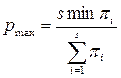
· Жүйе жеделдігі (үдеуі) келесі мәннен асып түспейді

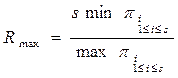
Салдар (Амдалдың бірінші заңы)

Өзара байланысқан құрылғылардан тұратын есептеуіш жүйенің өнімділігі, жалпы жағдайда, оның өнімділігі ең төмен құрылғысымен анықталады.

2.3.4 бекітілімі жүйе жұмысындағы «тар орындардың» бірін нұсқайтынын байқаймыз. Әдебиеттерде сипатталаған есептеу жүйелерінің кейбір тар орындары есептеу техникасындағы белгілі американдық маман Амдалдың атымен қалай да байланысты. Әртүрлі айғақтардың танымдылығын жоғалтып алмау үшін біз бұл салтты бұзбай, олар қарапайым болып келсе де, сәйкес бекітімдерді сол күйінде өз аттарымен қалдырамыз.

Салдар

Есептеу жүйесі қарапайым s құрылғыдан тұрсын және жүйенің графы байланысты болсын. Егер жүйе құрылғыларының шекті өнімділіктері бірдей болса, онда жүйенің асимптотикалық өнімділіігі максималды болады.

Біз максималды мүмкін нақты өнімділік туралы айтқанымызда, жүйе жұмысы құрылғылардың тұрып қалуын минималдайтын команда беру кестесімен қамтамасыз етілген деп түсінеміз.

Максималды өнімділік әртүрлі режимдерде жетуі мүмкін. Дербес жағдайда 2.3.4 бекітімі бойынша синхрондық режимде ең жай ФҚ өнімділігіне кері пропорционал тактпен жетуі мүмкін, әрине егер жүйе қарапайым құрылғылардан құралса және жүйенің графы байланысты болса. Енді өнімділігі бірдей қарапайым s құрылғыдан тұратын жүйені қарастырайық. Онда байланысты жүйедегі жағдай сияқты, байланысты емес жүйеде де, үлкен уақыт аралығында максимал мүмкін нақты өнімділік бірдей болады және бір құрылғының шектің өнімділігінің s – есесіне тең болады.

Сонымен, егер де жүйе, өнімділігі бірдей құрылғылардан тұратын болса, онда біз жүйе жұмыс істеу процесінің әртүрлі сипаттамаларының жақсарып келе жатқандығын бірнеше рет байқадық. Барлық құрылғылар, оның ішінде қарапайым және әмбебап, оларда әртүрлі операцияларды орындауға болады. Қандай да бір алгоритм осындай жүйеде іске асуда делік, ал іске асудың өзі оның қандай да бір паралельді үлгісіне сәйкес болсын. Ол туралы егжей-тегжейлі келесі параграфтарда айтатын боламыз. Бірақ бұл жерде, паралельді үлгіге де және функционалдық құрылғыларға да қатысы бар кейбір айғақтарды келтіруге ыңғайлы. Паралельді үлгінің биіктігі m -ге, ал ені q -ға тең, және алгоритмде барлығы N операция орындалады делік.

Бекітілім 2.3.5

Келтірілген шарттарда жүйенің максималды мүмкін жеделдігі (үдеуі) N/m – ге тең.

Есептеу жүйесі шекті өнімділіктері π болатын s құрылғыдан тұрсынделік. Алгоритмнің Т уақыт іске асуы аралығында і -ші ФҚ-да N 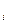операция орындалады деп болжайық. Анықтама бойынша і -ші ФҚ-ның жүктелуі 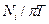-ға тең. Бұл жағдайда (2.3.5)-ке сәйкес жүйенің жеделдігі (үдеуі) тең болады

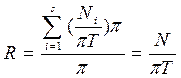
Құрылғылардың берілген өнімділігіне сәйкес параллельді үлгінің бір ярусының іске асу уақыты 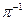-ге тең. Сондықтан алгоритмнің іске асу Т уақыты m/n –нен кем болмайды және де егер барлық ярустар кедергісіз бірінен соң бірі іске асса осы шамаға жетеді. Яғни, жүйенің жеделдігі, құрылғылардың санына байланыссыз N/m- нен аспайды.

Салдар

Максималды мүмкін жеделдікке қол жеткізуге болатын жүйе құрылғыларының минимальды саны, алгоритмнің еніне тең.

Қандай да бір себептермен N операцияның n –ін біз тізбектеп орындауға мәжбүрміз деп болжайық. Бұған әртүрлі себептер болуы мүмкін. Мысалы, операциялар ақпаратты тізбекті байланыста болуы мүмкін. Мұнда да алгоритмді өзгертусіз оларды басқаша іске асыруға болмайды. Бірақ мынадай болуы мүмкін, біз жай ғана осы операциялармен сипатталатын алгоритмнің осы бөлігіндегі паралельділікті анықтай алмадық. 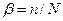қатынасын тізбекті есептеулер еншісі (долясы) деп атайық

Салдар (Амдалдың екінші заңы)

Жүйе бірдей s қарапайым әмбебап құрылғылардан құралған болсын. Алгоритмнің паралельді бөлігін орындау кезінде барлық s құрылғы толығымен жүктеледі деп болжам жасайық. Онда максималды мүмкін жеделдік R тең болады:

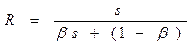(2.3.7)

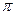арқылы жеке ФҚ-ның шектік өнімділігін белгілейік. 2.3.3 бекітілімініе сәйкес

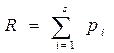
Егер барлығы N операция ғана орындалатын болса, онда олардың ішінде s құрылғының әрбірінде 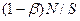операциядан 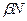операция тізбектеліп және 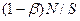операция параллель орындалады. Жалпы, барлық тізбектеліп орындалатын операциялар бірінші ФҚ-да орындалады деп есептеуге болады. Алгоритмнің іске асу уақыты

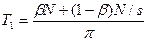
Алгоритмнің параллельді бөлігіне бірінші және сол сияқты қалған барлық құрылғылар да жұмыс істейді және оған T_i уақыт жұмсалады

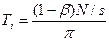
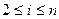үшін. Сол себептен 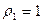және

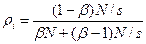
Яғни

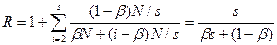
Салдар (Амдалдың үшінші заңы)

Жүйе қарапайым бірдей әмбебап құрылғылардан құралсын делік. Кез-келген жұмыс режимінде оның жеделдігі тізбекті есептеулер еншісінің кері шамасынан асып түсе алмайды.

Соңғы салдардан байқайтынымыз келесі ғана, егер n операция тізбектеліп орындалса, онда алгоритмнің кезкелген параллель үлгісінің ярустар саны n -нен кіші болмайды. 2.3.5 бекітілімінің белгілеулерінің шарты бойынша m 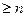дегенді білдіреді.

Жүргізілген зерттеулерде операцияның мазмұны жайында анық айтылған жоқ. Жалпы жағдайда, олар қосу және көбейту сияқты элементарлық немесе күрделі есептерді шешуге арналған үлкен алгоритмдер болуы мүмкін.

Жаңа заманғы есептеуіш жүйелер мыңдаған, он мыңдаған, жүз мыңдаған процессорлардан құралады. Процессорлар саны көп жүйелер жеткілікті түрде толығымен жүктелуі керек. Кері жағдайда оларды құрудың еш мәні жоқ. Осындай жүйелерде іске асырылатын алгоритмдердегі тізбекті операциялардың еншісі пайыздың оннан бір немесе жүзден бір бөліктерін ғана құрау керек. Алгоритмдерді құрастыру мәселелеріне келесі бөлімде тоқталатын боламыз.

Қорыта келе келесілерді атап өтейік. Параллельді процестер және параллель есептеу жүйелеріне арналған жан-жақты әдебиеттерде, өнімділік, жеделдік, тиімділік және т.с.с қатысты көптеген әртүрлі анықтамалар мен заңдылықтарды кездестіруге болады. Әдетте, жаңа анықтамалар мен заңдар, олардың ескі нұсқалары зерттеушілерді қандай да бір себептермен қанағаттандырмаған жағдайларда туады. Бірақ мұндай «жаңашылдыққа» өте сақтықпен қарау керек екенін естен шығармаған абзал.

Амдал формуласын негізінен жеделдету мүмкіндігін болжау үшін қолданған жөн. Берілген жағдайда, 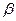шамасын программаны паралельді есептеу жүйесінде жібермей ақ есептеуге болады. Густавсон–Барсис формуласын программаныбір процессорлы компьютерлерде жібермей ақ қол жеткізілген жеделдікті бағалау үшін қолдануға болады [5]. Мұнда 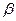шамасы есепті шешу процесінде өлшенбейді.

Сұрақтар мен тапсырмалар.

1. Неге конвейерлік ФҚ-ның бөлек сатыларының іске қосылу уақыт аралықтары бірдей болатындай етіп жасалынады?

2. Есептеу жүйесінің графы барлық доғалары бір бағытқа бағытталған, мысалы, сағат стрелкасымен ориентирленген сақина болсын. Жүйе жұмыс істей алатындай әртүрлі «уақыт» режимдері бар екенін көрсетіңіз.

3. 2-ші пункт шартына сәйкес кірістік деректер берілгендер жағдайында әртүрлі уақыт режимдері бірдей нәтижеге жеткізетінін дәлелде.

4. 2-ші пункт шартына сәйкес есептеу жүйесінде іске асырылатын алгоритм бір-біріне тәуелсіз есептеу бұтақтарына бөлінетінін дәлелдеңіз.

5. 2-ші пункттегі алгоритм қанша бұтаққа бөлінеді?

6. Жеке бұтақтар арасында ортақ не бар?

7. Енді есептеу жүйесінің графы, төбесі ортақ бағытталған әртүрлі өлшемдегі екі сақинадан тұрсын. Жүйе жұмыс істей алатындай әртүрлі «уақыт» режимдері бар (жоқ) екенін көрсетіңіз.

8. 7-ші пункт шартына сәйкес кірістік деректер берілгендер жағдайында әртүрлі уақыт режимдері бірдей (әртүрлі) нәтижеге жеткізетінін көрсетіңіз.

9. 7-ші пункт шартына сәйкес есептеу жүйесінде іске асырылатын алгоритм бір-біріне тәуелсіз есептеу бұтақтарына бөлінетінін (бөлінбейтінін) көрсетіңіз.

10. 7-ші пункттегі алгоритм қанша бұтаққа бөлінеді?

11. Егер есептеу жүйесінің графы бір жолдан тұрса, онда 2-6 подпункттердегі жауаптарда не өзгереді?

Дата добавления: 2015-10-29