Ішкі параллельділік

Тізбекті компьютерлерді ұзақ уақыт бойы пайдалану процесінде сандық әдістердің және бағдарламалардың үлкен көлемі жинақталып және олар терең меңгерілді. Параллель компьютерлердің пайда болуы жаңа әдістердің де пайда болуына әкелуі керек сияқты болатын. Бірақ олай болмады. Арнайы параллель әдістерді құрастыру әрекеті, мысалы, кіші биіктік әдісі практика жүзінде өз орнын таппады, орындалмады. Онда әрине, параллель компьютерлерде қалай есептерді шығаруға болады, және оларда ескі алгоритмдік және бағдарламалық багажды қолдануға болады ма деген сұрақ туындайды? Бұл сұрақтың жауабы, формасына қарай қарапайым болғанымен, жүзеге асырғанда қиын болып табылды және ол келесідей болды.

Математикалық қатынастар түрінде, тізбекті бағдарламалар немесе қандай да бір басқаша әдіспен жазылған жарамды кезкелген алгоритмді алайық. Осы жазба бойынша ол үшін алгоритм графын тұрғызу мүмкін болды делік және де бұл граф үшін ярустарының ені жеткілікті шамада болатын параллельді форма табылды деп есептейік. Онда қарастырылып отырған алгоритмді параллель компьютерде іске асыруға болады. Өте маңызды айта кететін жайт, 1.2.2бекітіліміне сәйкес алгоритмнің параллель іске асырылуы, кезкелген басқалары сияқты есептеу қасиеттеріне ие болады. Дербес жағдайда, егер бастапқы алгоритм сандық жағынан тұрақты болса, онда ол параллель формасында да осындай қалпында қала береді. Алгоритмдердегі осы сияқты паралллельділік ішкі деп аталады.

Ескі, яғни көптен бері қолданыстағы және жақсы меңгерілген алгоритмдерде ішкі параллельділік қорын жиі кездестіруге болады екен. Ішкі параллельдікті қолданудың көп артықшылықтары бар, себебі жаңадан құрастырылған алгоритмдердің есептеу қасиеттерін оқып-үйренудің, ол үшін қосымша күш салудың қажеті жоқ. Кемшіліктері де бар - ол алгоритмдердің графын анықтау және оларды зерттеу қажеттілігі. Кейбір жағдайларда, мысалы қандай да бір алгоритмнің ішкі параллельдігі нақты бір паралллель компьютерді тиімді пайдалану үшін жеткіліксіз болса, онда оны басқа параллельділік қасиеттері жоғары алгоритммен алмастыруымызға тура келеді. Қуантарлығы, бүгінгі күнге дейін өте көп есептер үшін үлкен көлемде әртүрлі алгоритмдер құрастырылып қойылған. Сол себепті қажетті алгоритмді таңдап алу мүмкіндігі әрқашанда болады десек артық болмайды. Бірақ мұндай таңдауды іске асыру әрқашанда оңай бола бермейді, себебі алгоритмнің параллельдік құрылымын жақсы білу керек. Ал ол болса белгісіз. Сондықтан, алгоритмнің параллель қасиеттері, құрылымы туралы мәліметтердің, және осы мәліметтерді алуға мүмкіндік беретін білімнің қаншалықты өзекті мәселелер екені түсінікті.

Бірнеше мысал қарастырып көрелік.

1 мысал. Берілген реті n болатын екі В, С квадрат матрицаның көбейтіндісін А=ВС есептеудің классикалық есебін қарастырайық [8]. А, В, С матрицаларының элементтерін сәйкесінше a_ij, b_ik, c_kj деп белгілейік, және олар сандар болсын. Матрицаларды көбейту операциясының анықтамасына сәйкес

(2.4)

Бұл формулалар А матрицасының элементтерін тікелей есептеуде жиі қолданылады. Өздігінен олар алгоритмді бірмәнді (однозначно) анықтамайды, себебі қосу таңбасының астындағы 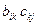көбейтіндісін қосудың реттілігі анықталмаған. Бірақ есептеудің параллельдігі анық көрініп тұрғанын байқаймыз. Ол i, j индекстерінің қандай да болса іріктеу реттілігі сақталуы туралы нұсқаудың (ереженің) жоқтығымен көрсетіледі.

Егер сандарды қосу және көбейту операциялары дәл орындалса, онда (2.4) – теңдігіндегі қосудың барлық реттері эквивалентті және олардың бәрі бір нәтижеге алып келеді. Қандай да бір ойлардың нәтижесінде (2.4) формуласын іске асырудың келесі алгоритмі таңдалған делік:

(2.5)

Тағы да i, j индекстерін іріктеу параллельділігі анық көрсетілген. Бірақта к индексі бойынша паралллельділік жоқ, себебі (2.5)–тің ортаңғы формуласынан көріп отырғанымыздай, ол индекс 1-ден бастап n -ге дейін тізбекті түрде іріктелуі керек.

Енді (2.5) алгоритмінің графын тұрғызайық. Граф төбелері a + bс түріндегі операцияларға сәйкес келеді деп есептейміз. Мұндағы a, b, с сақинаның (дөңгелектің) элементтері, және А, В, С матрицаларының элементтері сол дөңгелекке тиесілі. Көрнекілік үшін оларды сан ретінде қарастырса да болады, бірақ олар мысалы, реті бірдей квадрат матрицалар болуы да мүмкін. Графты тұрғызу барысында a, b, с элементтерінің табиғатын ескермейміз. Алғашында графта В, С матрицалары элементтерінің ендірілуімен және А матрицасының элементтеріне есептелінген a_ij⁽ⁿ⁾ мәндерін беруге байланысты болатын төбелерді және оларға инцидентті доғаларды да көрсетпейміз. Алгоритм графының зерттелуіне ақталмаған қосымша қиындықтарды ендірмес үшін, граф төбелерін еркін түрде орналастыруға болмайды. Оларды орналастырудың қолайлы да тиімді тәсілін (2.5) формуласының жазылу түрі көрсетіп тұр десе болады. Тік бұрышты торды үшөлшемді кеңістікте i, j, к координаталарымен қарастырайық. Тордың барлық бүтінсанды тораптарына 1 ≤ i, j, к ≤ n үшін граф төбелерін (шыңдарын) орналастырамыз. (2.5) формуласын талдай отырып, координаталары i, j, к болатын төбеге к > 1 үшін, координаталары i, j, к - 1 болатын төбеге сәйкес келетін операцияның орындалу нәтижесі берілетініне көз жеткізу қиын емес.

37 сурет. Матрицаларды көбейту графы

Алгоритм графы жеткілікті дәрежеде қарапайым тұрғызылған. Ол n² өз ара байланыспаған подграфтарға ыдырайды. Әрбір подграф к осіне паралллель орналасқан бір жолды көрсетеді және n төбеден тұрады. Күткеніміздей, (2.4) және (2.5) жазбаларындағы анық көрсетілген сол параллельділік осы графта да көрсетілген. Алгоритм графы n = 2 үшін 37, а суретте келтірілген. Толық графта мәліметтерді көптеп жіберу кездеседі.

b_ik элементтері координаталарының мәндері i, k болатын барлық төбелерге, ал с_kj - координаталарының мәндері k, j болатын барлық төбелерге жіберіледі. n = 2 үшін бұл таратылым 37, б-суретте келтірілген. Графтың барлық төбелері a+bс түріндегі операцияларға сәйкес келеді. Бірақ k = 1болғанда олар k ≠ 1қарағанда бірсыпыра басқаша орындалады. Осы жағдайда а аргументі қандайда бір операцияның нәтижесі болмайды, ал әрқашанда 0-ге тең деп алынады. k = 1болғанда 0-ді алгоритмнің кіріс дерегі деп алып, оны барлық төбелерге таратылуына еш кедергі болмайды.

Бұл мысал алгоритм графы төбелерін орналастырудың дұрыс тәсілін таңдаудың қаншалықты маңызды екенін жақсы көрсетеді. Егер, мысалы, төбелерді түзу сызық бойына орналастырса және олар (2.5)-гі i, j, к индекстерімен ешқандай байланыссыз болса, онда бұндай графта параллельділікті байқау сірә мүмкін емес те болар. Төбелердің таңдалған орналастырылуы бойынша паралллельділік айқын. Олай болса кезкелген паралллель форманың кезкелген ярусын (қабатын) жеңіл көрсетуге болады. Бұл дегеніміз бекітілген i, j кезіндебір төбеден артық кірмейтін төбелер жиыны. Канондық параллель форманың ярустары k = constгипержазықтығында жататын төбелер жиынын құрайды. Сондықтан, төбелерді орналастыру тәсілін алгоритмнің жазылуында пайдаланылатын индекстер жүйесімен байланыстыруға тура келетіні айқын. Берілген, яғни матрицаларды көбейту мысалы мұндай тәуелділікті анық көрсетіп тұр.

Егер (2.4) өрнегіндегі қосындыны екіеселену схемасы бойынша орындайтын болсақ, онда алгоритм графы мүлдем бөлек болатынын байқаймыз. Бұл жағдайда 37, а – суретіндегі графтың әрбір жолы, 36 - суреттегі төменгі графқа ауыстырылуы керек. Енді жаңа графты үш өлшемді кеңістікте орналастыру қиындау болады. Екіеселену қағидасын қолданып (бір индексті пайдаланып) қосындыны жазу да айтарлықтай қиыншылықтар туғызады.

2 мысал. Енді Аx=b түріндегі сызықты алгебралық теңдеулер жүйесін кері қою әдісі көмегімен шешу жолын қарастырайық. Мұндағы А реті n үшбұрышты анықтауышы нөлге тең емес квадрат матрица. a_ij, b_i, x_i арқылы сәйкесінше матрицаның элементтерін, жүйенің оң жағын және шешім-векторын белгілейміз. Түсінікті болу үшін А матрицасын диагоналдық элементтері 1-ге тең сол жақ үшбұрышты деп алайық. Онда

(2.6)

Қосу реті анықталмағандықтан, бұл өрнек те алгоритмді бірмәнді анықтамайды. Мысалға, j индексінің өсуіне қарай тізбекті қосуды қарастырайық. Сәйкес алгоритмді келесі түрде жазуға болады

(2.7)

Алгоритмнің ең негізгі операциясы a-bс түрінде берілген. Бұл барлық мүмкін болатын i, j индекстерінің мәндері үшін орындалады. Қалған операциялардың барлығы меншіктеуді орындайды. Мұнда да алгоритм графын тұрғызу кезінде операцияларды қарапайым қайта нөмірлеу тиімсіз екені көрінеді. Декарттық координат жүйесінде (i, j өстерімен) қадамы 1-ге тең болатын тікбұрышты координаталық торды тұрғызайық және тор тораптарына (түйіндеріне) a-bс операцияларына сәйкес келетін 2 ≤ i ≤ n, 1 ≤ j ≤ i -1 үшін граф төбелерін орналастырайық. Операциялар арасындағы байланысты талдай отыра, алгоритм графын тұрғызамыз және оған кіріс a_ij және b_i, деректерін білдіретін төбелерді енгіземіз. Бұл граф n =5 жағдайы үшін 38, а - суретте көрсетілген. Жоғарғы бұрыштағы төбе i=1, j= 0 координаталы нүктесінде орналасқан.

38 сурет. Үшбұрышты жүйелерге арналған графтар

Бұл суретте параллельді форманың ең максималды түрінің бірі көрсетілген. Оның ярустары пунктирлі сызықтармен белгіленген.Егер a_ij элементтерінің енгізілуіне сәйкес келетін төбелерді бірінші яруске орналастырса, онда параллельді форма канондық болады. а — bс түріндегі операциялар енетін ярустардың жалпы саны n - 1 тең. Бірінші яруста b векторының элементтерін енгізу операциялары орналасқан.

Егер (2.6) өрнегіндегі қосындыны есептеуде біз қандай да бір оймен қосудың тізбекті әдісіне тоқтаған болсақ, онда j индексінің өсуі бойынша қосуды таңдау жалпы кездейсоқ жасалған болатын. Бұл таңдаудың қандай да бір артықшылықтары көрініп тұрмағандықтан кері қоюдың алгоритмін j индексінің кемуі бойынша қосу арқылы тұрғызуға болады. Онда оған сәйкес алгоритм келесі түрде болады:

(2.8)

Оның графы n = 5 жағдайы үшін 40, б-суретте көрсетілген. Енді жоғарғы бұрыштағы төбекоординатасы i = 1, j = 1 болатын нүктеде орналасады. Қандай да бір параллель форманың ярустарына a - bс түріндегі операцияларға сәйкес келетін төбелерді орналастыра отырып, ондағы әрбір яруста әрқашанда тек бір төбе ғана бола алатынын байқаймыз. Бұл 40-шы суретте графтың барлық төбелері бір жолда жатуымен түсіндіріледі. Бұл жол пунктирлі бағыттармен көрсетілген. Сондықтан (2.8) алгоритмі графындағы a – bc түріндегі операцияларды қамтитын ярустардың жалпы саны әрқашан (n² – n + 2)/2 тең болады, бұл (2.7) алгоритмі графындағы n -1 ярустар санына қарағанда әлдеқайда көп.

Күтпеген нәтиже алынды десе болады. Шынында, екі алгоритм де (2.7) және (2.8) бір ғана есепті шешуге арналған, олар (2.6) бірдей формулалары негізінде құрылған және дәл есептеулерге қатысты алсақ эквивалентті. Екі алгоритм де бірдей жады көлемін және азайту, көбейту операцияларының бірдей санын талап ететіндіктен, бірпроцессорлы компьютерлерде іске асырылу жағынын алғанда олар бірдей.

Дегенмен, екі алгоритм графтарының бір-бірінен айтарлықтай айырмашылығы бар. Егер бұл алгоритмдерді n әмбебап процессордан тұратын параллель есептеу жүйесінде іске асырса, онда (2.7) алгоритмін n- ге пропорционал уақыт ішінде, (2.8) алгоритмін тек n ²-қа пропорционал уақыт ішінде іска асыруға болады. Бірінші жағдайда процессорлардың орташа жүктелуі 0,5-ке, екінші жағдайда 0-ге жуық болады.

Сонымен, қарапайым компьютерлерде іске асырылуы жағынан қарағанда бірдей болатын алгоритмдер, параллель компьютерлерде іске асырылу кезінде мүлдем әртүрлі болулары мүмкін. Осы мысалды қолдана отырып айта кететін нәрсе, параллель компьютерлерді математикалық тұрғыдан игерудің басты қиындықтары да осы фактінің негізінде жатыр. Көптеген жылдар бойы «қарапайым» компьютерлерде жұмыс істейтін әртүрлі мамандық иелері, алгоритмдерді негізінен олардың 3 сипаттамасы бойынша бағалайды: операция саны, талап етілетін жадының көлемі және дәлдігі. Осы сипатттамалар негізінде барлығы дерлік тұрғызылды: есептеу техникасының негізгі параметрлері, есептеу ісіне үйрету процесі, есептеу әдістері және алгоритмдерін құрастыру, тиімділікті бағалау, тілдерді және трансляторларды құрастыру және көптеген т.б. Параллель есептеу жүйелерін құруда, алгоритмдерден, принципиалды түрде басқа қасиеттері мен сипаттамалары талап етілді, ал оларды білу тізбекті компьютерлер үшін қажеті де болмаған еді. Сонымен алгоритмдерді тереңірек зерттеу, олардың параллель қасиеттерін оқып үйрену, параллельділікті анықтау үшін конструктивті әдістемелігін құрастыру қажетті де маңызды іс-шаралардың қатарына жатады.

Математикалық физика теңдеулерін торлар әдістерімен шешу кезінде пайда болатын сызықты алгебраның көптеген есептерінің ішінде, блокты-екідиагоналды матрицалы сызықты алгебралық теңдеулер жүйесін шешу есебі жиі кездеседі. Мұндағы диагоналдық емес блоктар диагоналды матрицалардан тұрады, ал диагональ бойындағы блоктар – екідиагоналды матрицалар. Анығырақ болу үшін, жүйенің матрицасы сол жақты үшбұрышты болсын деп есептейік. Матрицаның блоктық реті m, алблок реті n болсын. Сонымен, Au = f түріндегі сызықты алгебралық теңдеулер жүйесін қарастырайық [10].

мұндағы

(2.9)

Егер U₀ = 0, D₀ = 0 деп алатын болсақ, блокты – екідиагоналды жүйенің (2.9) шешімі рекуррентті анықталады:

U_k = B_k^-1(F_k – D_k-1U_k-1), 1 ≤ k ≤ m (2.10)

Х = В^-1(F — DY) макрооперациясы, F, Y векторлары және В, D матрицалары бойынша Х векторын есептейді. Әрбір төбесі осы макрооперацияға сәйкес келеді деп есептей отырып, (2.9) алгоритмінің графын тұрғызамыз. Ол 39-шы суретте көрсетілгендей болады. Төбелердің және доғалардың үлкен көлемі, бұл операциялардың күрделілігін және күрделі ақпарат берілетінін көрсетеді.

39 сурет. Блокты-екідиагоналды жүйеге арналған Макрограф

Граф құрылымынан көрініп тұрғандай, егер (2.10) алгоритмін векторлы-матрицалық операциялар тізбегі ретінде қарастыратын болсақ, онда ол тізбекті болады және ол параллельденбейді. Іс жүзінде жеке алғанда әрбір макрооперация параллельденбейді. Сонымен бірге ол екідиагоналды жүйенің шешімін береді. Сондықтан, жүйенің оң жақ бөлігін есептеу процесі ғана параллельденуі мүмкін, егер де әрине жүйені (2.10) сияқты қайта шешетін болса.

Бұл фактілерден, қарастырылып отырған (2.9) жүйені шешу алгоритмін жақсы параллельдеу мүмкін емес деп қорытынды жасауға болар еді. Алайда бұндай қорытынды жасау асығыстық болады.

Блокты-екідиагоналды жүйені шешу алгоритмін зерттеп көрелік Алгоритмнің полиэлементті. Берілген матрица элементтері мен векторлардың жоғарыдағы жасалған белгілеулерін ескере отырып алатынымыз:

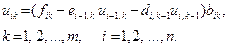(2.11)

Бұл жағдайда барлық i, k үшін 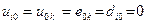деп алынады. (2.11) формуласында b,f, e, x, d, y шамалары бойынша u шамасын есептейтін ең басты және жалғыз скалярлы операция

и=b^-1(f - ex - dy), (2.12)

Тағы да операцияны тиімсіз қарапайым қайта нөмірлеу. Алгоритм графын тұрғызу үшін тік бұрышты тор қарастырамыз және оның түйіндерінің (тораптары) координаталары i, к бүтінсанды деп алайық. Тордың барлық түйіндеріне 1 ≤ i ≤ n, 1 ≤ к ≤ m үшін граф төбелерін орналастырамыз және оларды (2.12) операцияларына сәйкес келеді деп санаймыз. Кіріс деректерімен және кейбір аргументтердің нөлдік мәндерімен жабдықтайтын төбелерді көрсетпейміз.

(2.11) өрнегін талдай келе,координатасы i, k болатын төбегекоординаталары i - 1, k және i, k - 1 болатын төбелер сәйкес келетін операциялардың орындалу нәтижелері берілетініне көз жеткізу қиын емес. Координаталары i, k болатыноперацияны іске асыруға қажетті қалған барлық деректер кіріс деректері болады және тек осы операцияны жүргізу үшін ғана керек. Бұл алгоритм графында (2.5) алгоритміндегі сияқты кіріс деректерін көптеп жіберу жоқ. n = 5, m = 9 болғанжағдайдағы алгоритм графы 40-шы суретте көрсетілген. Одан алгоритм графы өте жақсы параллельденетінін көреміз. Максималды параллель форманың ярустары пунктирлі сызықтармен белгіленген. Кіріс деректерінің енгізілуін ескермеген кездегі алгоритмнің биіктігі m + n +1,алгоритмнің ені min(m, n).41-суретте осы графтың төбелері пунктирлі сызықтармен біріктірілген. Осындай әрбір топ (бөлік) 39-шы суретте келтірілген графтың бір төбесіне сәйкес. Олар жалпыланған паралллель форманың ярустары болып табылады. Осы суреттерден жақсы параллельденетін алгоритмнің өзі операцияларды сәтсіз үлкейткенде қалай параллельденбеуі мүмкін екені көрініп тұр.

40 сурет. Блокты-екідиагоналды жүйеге арналған граф

41 сурет. Жалпыланған пралллель форманың ярустары

Мысал 3. Бірөлшемді жылу өткізгіштік теңдеуі үшін шектік есебін шешу жолын қарастырайық. Бізден u (у, z) шешімін табу талап етілсін,

мұндағы

h қадамымен z және τ қадамымен у бойында бірқалыпты тор тұрғызайық. Қандай да бір себептерге байланысты айқын схема таңдап алынды делік.

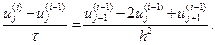
Алгоритм келесі формулаға сәйкес іске асырылатын болсын.

(2.13)

Алгоритм графын тұрғызу үшін i, j остерімен тік бұрышты координат жүйесін енгізейік. Берілген айнымалылар z, у және i, j арасындағы байланыс

қатынасымен беріледі.

Бүтінсанды тордың әрбір торабына граф төбесін орналастырамыз және оны a, b, c аргументтерінің әртүрлі мәндері үшін орындалатын келесі скаляр операцияға сәйкес келеді деп есептейміз.

(2.14)

Алгоритм графы h = 1/8, τ = Т /6жағдайы үшін 42 а, б - суретінде көрсетілген. Облыс шекарасында төбелер орналасқан, олар бастапқы деректердің және шектік мәндердің енгізілуін білдіреді.

Бұл мысалда алгоритмдердің кезкелген компьютерде іске асырылуына қатысты өте маңызды сұрақ та қарастырылады. Бұған дейін біз оны операциялардың параллельді форманың қабаттары бойынша орындалуымен байланыстырған болатынбыз. Әрине, бір қабаттың операциялары бір-біріне тәуелді емес және оларды әр түрлі құрылғыларда бір мезгілде орындауға болады. Бірақ, параллель есептеуді осылай ұйымдастырудың тиімділігі өте төмен болуы мүмкін. 42, а – суретте, (2.13) алгоритмінің максималды параллель формасының барлық ярустары пунктирлі сызықтармен көрсетілген. Операциялар осы ярустар бойынша орындалады делік.

Бір ярустың (2.14) түріндегі әрбір операциясы үш аргументті талап етеді. Олар алдыңғы яруста орындалған операциялардың нәтижелері болып табылады. Егер, бір яруста алынған деректердің жадыдан тез алынуы мүмкін болса, онда алгоритмді параллель форманың ярустары бойынша іске асыруда ешқандай маңызды қиыншылықтар туындамайды. Дегенмен, үлкен көпөлшемді есептер үшін ярустар үлкен масштабты болып, олар туралы ақпарат жылдам жадқа сыймай қалуы мүмкін. Онда оларды орналастыру үшін баяу жадты пайдалануға тура келеді. Бұл жады үшін бір санның таңдалу уақыты (2.14) базалық операциясының орындалу уақытынан әлдеқайда асып түседі. Ол дегеніміз кезекті ярусқа өту кезінде операцияны орындауға жұмсалған уақыт жадымен өзара қатынас уақытынан біршама аз уақытты алуы мүмкін дегенді білдіреді. Операцияның орындалу уақытының жадыға қатынау уақытына қатынасы неғұрлым аз болса, параллель форманың ярустары бойынша (2.13) алгоритмін іске асырудың тиімділігі соғұрлым төмен болады. Бұл жағдайда, параллель компьютердің жұмыс уақытының басым бөлігі есептеуге емес, баяу жадпен деректер алмасуға жіберіледі.

42 сурет. Графтағы микро және макропараллельділік

Қандай да бір тәсілдермен (2.13) алгоритміндегі баяу жадтың қолданылу тиімділігін арттыруға болады ма, егер болса қалай? Бұл сұрақтың жауабын алгоритм графын тереңірек зерттеу арқылы ала аламыз. Алгоритм графында 42, а горизонталь ярустарымен параллель формадан бөлек, көлбеу ярустарымен жалпыланған параллель формалар да бар. Мысалы жалпыланған параллель формаларды i + j = const және i - j = const түзулерінде ярустарға төбелерді жинақтау арқылы алуға болады. Осындай ярустардың кейбірі 42, б-суретте пунктирлі сызықтармен көрсетілген. Белгіленген ярустар графтың берілу облысын көпқырларға бөледі. Енді (2.13) алгоритмін алынған көпқырлар бойынша параллель іске асыруға болады. Сонымен қатар, бір көпқырға қатысты барлық операциялардың орындалуы барлық уақытта бір процессорға жүктеледі. Параллель орындалу кезінде ең алдымен 44, б-суретіндегі штрихталған төмендегі көпқырларға сәйкес операциялар орындалады. Одан кейін жанындағы көрші штрихталмаған көпқырларға сәйкес келетін операциялар параллель орындалады және т.с.с.

Жаңа процесте бір көпқырдың операциялары макрооперацияға айналады. Макрооперацияның орындалу уақыты көпқырдағы төбелердің санымен анықталады, ол шамамен көпқырдың ауданына пропорционал. Көпқырлар өзара ақпараттық байланысты шекара маңында жатқан төбелер арқылы жүзеге асырады. Яғни, макрооперацияның орындалуы үшін қажетті ақпаратты жадтан алу уақыты, көпқырдың шекарасының ұзындығымен анықталады. Көпқырлардың өлшемдерін еркін таңдауға болады. Олар тек жалпыланған параллель формалардың қандай ярустары олардың шекараларын құрайтынына байланысты болады.

Әрқашанда графтың берілу облысын бөлуді, ондағы көпқырлардың басым көпшілігінің шекара ұзындықтарының олардың аудандарына қатынастары өте аз болатындай етіп таңдауға болады. Бұндай макрооперациялардың орындалуы кезінде баяу жадқа қатынасу уақытының әсері өте қатты төмендейді.

Осы уақытқа дейін алгоритмдердің параллель формалары негізінен тәуелсіз операциялардың жиынын анықтау үшін қолданылып келді десе болады. Осы мысал көрсеткендей, олар баяу жадтың тиімді пайдаланылу мүмкіндіктерін зерттеу үшін де пайдасы болуы мүмкін екені анық. Айта кету керек, жоғарыда жасалған ой, пікірлер параллель компьютерлер және кәдімгі қарапайым компьютерлер үшін де бірдей орынды болады.

Жоғарыда қарастырылған мысалдар көрсеткендей, көптеген алгоритмдерде шынында да параллельділіктің үлкен қорлары бар. Параллельділікті анықтау үшін немесе оның жоқ екенін бекіту үшін алгоритмдердің графтарын және олардың параллель формаларын білу үлкен роль атқарады. Сонымен қатар, алгоритмдер графтарын және олардың параллель формаларын, компьютерлерде (параллель болуы міндетті емес) алгоримдерді іске асыруға қатысты көптеген басқа сұрақтарды шешу үшін де тиімді қолдануға болатыны белгілі.

---

Дата добавления: 2015-10-29