Часть 3.2. Система шестого порядка

Структурная схема двухконтурной системы управления ДПТ НВ с ПИ-регуляторами скорости и тока, а также апериодическим входным фильтром приведена на рис. 52.

Рис. 52. Структурная схема двухконтурной системы управления ДПТ НВ с ПИ-регуляторами скорости и тока, а также апериодическим входным фильтром

Представленная САУ ДПТ имеет шесть переменных состояния: скорость вала двигателя, ток якоря двигателя, выходное напряжение тиристорного преобразователя, представленного апериодическим звеном 1-го порядка, интегральная составляющая выходного напряжения ПИ-регулятора тока, интегральная составляющая выходного напряжения ПИ-регулятора скорости, а также выходное напряжение апериодического фильтра.

Соответственно, математическое описание электромеханической системы можно представить в виде системы из шести дифференциальных уравнений первого порядка. Рассмотрим составление этих уравнений, начиная с выходной координаты электропривода и двигаясь последовательно к началу системы.

Динамику изменения скорости вала двигателя описывает дифференциальное уравнение движения:

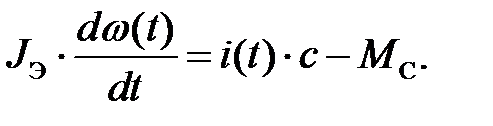
Уравнение равновесия напряжений для якорной цепи двигателя:

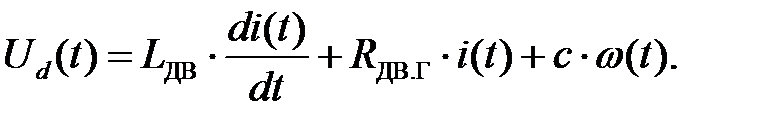
Для составления уравнения для преобразователя запишем сначала его передаточную функцию:

Операторное уравнение, описывающее апериодическое звено 1-го порядка:

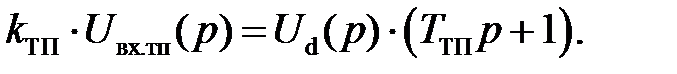
Дифференциальное уравнение для тиристорного преобразователя:

Входное напряжение преобразователя распишем через переменные и параметры системы, учитывая обратные связи по скорости и току, а также передаточные функции регуляторов:

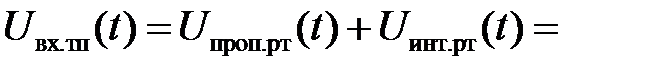
где 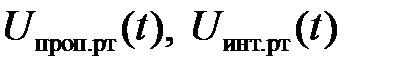– пропорциональная и интегральная составляющие выходного напряжения регулятора тока соответственно.

Для составления дифференциального уравнения для интегральной составляющей регулятора тока запишем сначала передаточную функцию регулятора в виде суммы составляющих:

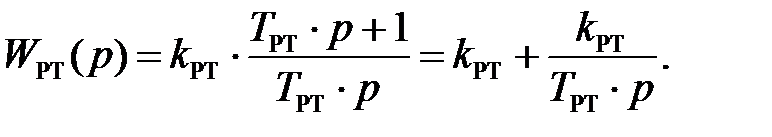
Уравнение для интегральной части регулятора тока выведем из ее передаточной функции:

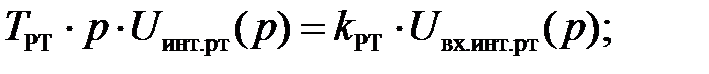
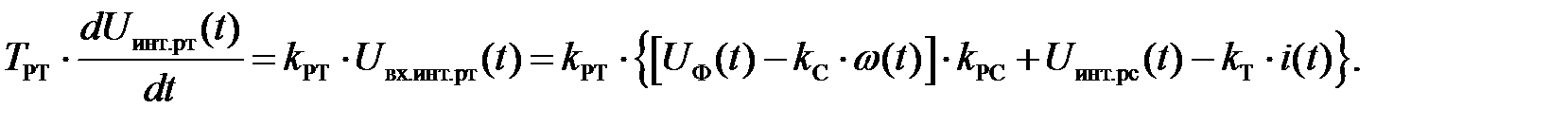
Аналогично составим уравнение для интегральной части регулятора скорости:

Передаточная функция апериодического фильтра на входе электропривода:

Уравнение состояния апериодического фильтра:

Сведем дифференциальные уравнения в систему:

Представим систему в нормальной форме Коши:

На рис. 54 изображена структурная схема двухконтурной системы управления ДПТ НВ с ПИ-регуляторами скорости и тока, а также апериодическим входным фильтром, собранная в MATLAB Simulink.

Рис. 54. Структурная схема двухконтурной системы управления ДПТ НВ с ПИ-регуляторами скорости и тока, а также апериодическим входным фильтром

На рис. 55 изображена корневая плоскость, полученная в MATLAB.

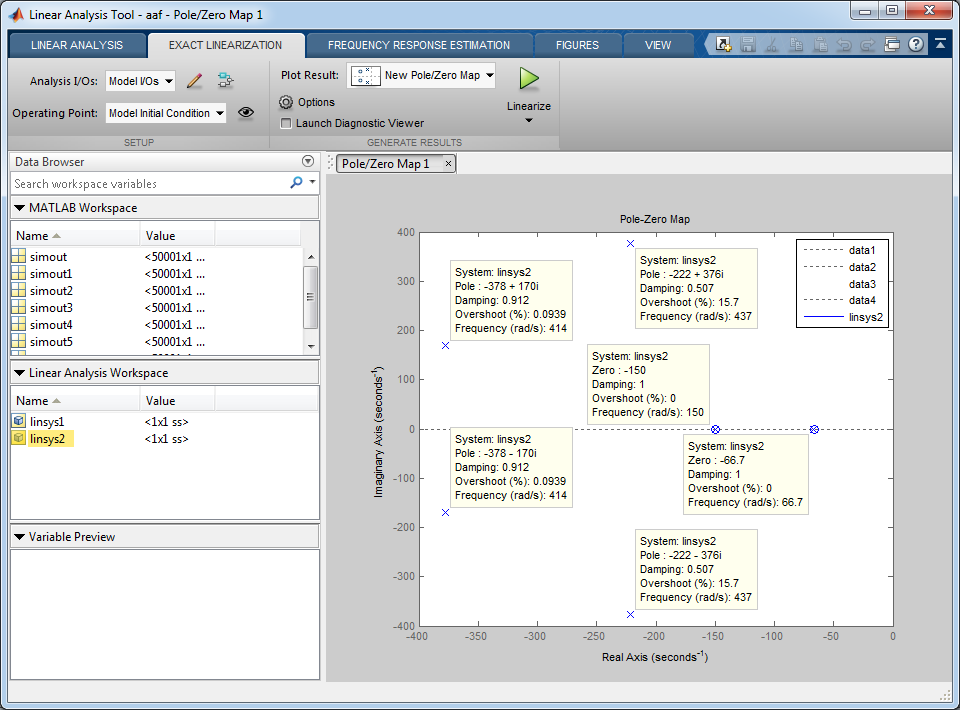
Рис. 55. Корневая плоскость

На рис. 56-60 изображены графики переходных процессов, полученных в MATLAB Simulink для скорости вала и тока якоря ДПТ, напряжений тиристорного преобразователя и интегральной части ПИ-регулятора тока, напряжения интегральной части ПИ-регулятора скорости и напряжения апериодического фильтра.

Рис. 56. Переходный процесс тока якоря ДПТ

Рис. 57. Переходный процесс скорости

Рис. 58. Переходный процесс напряжения интегральной части

ПИ-регулятора скорости

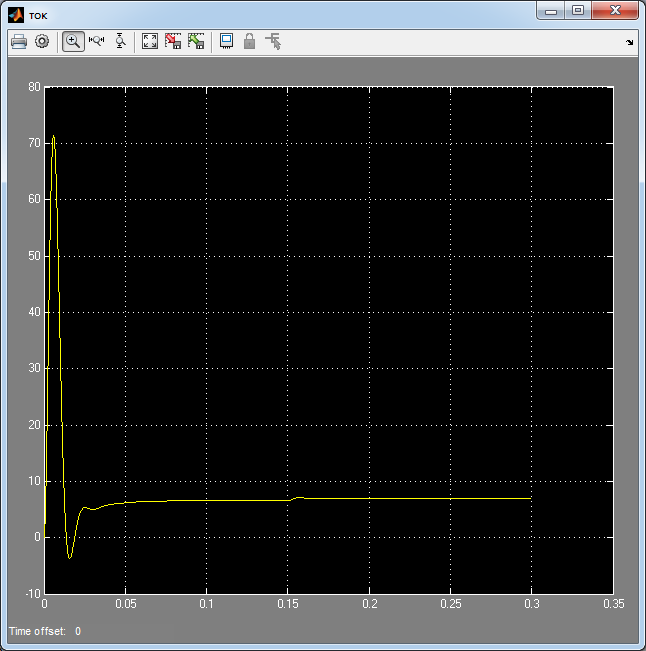
Рис. 59. Переходный процесс интегральной части ПИ-регулятора тока

Рис. 60. Переходный процесс напряжения тиристорного преобразователя

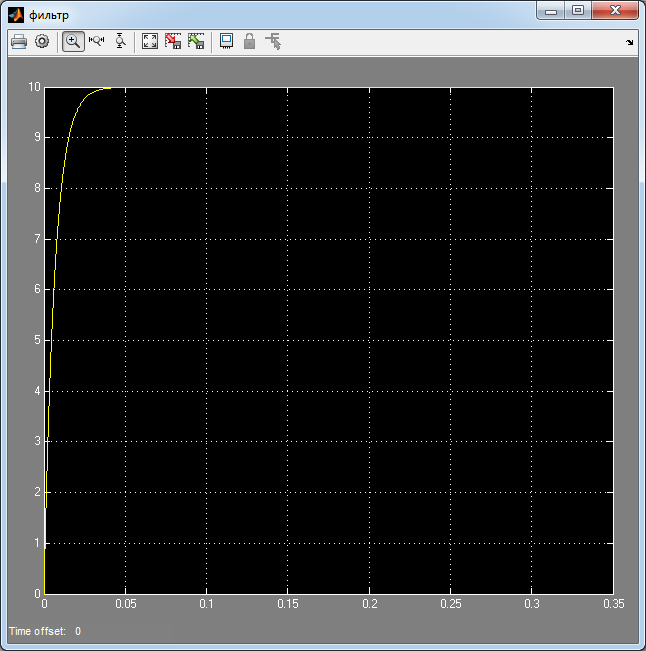
Рис. 61. Переходный процесс выходного напряжения апериодического фильтра на входе электропривода

Приведем решение СДУ в программной среде MathCAD операторным методом.

Присваиваем параметры:

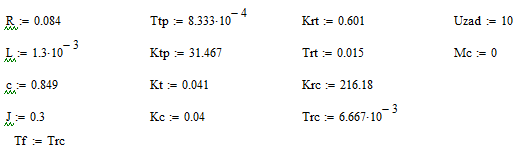
Матрицы параметров:

Находим собственные числа матрицы А:

Решение системы уравнений операторным методом:

На рис. 62-67 изображены графики переходных процессов, полученных в Mathcad для скорости вала и тока якоря ДПТ, напряжений тиристорного преобразователя и интегральной части ПИ-регулятора тока, напряжения интегральной части ПИ-регулятора скорости и напряжения апериодического фильтра.

Рис. 62. Переходный процесс для скорости вала

Рис. 63. Переходный процесс для тока якоря ДПТ

Рис. 64. Переходный процесс для напряжения тиристорного преобразователя

Рис. 65. Переходный процесс интегральной части ПИ-регулятора тока

Рис. 66. Переходный процесс напряжения интегральной части ПИ-регулятора скорости

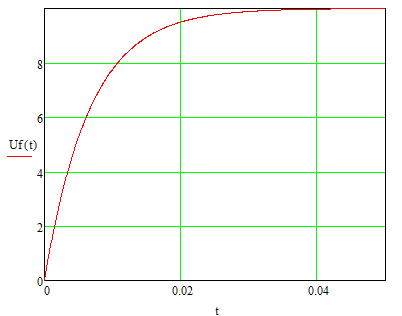
Рис. 67. Переходный процесс выходного напряжения апериодического фильтра на входе электропривода

Определим методом дихотомии время достижения максимума скорости электропривода, а также значение перерегулирования, и сравним с результатами в MATLAB Simulink.

Перерегулирование:

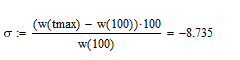
Время достижения первого максимума совпадает с MATLAB (рис. 68).

Рис. 68. Время достижения первого максимума

Вывод: в ходе лабораторной работы были получены графики переходных процессов в ДПТ для различных САУ: с П-регулятором скорости, с ПИ-регулятором скорости и с ПИ-регулятором скорости и входным апериодическим фильтром. Так же были построены переходные процессы для схем 5 порядка (схема с ПИ-регуляторами скорости и тока) и 6 порядка (с ПИ-регуляторами скорости и тока, а также с апериодическим фильтром на входе). Переходные процесс были получены в программе MATLAB для различных величин: тока, скорости, напряжения тиристорного преобразователя, интегральных частей ПИ-регуляторов скорости и тока, а также напряжения на апериодическом фильтре. Для проверки правильности получения переходных процессов они были сравнены с переходными процессами, полученными в программе Mathcad 2013. Собственные числа, полученные в MATLAB и Mathcad отличаются с небольшой погрешностью, следовательно, графики переходных процессов практически одинаковы. Наименьшим перерегулированием обладает система 6 порядка, так как на ее входе установлен фильтр. Так же в схемах с ПИ-регуляторами отсутствует статическая ошибка, например, при набросе нагрузки, в отличие от схем с П-регуляторами.

Дата добавления: 2015-10-29