Часть 3.1. Система 5 порядка

Структурная схема двухконтурной системы управления ДПТ НВ с ПИ-регуляторами скорости и тока приведена на рисунке 39.

Рис. 39. Структурная схема двухконтурной системы управления ДПТ НВ с ПИ-регуляторами скорости и тока приведена

САУ ДПТ с ПИ-регулятором скорости имеет пять переменных состояния (анализируя схему справа налево): скорость вала двигателя, ток якоря двигателя, выходное напряжение тиристорного преобразователя, представленного апериодическим звеном 1-го порядка, интегральная составляющая выходного напряжения ПИ-регулятора тока, а также интегральная составляющая выходного напряжения ПИ-регулятора скорости.

Соответственно, математическое описание электромеханической системы можно представить в виде системы из пяти дифференциальных уравнений первого порядка. Рассмотрим составление этих уравнений, начиная с выходной координаты электропривода и двигаясь последовательно к началу системы.

Динамику изменения скорости вала двигателя описывает дифференциальное уравнение движения:

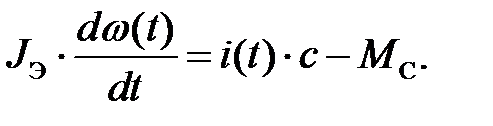
Уравнение равновесия напряжений для якорной цепи двигателя:

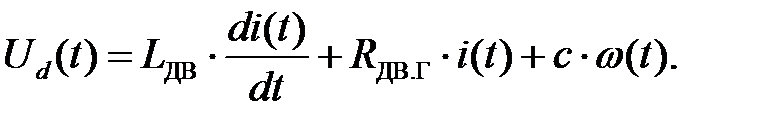
Для составления уравнения для преобразователя запишем сначала его передаточную функцию:

Операторное уравнение, описывающее апериодическое звено 1-го порядка:

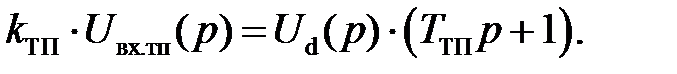
Дифференциальное уравнение для тиристорного преобразователя:

Входное напряжение преобразователя распишем через переменные и параметры системы, учитывая обратные связи по скорости и току, а также передаточные функции регуляторов:

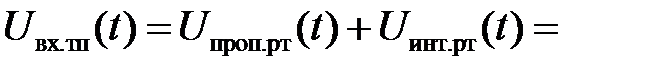
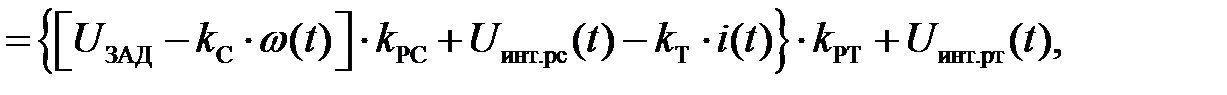
где 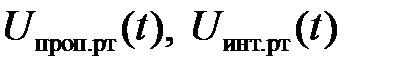– пропорциональная и интегральная составляющие выходного напряжения регулятора тока соответственно.

Для составления дифференциального уравнения для интегральной составляющей регулятора тока запишем сначала передаточную функцию регулятора в виде суммы составляющих:

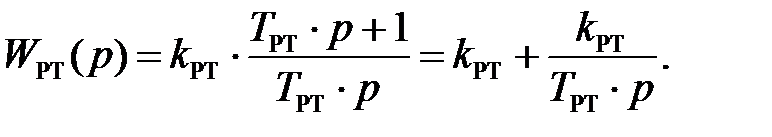
Уравнение для интегральной части регулятора тока выведем из ее передаточной функции:

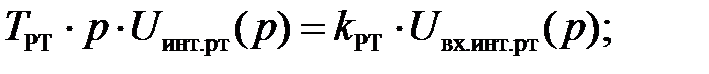
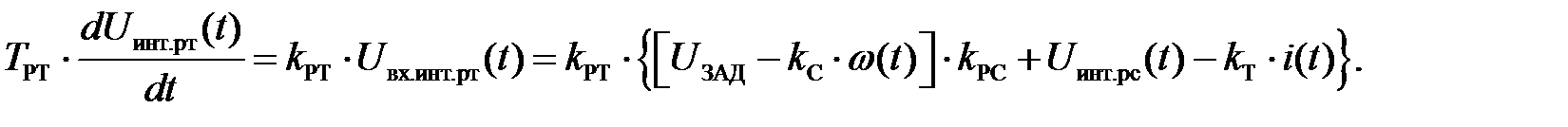
Аналогично составим уравнение для интегральной части регулятора скорости:

Сведем дифференциальные уравнения в систему:

Представим систему в нормальной форме Коши:

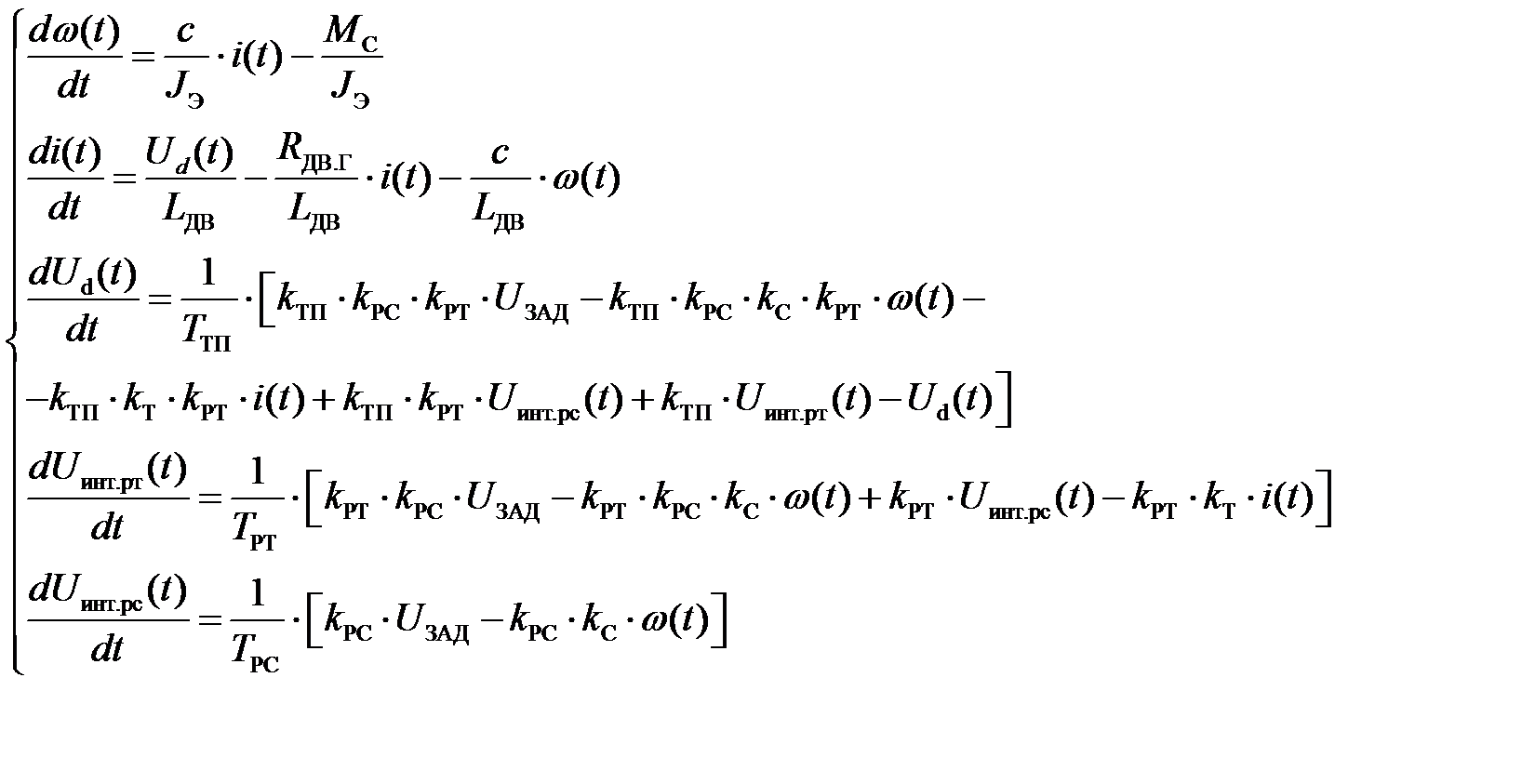
Приведем решение СДУ в программной среде MathCAD операторным методом.

На рис. 40 изображена имитационная модель САУ ДПТ с ПИ-регуляторами скорости и тока.

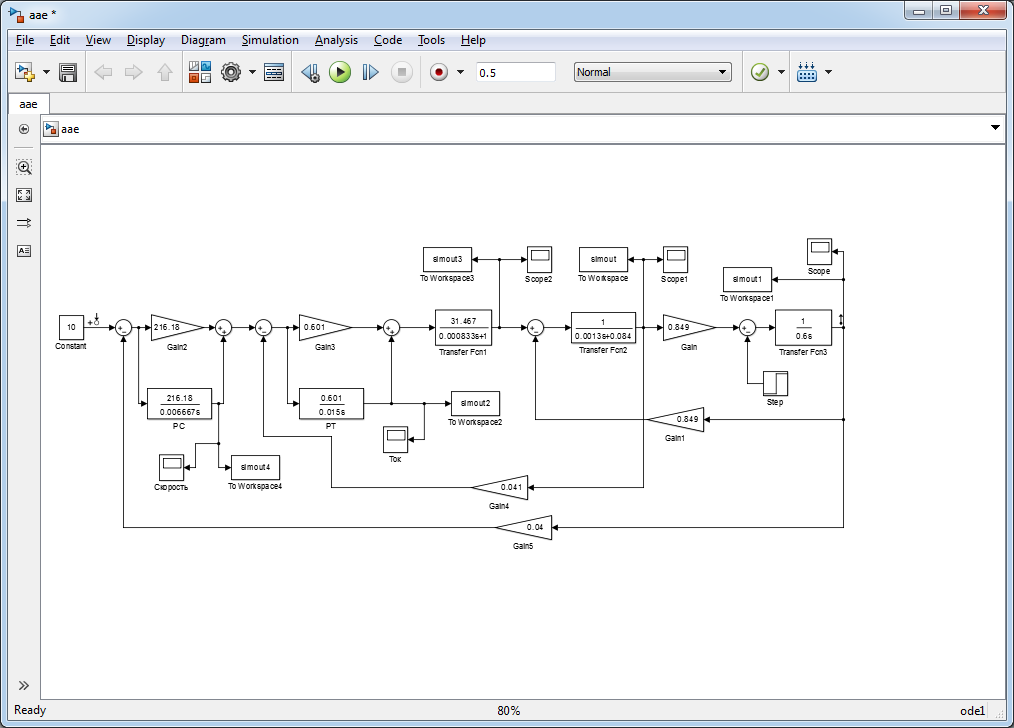
Рис. 40. Имитационная модель САУ ДПТ с ПИ-регуляторами скорости и тока

На рис. 41 изображена корневая плоскость, полученная в MATLAB.

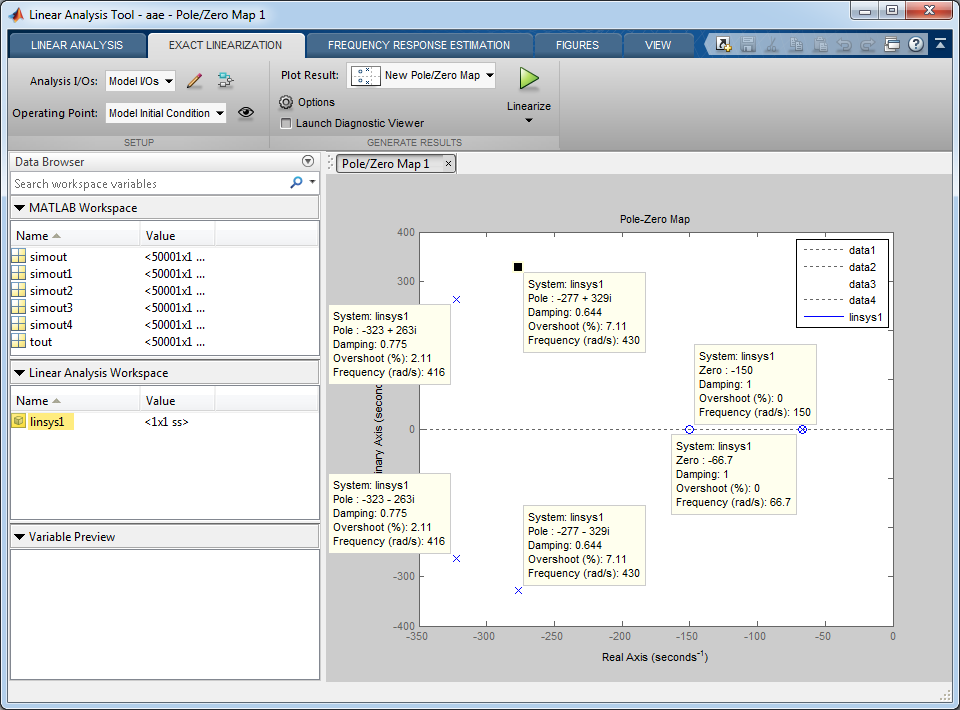
Рис. 41. Корневая плоскость

На рис. 42-46 изображены переходные процессы, полученные в MATLAB.

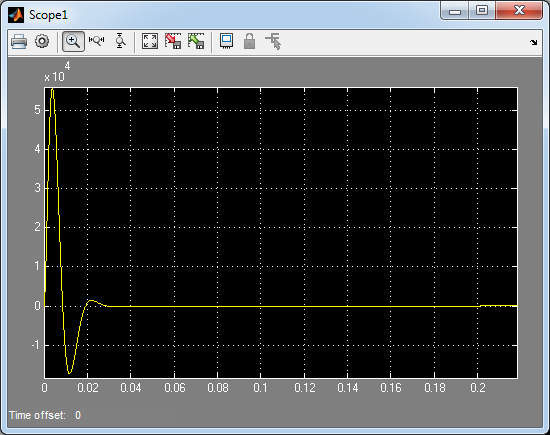
Рис. 42. Переходный процесс тока

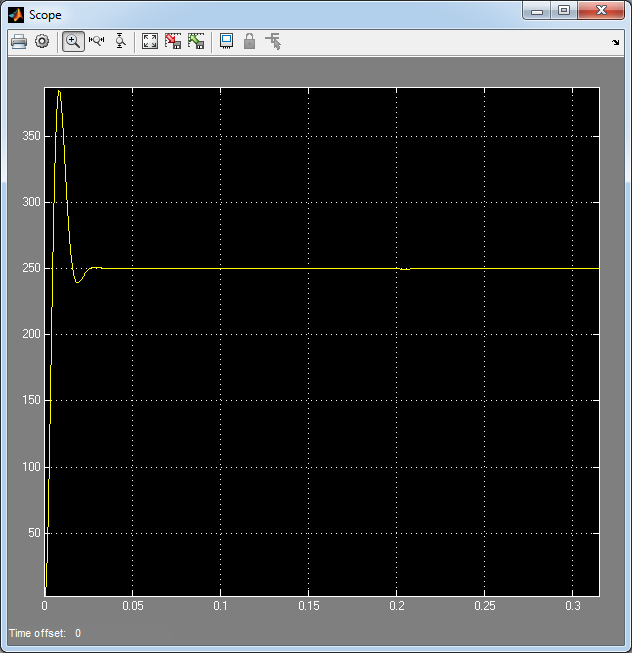
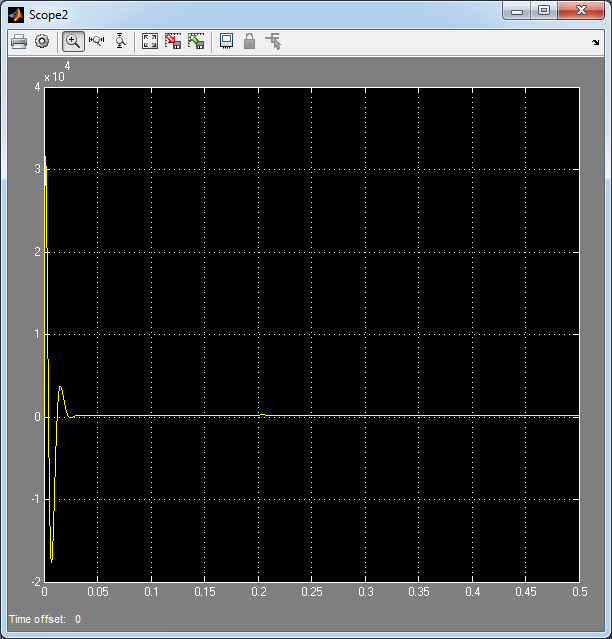Рис. 43. Переходный процесс скорости

Рис. 44. Переходные процессы напряжений тиристорного преобразователя

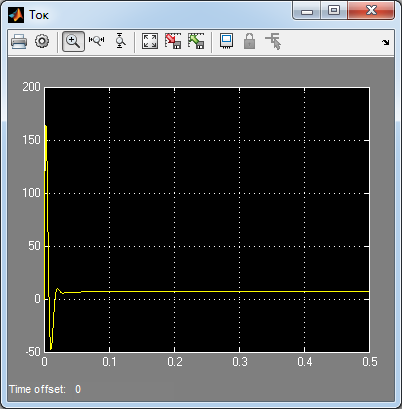
Рис. 45. Переходный процесс напряжения интегральной части ПИ-регулятора тока

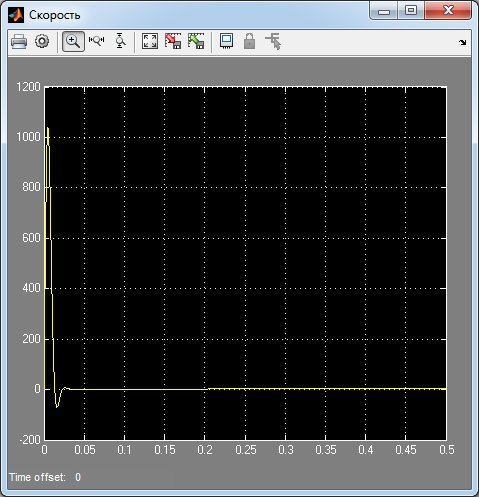
Рис. 46. Переходный процесс напряжения интегральной части

ПИ-регулятора скорости

Присваиваем параметры:

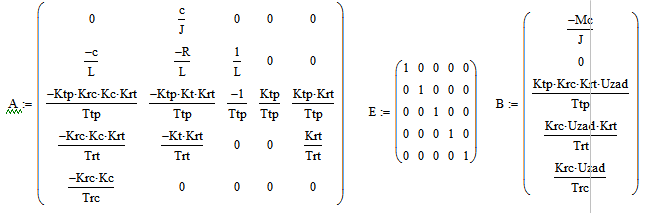
Матрицы параметров:

Находим собственные числа матрицы А:

Решение системы уравнений операторным методом:

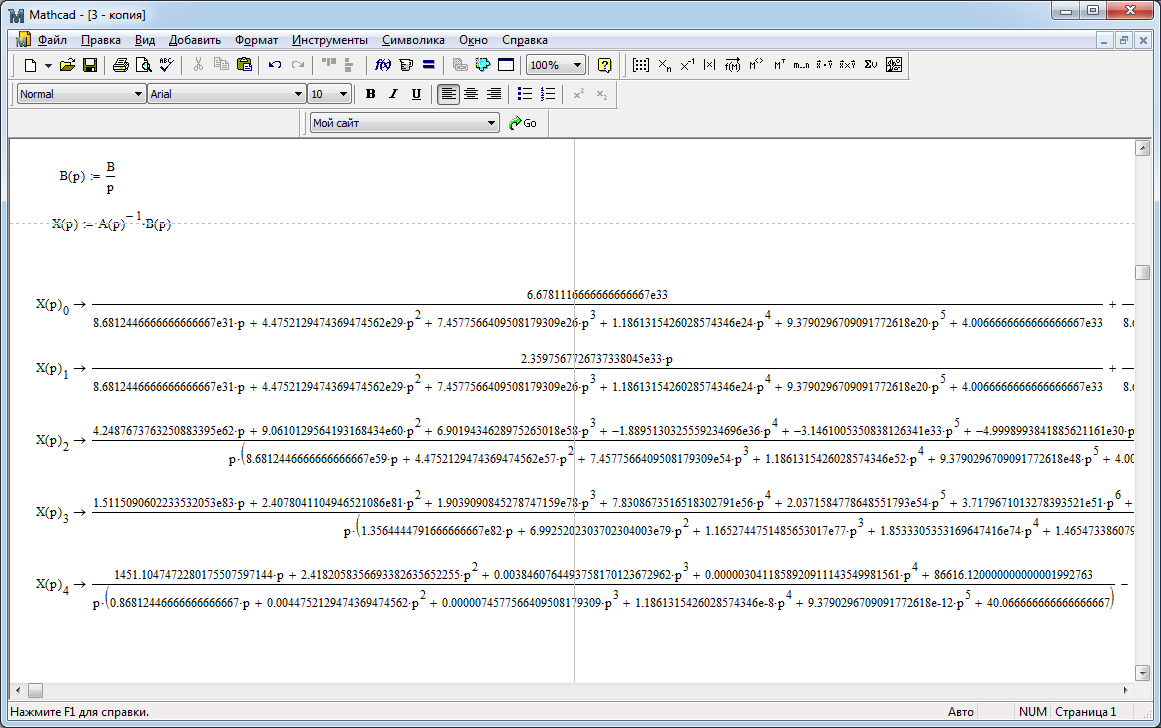
На рис. 47-51 изображены графики переходных процессов, полученных в Matchad для скорости вала и тока якоря ДПТ, напряжений тиристорного преобразователя и интегральной части ПИ-регулятора тока, напряжения интегральной части ПИ-регулятора скорости.

Рис. 47. Переходный процесс для скорости

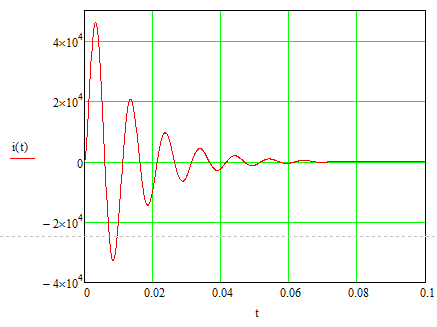
Рис. 48. Переходный процесс для тока

Рис. 49. Переходный процесс напряжений тиристорного преобразователя

Рис. 50. Переходный процесс интегральной части ПИ-регулятора тока

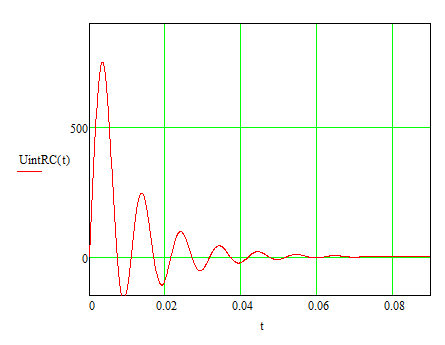
Рис. 51. Переходный процесс напряжения интегральной части

ПИ-регулятора скорости

Определим методом дихотомии время достижения максимума скорости электропривода, а также значение перерегулирования, и сравним с результатами в MATLAB Simulink.

Перерегулирование:

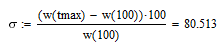
Дата добавления: 2015-10-29