Часть 2. Математическое моделирование замкнутой САУ ДПТ в программной среде MathCAD

Целью данной части работы является подтверждение адекватности имитационного моделирования в MATLAB работы двухконтурной САУ ДПТ путем численного и аналитического решения системы дифференциальных уравнений, описывающих замкнутую систему управления.

Приведем пример математического моделирования двухконтурной системы управления ДПТ НВ с П-регулятором скорости и ПИ-регулятором тока. Структурная схема данной системы приведена на рис. 28.

Рис. 28. Двухконтурная система управления ДПТ НВ с П-регулятором скорости и ПИ-регулятором тока

САУ ДПТ с П-регулятором скорости имеет четыре переменные состояния: скорость вала двигателя, ток якоря двигателя, выходное напряжение тиристорного преобразователя, представленного апериодическим звеном 1-го порядка, а также интегральная составляющая выходного напряжения ПИ-регулятора тока.

Динамику изменения скорости вала двигателя описывает дифференциальное уравнение движения:

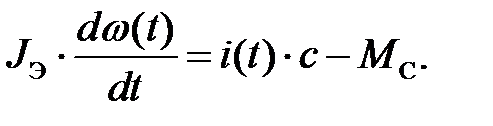
Уравнение равновесия напряжений для якорной цепи двигателя:

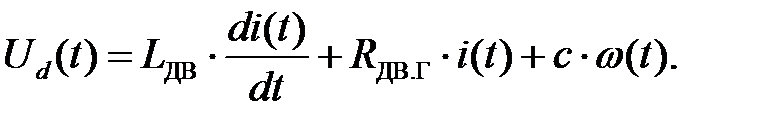
Для составления уравнения для преобразователя запишем сначала его передаточную функцию:

Операторное уравнение, описывающее апериодическое звено 1-го порядка:

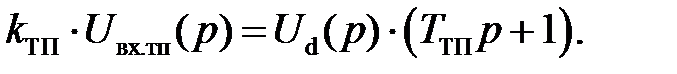
Дифференциальное уравнение для тиристорного преобразователя:

Входное напряжение преобразователя распишем через переменные и параметры системы, учитывая обратные связи по скорости и току, а также передаточные функции регуляторов:

где 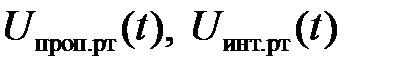– пропорциональная и интегральная составляющие выходного напряжения регулятора тока соответственно.

Для составления дифференциального уравнения для интегральной составляющей регулятора тока запишем сначала передаточную функцию регулятора в виде суммы составляющих:

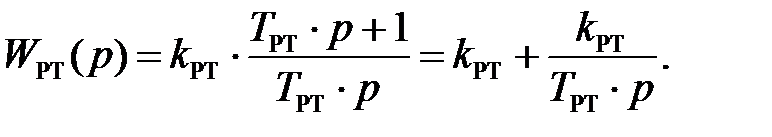
Уравнение для интегральной части регулятора выведем из ее передаточной функции:

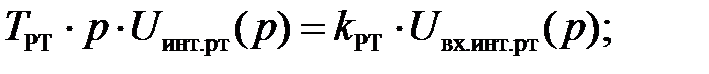
Сведем дифференциальные уравнения в систему:

Представим систему в нормальной форме Коши:

Имитационная модель САУ ДПТ с П-регулятором скорости и ПИ-регулятором тока изображена на рис. 29.

Рис. 29. Имитационная модель САУ ДПТ с П-регулятором скорости и ПИ-регулятором тока

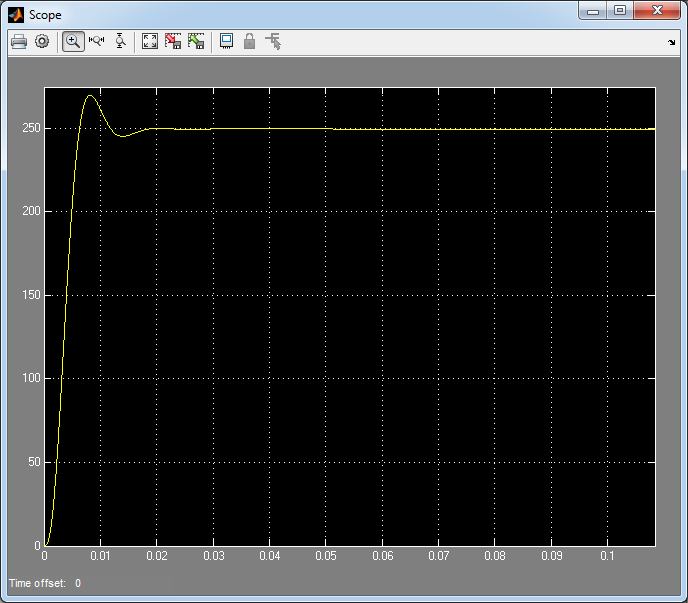
Рис. 30. Переходный процесс скорости

Рис. 31. Переходный процесс тока

Рис. 32. Переходный процесс интегральной части ПИ-регулятора тока

Рис. 33. Переходный процесс напряжения тиристорного преобразователя

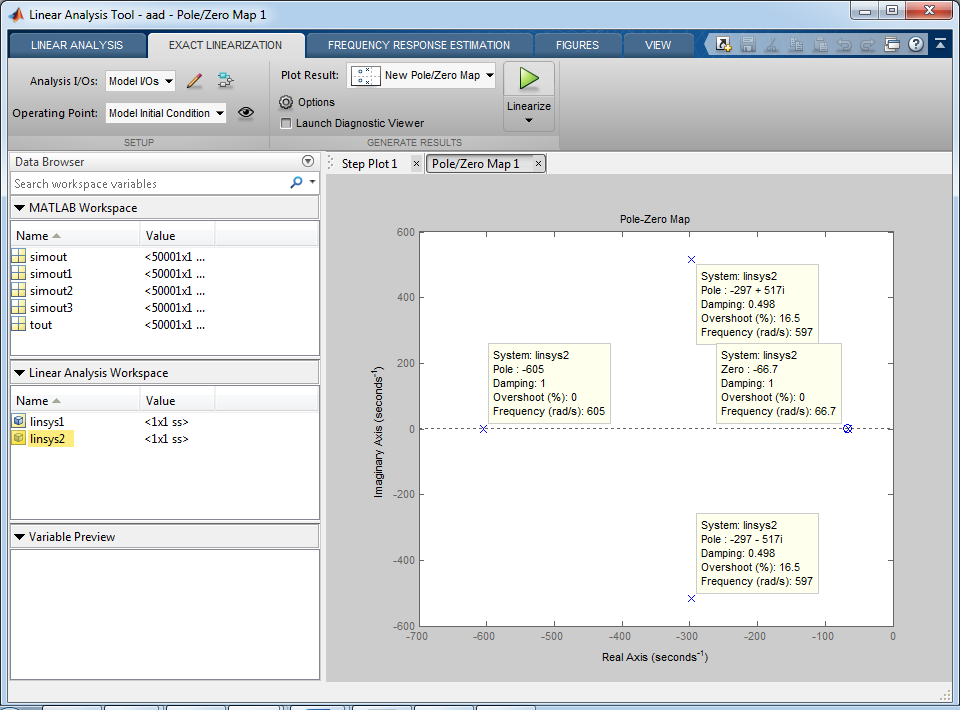
Рис. 34 – Корневая плоскость

Приведем решение СДУ в программной среде MathCAD операторным методом.

Присваиваем параметры:

Матрицы параметров:

Находим собственные числа матрицы А:

Полученные собственные числа сошлись с корневой плоскостью модели электропривода в MATLAB с небольшой погрешностью.

Операторный метод:

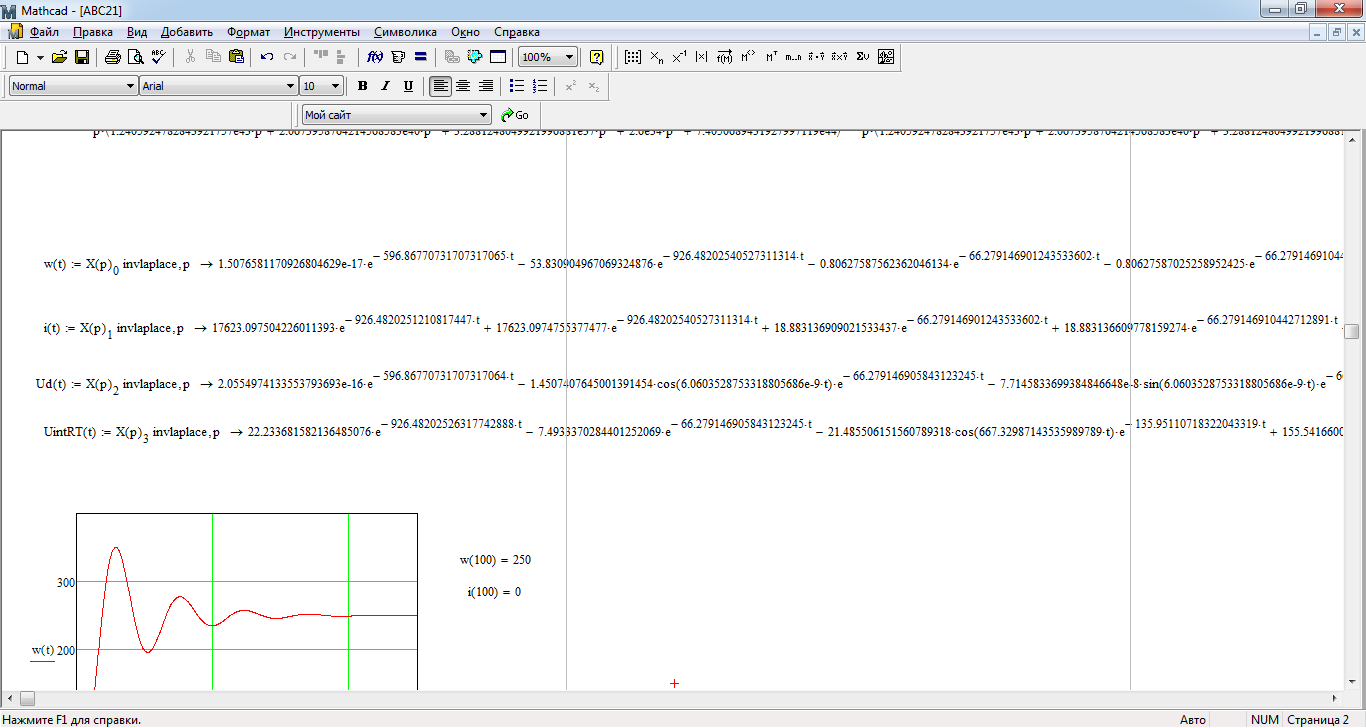
На рис. 35-38 изображены переходные процессы, полученные в Mathcad.

Рис. 35. Переходный процесс скорости

Рис. 36. Переходный процесс тока

Рис. 37. Переходный процесс напряжения тиристорного преобразователя

Рис. 38. Переходный процесс интегральной части ПИ-регулятора тока

Определим методом дихотомии время достижения максимума скорости электропривода, а также значение перерегулирования, и сравним с результатами в MATLAB Simulink.

Перерегулирование:

Дата добавления: 2015-10-29