Рівняння вигляду

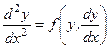(2.52)

не містить явним чином незалежної зміної .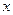

Зробивши підстановку

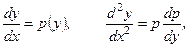(2.53)

одержимо рівняння першого порядку

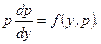
Інтегруючи його, знайдемо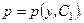

Підставивши це значення в (2.52), одержимо

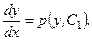
Після відокремлення змінних та інтегрування одержимо загальний інтеграл рівняння (2.53)

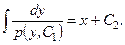
37.Лінійні однорідні диференціальні рівняння з постійними коефіцієнтами.

Диференціальне рівняння 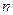- го порядку називається лінійним, якщо воно лінійне відносно шуканої функції 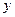та її похідних

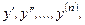тобто воно має такий вигляд

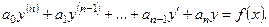(2.54)

Якщо 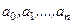- постійні, а 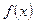- деяка неперервна на

проміжку 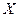функція, то рівняння (2.54) називається лінійним диференціальним рівнянням із сталими коефіцієнтами.

Якщо 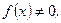то рівняння (2.54) називається лінійним неоднорідним диференціальним рівнянням (ЛНДР) із сталими коефіцієнтами. Якщо ж 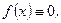то рівняння (2.54) має вигляд

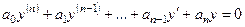(2.55)

і називається лінійним однорідним диференціальним рівнянням (ЛОДР) із сталими коефіцієнтами.

Загальний розв’язок ЛНДР (2.54) визначається як сума загального розв’язку 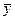ЛОДР (2.55) і якого-небудь частинного розв’язку 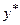ЛНДР (2.54), тобто

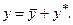(2.56)

Розглянемо ЛНДР із сталими коефіцієнтами другого порядку

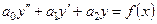(2.57)

і відповідне йому ЛОДР

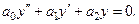(2.58)

Загальний розв’язок (2.57) визначається за формулою (2.56).

Для знаходження загального розв’язку ЛОДР (2.58) 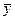складаємо характеристичне рівняння

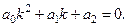(2.59)

Можливі такі випадки:

1. Корені характеристичного рівняння (2.59) дійсні та різні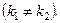

Тоді два лінійно незалежні розв’язки ЛОДР (2.58) 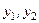мають

такий вигляд 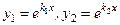і загальний розв’язок

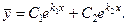(2.60)

2. Корені характеристичного рівняння (2.59) комплексні

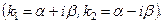Тоді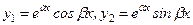

і

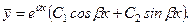(2.61)

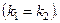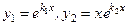3. Корені характеристичного рівняння (2.59) рівні Тоді

і

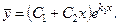(2.62)

Якщо 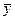- загальний розв’язок ЛОДР (2.58)

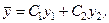
де 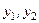- два лінійно незалежних розв’язки ЛОДР (2.58), то

частинний розв’язок ЛНДР (2.57) 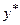шукається методом варіації

довільних сталих

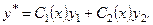(2.63)

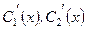знаходяться із системи рівнянь

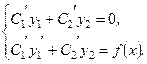(2.64)

Нехай 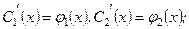тоді

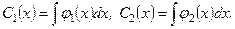
У випадку, коли права частина ЛНДР 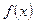спеціального

вигляду, частинний розв’язок ЛНДР можна шукати, не застосовуючи методу варіації довільних сталих.

1. Нехай права частина ЛНДР (2.57) має такий вигляд

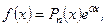(2.65)

де 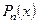- многочлен 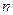- го степеня. Тоді частинний розв’язок ЛНДР

шукаємо у вигляді

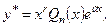(2.66)

де 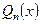- многочлен 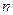- го степеня з невизначеними коефіцієнтами,

а 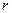- кратність числа 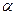, як кореня характеристичного рівняння (2.59)

(якщо 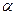не є коренем характеристичного рівняння (2.59), то ).

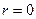2. Нехай права частина ЛНДР (2.57) має такий вигляд

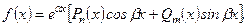(2.67)

Тоді

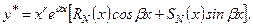(2.68)

де 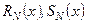- многочлени степеня 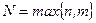з невизначеними коефіцієнтами, а 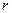- кратність числа ,

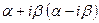як кореня характеристичного рівняння (2.59). Підставляючи (2.66) або (2.68) в рівняння (2.57), визначаємо коефіцієнти у многогчлена 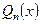або у многочленів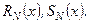

Дата добавления: 2015-10-29