Рівняння вигляду. Диференціальні рівняння з відокремлюючими змінними.

Диференціальні рівняння з відокремлюючими змінними.

Рівняння вигляду

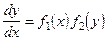, (2.32)

(2.33)

називаються рівняннями з відокремленими змінними. Їхні загальні

інтеграли будуть, відповідно

(2.34)

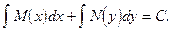(2.35)

Диференціальне рівняння

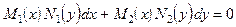(2.36)

називається рівнянням з відокремлюючими змінними. Воно зводиться

до рівняння (2.32) при діленні обох частин на вираз 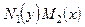(в

тій області, де і 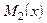не перетворюються в нуль).

35.Найпростіші типи диференціальних рівнянь першого порядку.

Однорідні рівняння першого порядку.

Рівняння першого порядку (2.31) називається однорідним, якщо - однорідна функція нульового виміру відносно і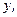

тобто при довільному

Однорідне рівняння зводиться до рівняння з відокремлюючими змінними з допомогою підстановки

(2.37)

Лінійні диференціальні рівняння першого порядку.

Лінійним рівнянням першого порядку називається рівняння, яке є лінійним відносно шуканої функції та її похідної. Воно має такий вигляд

(2.38)

де - задані неперервні функції від (або постійні).

Загальний розв’язок (2.38) шукається у вигляді добутку двох

функцій від :

, (2.39)

де обчислюються за формулами

(2.40)

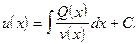(2.41)

Рівняння Бернуллі.

Рівняння

(2.42)

де - неперервні функції від (або постійні), а

називається рівнянням Бернуллі.

Поділивши рівняння (2.42) на і зробивши підстановку

(2.43)

одержимо лінійне рівняння.

Рівняння в повних диференціалах.

Рівняння

(2.44)

називається рівнянням в повних диференціалах, якщо

- неперервні диференційовні функції, для яких виконується умова

(2.45)

причому частинні похідні - неперервні в деякій області.

Загальний інтеграл рівняння (2.46) має такий вигляд

. (2.46)

36.Способи пониження порядку в диференціальних рівняннях.

1. Рівняння вигляду (2.47)

Зробивши заміну (2.48)

це рівняння зводиться до диференціального рівняння першого порядку , інтегруючи яке одержимо

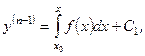
тобто рівняння

(2.49)

Аналогічно понижуємо порядок одержаного диференціального рівняння.

Рівняння вигляду

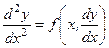(2.50)

не містить явним чином шуканої функції .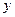

З допомогою підстановки

(2.51)

рівняння зводиться до диференціального рівняння першого порядку.

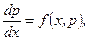
проінтегрувавши яке, одержимо

Тоді загальний інтеграл рівняння (2.50) буде мати такий вигляд

Аналогічно можна проінтегрувати і рівняння

поклавши

Дата добавления: 2015-10-29