Методические указания. Для выполнения п.п

Для выполнения п.п. 2, 5-7 Программы работы рекомендуется воспользоваться методом стандартных коэффициентов нахождения эталонного оператора замкнутой системы. Вид переходного процесса определяется значениями нулей и полюсов передаточной функции. Оптимальное с некоторой точки зрение расположение нулей и полюсов на комплексной плоскости обеспечит желаемый вид переходной характеристики. Оптимальные расположения нулей и полюсов определяются соответствующими значениями коэффициентов полиномов числителя и знаменателя передаточной функции. Такие значения называют стандартными.

При исследовании схемы с П-регулятором в качестве типовой функции можно взять передаточную функцию замкнутой системы, не содержащую нулей:

.

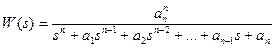Для такой системы переходный процесс будет оптимальным с точки зрения быстродействия и отсутствия перерегулирования, если корни знаменателя будут вещественными и кратными, т.е. характеристический полином будет иметь вид H (s)=(s + q) ⁿ, где q определяет быстродействие системы. Задавшись значением q, можно определить коэффициенты передаточной функции.

Если передаточная функция имеет один нуль

,

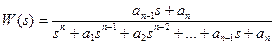то чтобы уменьшить выброс, вызванный влиянием нуля, надо «разводить» корни полинома знаменателя по действительной оси. Корни рекомендуется располагать на отрицательной вещественной полуоси по арифметической прогрессии. Значения коэффициентов полинома знаменателя для такого расположения корней приведены в табл. 2.

Таблица 2

Значения коэффициентов полинома знаменателя

для передаточной функции с одним нулем

n	1-й член прогрессии	Разность прогрессии	Коэффициенты знаменателя
	0,5	1,5	a 0=1 a 1=2,5 q; a 2= q ^2
	0,138	1,81	a 0=1; a 1=5,84 q; a 2=8,11 q ^2; a 3= q ^3

Если передаточная функция имеет два нуля

,

то корни рекомендуется располагать на отрицательной вещественной полуоси по геометрической прогрессии. Значения коэффициентов полинома знаменателя для такого расположения корней приведены в табл. 3.

Таблица 3

Значения коэффициентов полинома знаменателя

для передаточной функции с двумя нулями

n	1-й член прогрессии	Знаменатель прогрессии	Коэффициенты знаменателя
	0,182	5,5	a 0=1; a 1=6,7 q; a 2=6,7 q ^2; a 3= q ^3

Далее осуществляется приближение оператора реальной системы к эталонному.

Передаточная функция устройства, собранного на базе операционного усилителя, включенного по инвертирующей схеме, определяется по формуле:

,

где z_вх (s) – входное сопротивление, z_ос (s) – сопротивление обратной связи.

Содержание отчета

1. Принципиальные схемы САР с различными регуляторами.

2. Передаточные функции регуляторов.

3. Расчет параметров регуляторов.

4. Временные характеристики регуляторов.

5. Графики переходных процессов при действии различных регуляторов. Значения показателей качества.

6. Графики ЛАЧХ и ЛФЧХ при действии различных регуляторов. Значения частоты среза и запасов устойчивости по амплитуде и фазе.

7. Вывод о характере влияния пропорциональной, дифференцирующей и интегрирующей составляющих на показатели качества и запасы устойчивости.

Контрольные вопросы

1. Какие методы оптимизации известны?

2. Какие свойства САР приобретает при введении интегрирующей составляющей в корректирующее устройство?

3. Какие свойства САР приобретает при введении дифференцирующей составляющей в корректирующее устройство?

4. В каких случаях целесообразно применять ПИД-регуляторы?

5. Какими недостатками обладает САР с ПИД-регулятором?

Дата добавления: 2015-10-29