Методические указания. 1. Для выполнения п

1. Для выполнения п. 1 «Программы работы» записать линеаризованное характеристическое уравнение (значение коэффициента гармонической линеаризации взять из таблицы). Выделив в нем действительную и мнимую часть, приравнять их нулю. Получить формулу, связывающую амплитуду периодического решения с параметрами системы.

2. Для исследования устойчивости периодического решения использовать приближенный критерий, согласно которому должно выполняться неравенство

,

где а и w – амплитуда и частота соответственно вблизи периодического решения, а звездочка означает, что после взятия производных необходимо подставить значения амплитуды и частоты для периодического решения а = А и w = W.

Для определения производных рекомендуется воспользоваться редактором MathCAD.

3. Для выполнения п.п. 2 «Программы работы» воспользоваться редактором MathCAD.

4. При выполнении п. 3 «Программы работы», воспользовавшись редактором MathCAD, построить АФХ линейной части, взятую с обратным знаком, и кривую гармонического коэффициента. Определить значения частоты и амплитуды автоколебаний в точке их пересечения.

Таблица 1

Типовые нелинейности и выражения

для коэффициентов гармонической линеаризации

№	Типовая нелинейность	Коэффициент гармонической линеаризации
	Идеальная релейная
	Сухое трение
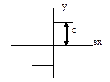
	С насыщением	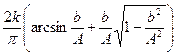при A³b
	Релейная с зоной нечувствительности	при A³b
	С зоной нечувствительности и насыщением	при A³b2

Таблица 2

Исходные данные

№ варианта	Передаточная функция линейной части системы	Значения параметров	Изменяе-мый параметр	Типовая нелинейность
		Ky=10; T1=0.1; T2=0.002 b=1; k=2	ky
		Ky=20; T1=0.05; T2=0.001 c=10	T1
		Ky=2; T1=0.1; T2=0.005 b1=1; b2=2; k=2	T2
		Ky=10; T1=0.5; T2=0.02 c=5	Ky
		Ky=10; T1=0.1; T2=0.002 c=2	T
		Ky=20; T1=0.2; T2=0.002 c=5	T1
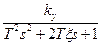
		Ky=10; T=0.1; x=0.2 b=1; k=2	ky
		Ky=10; T1=0.1; T2=0.002 c=1	T
		Ky=10; T1=0.5 b1=1; b2=1.5; k=2	ky

Содержание отчета

1. Структурная схема САР.

2. Описание используемых методов при определении амплитуды и частоты автоколебаний.

3. Графики зависимости амплитуды и частоты автоколебаний от указанного параметра.

4. Графики АФХ.

5. Вывод по работе.

Контрольные вопросы

1. В чем суть метода гармонической линеаризации?

2. В чем суть метода Л.С.Гольдфарба?

3. Каким образом можно замоделировать указанную типовую нелинейность?

4. Вывести значение коэффициента гармонической линеаризации.

Дата добавления: 2015-10-29