Построение точек на поверхности конуса

Если на поверхности конуса задана одна проекция точки А (например, фронтальная проекция на рисунке 140), то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности конуса и проведенной через точку А, или окружности, расположенной в плоскости, параллельной основанию конуса.

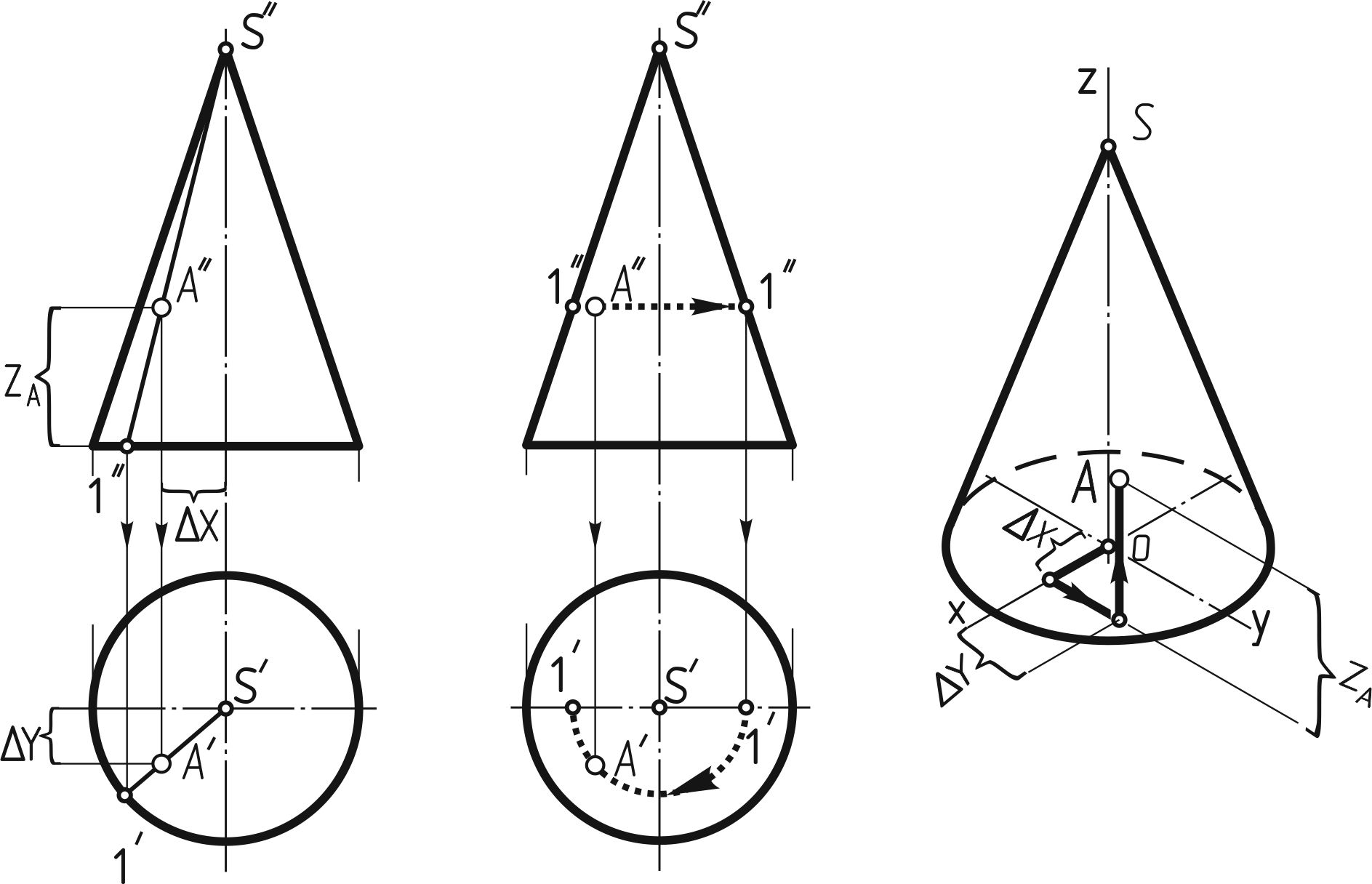
а б в

Рисунок 140

В первом случае (рисунок 140, а) через точку A проводят фронтальную проекцию 1''S'' вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки 1, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию 1' этой образующей, на которой при помощи линии связи, проходящей через A', находят искомую точку A.

Во втором случае (рисунок 140, б) вспомогательной линией, проходящей через точку А, будет окружность, расположенная на конической поверхности и параллельная плоскости Н - параллель. Фронтальная проекция этой окружности изображается в виде отрезка 1''1'' горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция A' точки А находится на пересечении линии связи, опущенной из точки A', с горизонтальной проекцией вспомогательной окружности.

Если заданная фронтальная проекция 1'' точки 1 расположена на контурной (очерковой) образующей, то горизонтальная проекция точки находится без вспомогательных линий.

В изометрической проекции точку А, находящуюся на поверхности конуса, строят по трем координатам (см. рисунок 140, в): DX, DY и Z_А. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата DX; из конца ее параллельно оси у проведена прямая, на которой отложена координата DY; из конца отрезка, параллельно оси z проведена прямая, на которой отложена координата Z_А. В результате построений получим искомую точку А.

Шар. Шаром (рисунок 141) называют тело, полученное при вращении полукруга ABC (образующая) вокруг его диаметра АС (ось вращения), а поверхность, которую при этом описывает дуга ABC, называется шаровой или сферической. Шар относится к телам, ограниченным только поверхностью вращения.

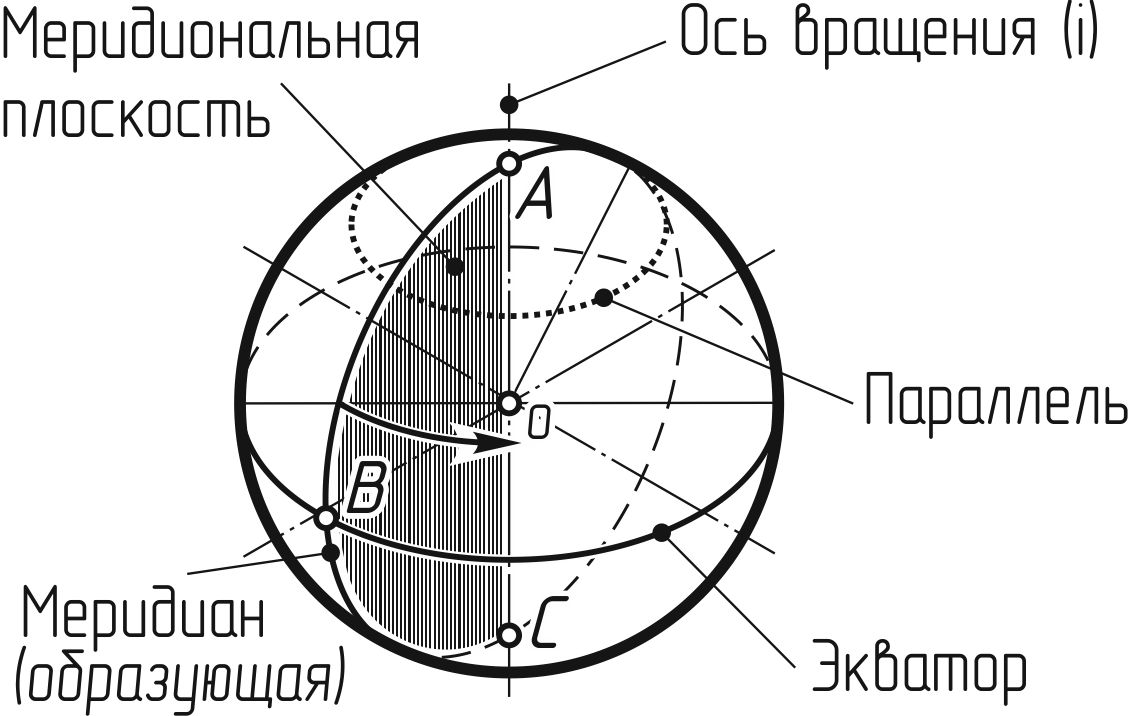
Рисунок 141

Шаровая (сферическая) поверхность является геометрическим местом точек, равноудаленных от одной точки О, называемой центром шара. Если шар рассечь горизонтальными плоскостями, то в сечении получатся окружности – параллели. Наибольшая из параллелей имеет диаметр равный диаметру шара. Такая окружность называется экватором. Окружности же, получаемые в результате сечений шара плоскостями, проходящими через его ось вращения, называются меридианами.

Дата добавления: 2015-10-28