Построение точки на поверхности пирамиды

Пример.

Пусть, например, дана фронтальная проекция А'' точки А, расположенной на грани пирамиды 1S2, и требуется найти другую проекцию этой точки.

Первый способ. Для решения этой задачи проведем через A'' вспомогательную прямую любого направления и продолжим ее до пересечения с фронтальными проекциями 1''S'' и 2''S'' ребер в точках N'' и M''. Затем проведем из точек N'' и M'' линии связи до пересечения с горизонтальными проекциями 1'S' и 2'S' этих ребер. Соединив точки, получим горизонтальную проекцию вспомогательной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию A' точки А. Профильную проекцию этой точки находят по линиям связи.

Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на 133, а. Дана треугольная пирамида. Через заданную фронтальную проекцию A'' точки А проводят вспомогательную прямую, проходящую через вершину пирамиды и расположенную на ее грани точку ребра основания F,. Горизонтальную проекцию F'S' вспомогательной прямой находят, применяя линию связи. Искомая горизонтальная проекция А' точки А находится на пересечении линии связи, проведенной из точки A'', с горизонтальной проекцией F'S' вспомогательной прямой.

Если необходимо определить положение точки на ребре, совпадающем с линий связи, без третей проекции, проводят вспомогательную прямую через точку параллельно соответствующему отрезку основания (рисунок 133 б). Определение положения точки В на горизонтальной плоскости проекций, лежащей на ребре S2, начинается с проведения через фронтальную проекцию В'' точки В линии параллельной линии основания 23 до пересечения с ребром пирамиды S3. Строим горизонтальную проекцию точки пересечения вспомогательной линии и ребра S3 точку С,опуская линию связи на горизонтальную проекцию ребра S'3'. Из точки С' параллельно линии 1'3' провидим горизонтальную проекцию вспомогательной линии до пересечения с линией связи от фронтальной проекции А'' точки А.

Аксонометрическая проекция пирамиды выполняется следующим образом (рисунок 133, б).

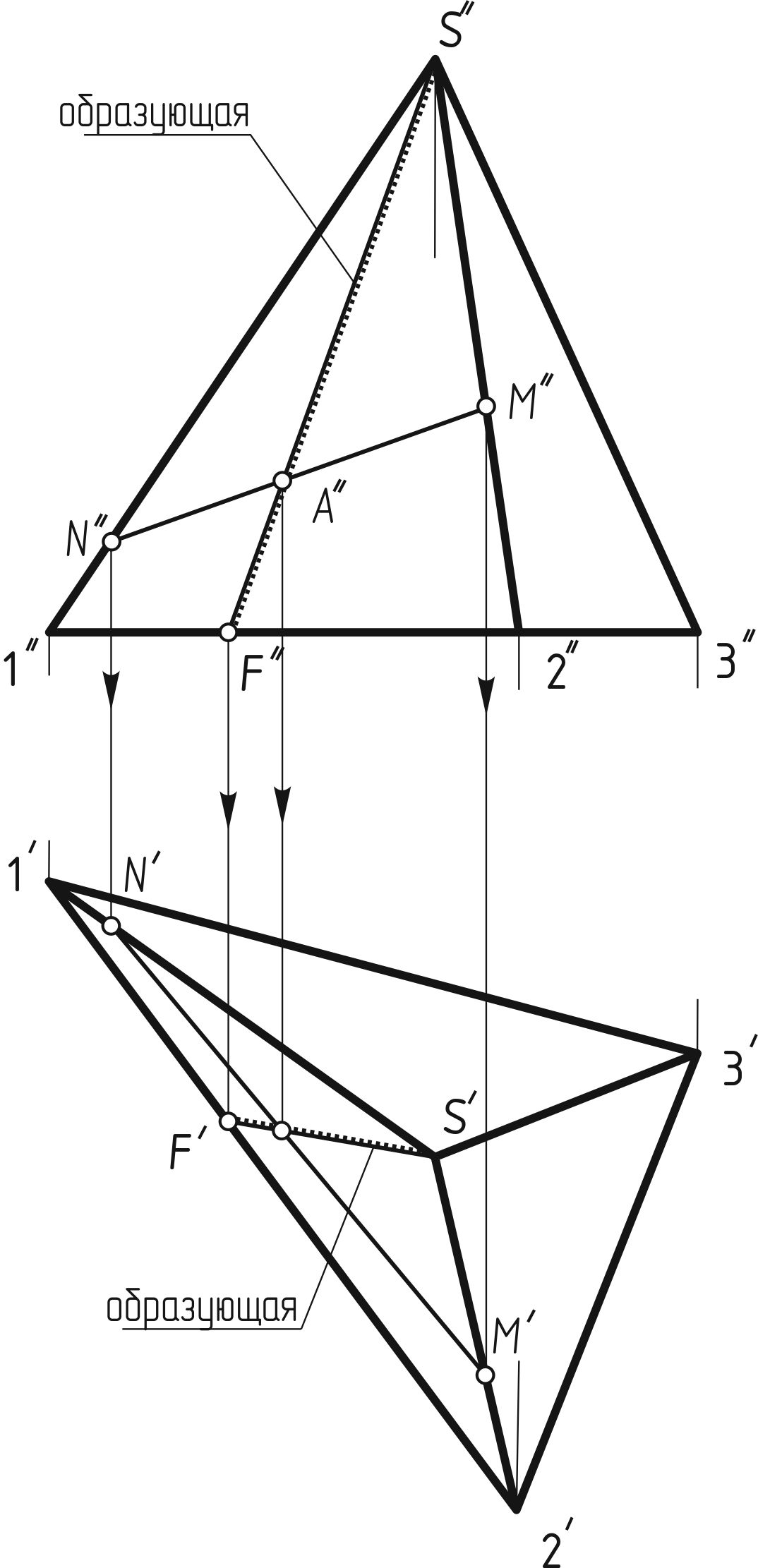
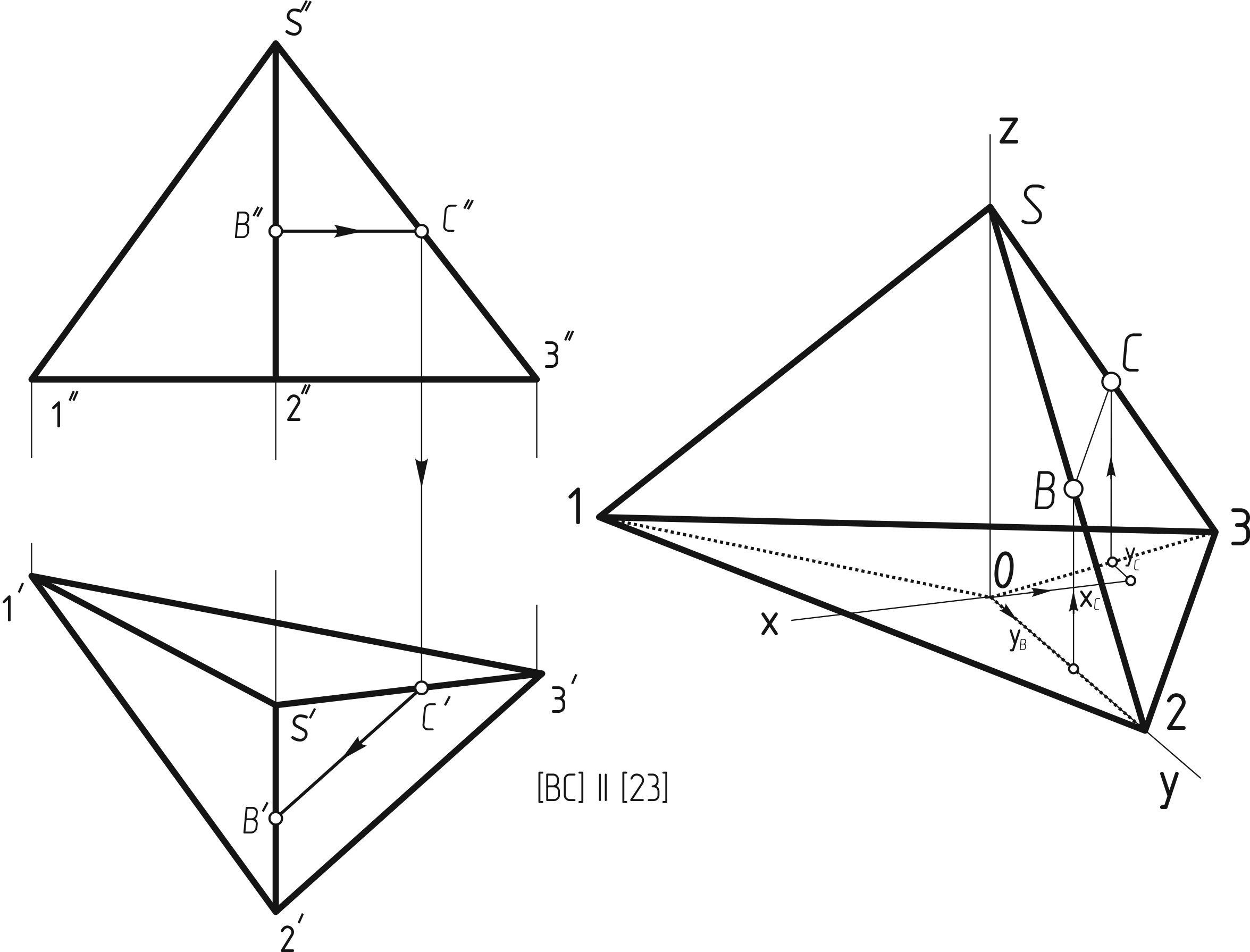
а б

Рисунок 133

Вначале строят основание, для чего каждую вершину основания строят по координатам, откладывая их вдоль оси OY и OX соответственно. Из точки О проводят ось z и на ней откладывают высоту пирамиды. Вершину S соединяют с вершинами основания прямыми линиями — ребрами.

Аксонометрическую проекцию точки С, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От начала координат О по оси х откладывают координату X_С, из ее конца параллельно оси у — половину координаты Y_С и из конца этой координаты параллельно оси z — третью координату Z_С. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х откладывают координату X_B и из конца се проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.

---

Дата добавления: 2015-10-28