Коробовые кривые

Коробовой кривой называется односторонне выпуклая циркульная кривая (замкнутая или незамкнутая), образуемая сопряжением дуг: окружностей. Существует несколько разновидностей коробовых кривых.

Овал – замкнутая коробовая кривая, имеющая две оси симметрии. Элементами, определяющими размер овала, являются его длина и ширина, измеряемые по осям симметрии.

Построение овала по его длине AB и ширине CD показано на рисун-ке 59. Вначале проводят две взаимно перпендикулярные прямые, пересекающиеся в точке О (рисунок 59, а). На горизонтальной прямой в обе стороны от точки О откладывают отрезок , а на вертикальной – . Точки A и С соединяют прямой линией, и из точки О описывают дугу радиусом OA до пересечения ее с прямой CD в точке E. На прямой AC откладывают отрезок CF=CE и получают точку F. Через середину отрезка AF проводят перпендикуляр и на пересечении его с прямыми AB и CD получают точки O₁ и O₂. На прямых AB и CD строят точки O₃ и O₄, симметричные точкам O₁ и O₂ относительно центра О (рисунок 59 б). Точки O₁, O_2,O₃, O₄ являются центрами сопрягаемых дуг, определяющих контур овала, а точки касания дуг располагаются на прямых O₁O₂, O₃O₂, O₁O₄ и O₃O₄. Из центров O₁ и O₃ описывают дуги радиусом R₁ = O₁A, а из центров O₂ и O₄ – дуги радиусом R₂ = O₂C и получают контур овала.

а б

Рисунок 59

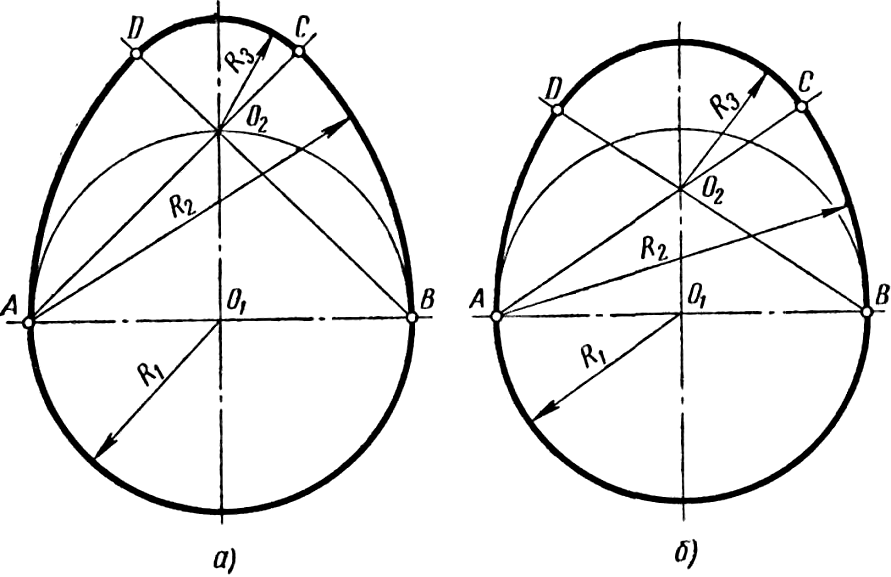
Овоид – замкнутая коробовая кривая, имеющая одну ось симметрии. Построение овоида по его ширине – отрезку AB приведено на рисунке 60, а. Через середину отрезка AB – точку O₁ проводят прямую, перпендикулярную к нему. Из точки O₁ описывают окружность радиусом и на пересечении ее с перпендикуляром получают точку O₂. Далее проводят прямые AO₂ и BO₂ и продолжают их за точку O₂. Из точек A и В радиусом R₂ = AB описывают две дуги до пересечения их в точках C и D с проведенными прямыми. Последнюю дугу радиусом R₃ = O₂C описывают из точки O₂.

Если точку O₂ расположить ближе к точке O₁ или дальше от нее, то овоид получится соответственно более тупым или более острым. Для построения тупого овоида задают его ширину AB и расстояние между центрами O₁O₂ (рисунок 60 б). Порядок построения остается прежним.

а б

Рисунок 60

Коробовые кривые сводов относятся к незамкнутым коробовым кривым. Они находят применение при строительстве сводов и арок мостов, входов в здания, различных перекрытий, например метро и т. п. Ниже разобрано построение коробовых кривых пологого, крутого и ползучего сводов.

Построение коробовой кривой пологого свода по его ширинеАВи высотеОС (рисунок 61). На горизонтальной прямой откладывают ширину свода – отрезок AB и через его середину точку О проводят прямую, перпендикулярную к нему. На этой прямой от точки О откладывают высоту свода – отрезок OC. Из точки О радиусом OA описывают дугу AE и на ней отмечают точку D с помощью того же радиуса OA, но с центром в точке А. Точку D соединяют прямыми с точками А, Е и О. Затем через точку С проводят прямую CF || DE до пересечения ее с прямой AD в точке F. Через точку F проводят прямую FO₂ || DO до пересечения ее с отрезком AB в точке O₁, а с прямой OC в точке O₂. Точку O₃ получают при помощи дуги радиусом OO₁. Полученные точки O₁, O₂ и O₃ являются центрами дуг, из которых состоит данная кривая. Радиусом R₁ = O₃B описывают дуги из центров O₁ и O₃, а радиусом R₂ = O₂C – дугу из центра O₂.

Рисунок 61

Построение коробовой кривой крутого свода по ширине AB и высоте ОС (рисунок 62). Отрезок AB делят пополам, строят прямоугольник АЕСО и проводят в нем диагональ AC. Углы EAC и ECA делят пополам. На пересечении биссектрис этих углов получают точку D и из нее опускают перпендикуляр на диагональ AC. Перпендикуляр продолжают до пересечения с отрезками: OC в точке O₁ и AB в точке O₂. Точку O₃ получают при помощи дуги радиусом OO₂. Точки O₁, O₂ и O₃ являются центрами дуг радиусами R₁ и R₂, с помощью которых строят контур кривой.

Рисунок 62

Построение коробовой кривой ползучего свода по его ширине АВ и прямой CD, касательной к вершине свода (рисунок 63). Строят отрезок AB, представляющий ширину свода, и прямую CD (ее называют замковой прямой). Из точек A и В восставляют к отрезку AB перпендикуляры и продолжают их до пересечения с прямой CD в точках М и N. На прямой CD откладывают отрезок EM = AM. Из полученной точки Е – вершины свода восставляют перпендикуляр к прямой CD и на пересечении его с отрезком AB отмечают точку O₁. На прямой BN откладывают от точки N отрезок FN=EN. Из точки F проводят прямую, параллельную отрезку AB, до пересечения с прямой EO₁ в точке O₂. В точках O₁ и O₂ находятся центры дуг R₁ = O₁A и R₂ = O₂F, определяющих контур ползучего свода.

Рисунок 63

Дата добавления: 2015-10-28