Повертаємось до практичних дій.

Якщо провести аналіз діаграми розсіювання, то помилка визначення оптимальної специфікації форми зв’язку між досліджуваними змінними, може бути зведена до мінімуму.

1) Лінійна модель.

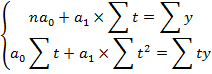
Розв’язуємо систему рівнянь для знаходження параметрів, та визначаємо , після чого розраховуємо у- , та квадрат цієї різниці. Останній показник нам необхідний для порівняння моделей, та знаходження найбільш оптимальної за умови:

Розрахункивиконаніуфайловомудокументі: Kuhii Anna Praktikum 1.xlsx.

Оскільки використовується Excel, то систему рівнянь виконуємо у матричному вигляді.

( =

По-перше, вводимо матрицю 1, розраховуємо обернену за функцією МОБР (використовуємо у кінці набір клавіш Ctrl+Shift+Enter). За допомогою функції МУМНОЖ множемо отриману обернену з матрицею 3, для знаходження параметрів.

Відповідно до заданої функції значодимо за рівнянням значення і наступні у- , та квадрат цієї різниці. Для кожної з дев’яти наданих функцій будуть певні особливості.

У своїй роботі я використовую зміну облікової ставки (на початок року) НБУ. Умовно позначено синім матрицю пов’язану з параметром t. А темно-синім обернену до неї.

Рис.2Розрахунки за моделлю 1

Рис.3 Модель 1

Бачимо, що , . Суми квадратів відхилень дорівнює 96,22.

2) Логарифмічна. Функція

Замість суми tшукаємо суму lnt.

Рис.4Розрахунки за моделлю 2

Рис.5 Модель 2

Бачимо, що , . Суми квадратів відхилень дорівнює 96,24, що є більшим значенням ніж за лінійної моделі.

3) Гіперболічна. Функція

Замість суми t шукаэмо суму 1/t.

Рис.6Розрахунки за моделлю 3

Рис.7 Модель 3

Бачимо, що , . Суми квадратів відхилень дорівнює 96,28, що є більшим значенням ніж за лінійної моделі та логарифмічної моделі.

4) Показникова. Функція

На початку ми логарифмуэмо обидві частини рівняння. Знаходимо параметри та . Експоненсіюємо (функція EXP).

Рис.8Розрахунки за моделлю 4

Рис.9 Модель 4

Бачимо, що , . Суми квадратів відхилень дорівнює 99,14, що є більшим значенням ніж за лінійної моделі та логарифмічної моделі.

5) Степенева. Функція

Ми логарифмуэмо обидві частини рівняння. Знаходимо параметр та . Експоненсіюємо параметр (функція EXP).

Рис.10Розрахунки за моделлю 5

Рис.11 Модель 5

Бачимо, що , . Суми квадратів відхилень дорівнює 99,176.

6-9)

Для 7-9 знаходимо обернені значення до у. Тому знаходимо замість суми у суму 1/у.

У випадку 9, перед перетворенням у на 1/у, ми у знаменнику виносимо значення Х, та скорочуємо його. Таким чином параметром з Х буде виступати не , а . Що треба буде враховувати при розрахунку матриць. Розгленемо більш детально.

6) Функція .

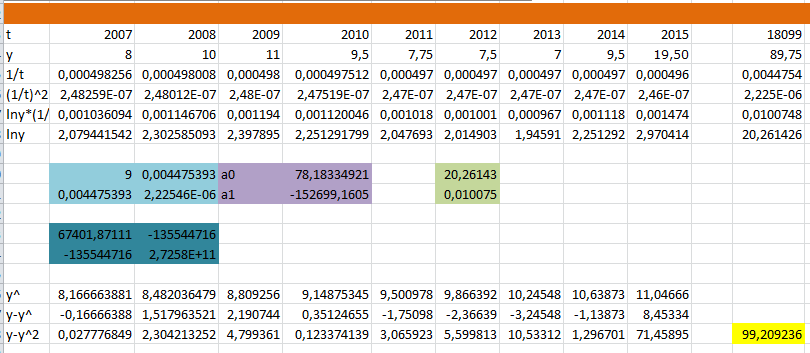
Рис.12Розрахунки за моделлю 6

Рис.13 Модель 6

Бачимо, що , . Суми квадратів відхилень дорівнює 99,209.

7) Функція

Рис.14 Розрахунки за моделлю 7

Рис.15 Модель 7

Бачимо, що , . Суми квадратів відхилень дорівнює 108,85.

8) Функція

Рис.16 Розрахунки за моделлю 8

Рис.17 Модель 8

Бачимо, що , . Суми квадратів відхилень дорівнює 108,88.

9) Функція

Після попередніх перетворень отримуємо:

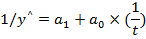
Рис.18 Розрахунки за моделлю 9

Рис.19 Модель 9

Бачимо, що , . Суми квадратів відхилень дорівнює 108,91.

Таким чином підсумовуючи усі значення квадратів відхилень ми отримаємо дані подані у табл.1.

Табл.1

Значення квадратів відхилень

	96,21805556
	96,24837957
	96,27866631
	99,14332197
	99,1763034
	99,20923607
	108,8588064
	108,8862842
	108,9137105
	96,21805556

Висновок

Попереднім дослідженням роботи була зміна золотовалютного фонду України за певний термін часу. Оскільки подібна модель виявилась залежною не тільки від часового лагу, а й інших показників, зокрема зміни облікової ставки, то для вивчення матеріалу практикума 1 було узято показник зміни облікової ставки.
Джерело використаних даних – офіційний сайт НБУ.

Згідно до опрацьованих даних та побудові моделей найбільш точно детермінує статистичні дані лінійна функція регресії. Але різниця у лінійній, логарифмічній та гіперболічній незначна, тому в подальшому можливе використання будь якого з цих методів, якщо це допоможе спрощувати розрахунок.

Дата добавления: 2015-10-28