Тема: Визначення оцінок параметрів емпіричних функцій регресії, що моделюють монотонний процес

MIHICTEPCTBO ОСВІТИ I НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

Факультет менеджменту та маркетингу

Практикум 1

З дисципліни

Економіко-математичні методи та моделі в економіці. Економетрика

На тему:

«Визначення оцінок параметрів емпіричних функцій регресії, що моделюють монотонний процес»

Студент ІІ-го курсу групи УС-31

Миколенко Владислав Вікторович

Перевірила:

Ільченко Ксенія Олександрівна

Лазаренко Ірина Сергіївна

Київ, 2015

Тема: Визначення оцінок параметрів емпіричних функцій регресії, що моделюють монотонний процес

Завданням до комп’ютерного практикуму є застосування методу найменших квадратів для поданих монотонних залежностей на прикладі моделювання динаміки росту курсу акцій:

t
Y(t)

Для цього використовуємо наступні функції регресії, які залежать від двох параметрів:

Для дослідження візьмемо приклад не росту акцій, а зміни облікової ставки.

Розглянемо трохи теорії:

економетрія — галузь економічної науки, яка вивчає методи кількісного вимірювання взаємозв’язків між економічними показниками. Отже, наведені приклади ілюструють важливість цієї дисципліни в підготовці фахівців з економіки.

Економетрія вивчає методи оцінювання параметрів економетричних моделей, які характеризують кількісні взаємо­зв’язки між економічними показниками, а також розглядає основні напрямки застосування цих моделей в економічних дослідженнях.

Математична модель кожного об’єкта (процесу, явища) містить у собі три групи елементів: 1) характеристику об’єкта, який потрібно визначити (невідомі величини), — вектор Y = (y_j); 2) характеристики зовнішніх (щодо модельованого об’єкта) умов, які змінюються, — вектор X = (x_j); 3) сукупність внутрішніх параметрів об’єкта — A.

Множини умов та параметрів X і A можуть розглядатись як екзогенні величини (тобто такі, які визначаються поза рамками моделі), а величини, що належать вектору Y, — як ендогенні (тобто такі, які визначаються за допомогою моделі).

Математичну модель можнатлумачити як особливийперетворювачзовнішніх умов об’єкта X (входу) на характеристики об’єкта Y (виходу), якімають бути знайдені.

У статистиці використовують такі методи оцінювання параметрів як:

1. Метод моментів.

2. Метод максимальної вірогідності.

3. Метод найменших квадратів.

ЗадачеюМНК є оцінка закономірностей, які спостерігаються на тлі випадкових коливань, та її використання для подальших розрахунків, зокрема, для прогнозів.

Візьмемо певний графік (рис.1)

Рис.1 Проста модель регресії

Як бачимо з Рис.1 існують відхилення як додатні так і від’ємні у залежності від того, по яку сторону від лінії лежить конкретна точка. Для однозначно’ визначеності прямої (яких може бути безліч) використовують показник розсіювання – дисперсію.

Дисперсія – це міра розсіювання (відхилення від середнього) значень випадкової величини відносно її математичного сподівання.

Якщо усі відхилення піднести до квадрату і скласти, то результат буде безпосередньо залежити від розкиду точок біля шуканої прямої. Після чого з усіх можливих прямих будк обрана така, для якої міра розсіювання досліджуваних точок була мінімальна. Тобто метод найменших квадратів заснован на вимозі мінімізації суми квадратів відхилень.

У математичному виразі, принцип найменших квадратів відхилень полягає в знаходженні таких 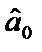і 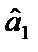, для яких найменша. Необхідна умова для цього — перетворення на нуль похідних цієї функції за кожним із параметрів 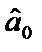і 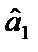. Метод, який реалізує принцип найменших квадратів, називається методом найменших квадратів (1МНК). Оскільки

,то

Виконавшиелементарніперетворення, дістанемо систему рівнянь

Оцінки параметрів моделі:

Дата добавления: 2015-10-28