Первая часть эксперимента.

Экспериментальная часть.

Классическая модель металлов Друде.

Теоретические и экспериментальные данные.

Образец – медная проволока с изоляционным слоем. При подключении образца к РИЭ мы измерили сопротивление при изменении температуры образца а также достигли температуры его плавления. Диаметр проволоки находили после удаления слоя изоляции.

Результаты опытов занесены в Таблицу 1.

Таблица 1 – эксперементальныйе и расчетные данные.

d*10^-^3м	l, м	S*10^-^9, м	R, Ом	Z	ρ, г/см^3	А, г/моль	Тпл, °К
0,1	0,50	7,85	1,41		8,96

Формулы, используемые в расчетах:

Удельного сопротивления образца известных геометрических размеров:

ρ ₀=(R·S)/l

σ=1/ ρ ₀ статической электропроводности

Концентрации электронов в 1см³ металла:

N_v= ρ_vN_A/A

n_v=N_vz

Среднего межатомного расстояния <d>:

<d>=(3)^1/3/(N_v)^1/3

Времени релаксации:

τ=(m_e)/(ρ₀e²n_v)

Длины свободного пробега электрона l:

<V>= (3kT/m_e)^1/2;

l=<V>· τ

Подвижности носителей заряда:

μ=eτ/m_e;

Напряженности электрического поля и предельной плотности тока:

Е_max= ј_max /σ₀

ј_max=U/ ρ ₀·l; ( 8.1)

Диэлектрической проницаемости металла:

ε_{r Me}=τ σ₀/ε₀(1+ω²τ²)

Коэффициента преломления:

n= (ε_r·μ_r)^1/2

Коэффициента Холла:

R_н=-1/en_v;

Оборудование

Используемый образец – медная проволока длинной 0,50м и диаметром 0,10мм покрытая изоляционным слоем.

Универсальный вольтметр В7-27 использовался для определения сопротивления образца. При измерении сопротивления образца при комнатной температуре предел измерения прибора составлял 1 Ом.

Схема для первой части эксперимента:

Рисунок 1 – схема первой части эксперимента.

Рисунок 2 - схема для второй части эксперимента.

Первая часть эксперимента.

Первая часть эксперимента проходила при температуре Т=20ºС и пределе измерения прибора 1Ом. Сопротивление проводника определили экспериментально (R=1.41 Ом). Тогда рассчитаем: 1) удельное сопротивление нашего образца; 2)количество атомов металла в 1 см³; 3)концентрацию электронов; 4)среднее межатомное расстояние; 5)время релаксации; 6)длину свободного пробега электрона; 7)диэлектрическую проницаемость металла; 8)его коэффициент преломления; 9)напряженность электрического поля и предельную плотность тока(8); 10)подвижность носителей заряда; 11)коэффициент Холла; 12)дрейфовую скорость по формуле V_др = j/en_v:

1)

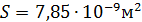
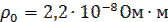
2)

3)

4)

5)

6)

Для того, чтобы определить диэлектрическую проницаемость металла найдем частоту ω~ τ^-1, при которой у металла появляется «реактивный» характер:

7)

8)

9)

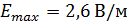
10)

11)

12)

Для модели металлов Зоммерфельда скорость на поверхности Ферми считается как типичная скорость электрона (v_F = (ħ/m)k_F; k_F = (3π²n)^1/3 ).

Найдем энергию и импульс Ферми

E_F=(ħm) ²/2m P_F=ħ* k_F

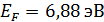
Дата добавления: 2015-10-28