Розгорнутий алгоритм для знаходження оберненої матриці

Нехай дано:

Прямий хід (алгоритм утворення нулів під головною діагоналлю)

Поділимо перший рядок матриці А на отримаємо:, j – стовпець матриці А.

· Повторюємо дії для матриці I, за формулою: , s – стовпець матриці I

Отримаємо:

· Будемо утворювати 0 у першому стовбці:.

· Повторюємо дії для матриці І, за формулами: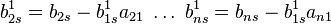

Отримаємо:

· Продовжуємо виконувати анологічні операції використовуючи формули:

при умові, що

· Повторюємо дії для матриці І, за формулами:

при умові, що
Отримаємо:

Зворотній хід (алгоритм утворення нулів над головною діагоналлю)

Використаємо формулу: , при умові, що
Повторюємо дії для матриці І, за формулою :, при умові, що

Остаточно отримуємо:

Приклад

Розв'яжемо систему рівнянь:

Запишемо її у вигляді матриці 3×4, де останній стовпчик є вільним членом:

Виконаємо такі дії:

· До рядка 2 додамо: -4 * рядок 1.

· До рядка 3 додамо: -9 * рядок 1.

Отримаємо:

· До рядка 3 додамо: -3 * рядок 2.

· Рядок 2 ділимо на -2

· До рядка 1 додамо: -1 * рядок 3.

· До рядка 2 додамо: -3/2 * рядок 3.

· До рядка 1 додамо: -1 * рядок 2.

У правому стовпчику отримаємо рішення:

.

Розв’язування прикладів

1. Для матриці A знайти обернену матрицю.

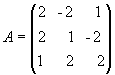
Рішення. Знаходимо спочатку детермінант матриці А:

Це означає, що обернена матриця існує і ми її можемо знайти по формулі , де А_{i j} (i,j=1,2,3) - алгебраїчні доповнення до елементів а_{i j} початкової матриці.

звідки

.

2. Знайти матрицю, обернену до матриці.

A =

Знаходимо спочатку визначник матриці A:

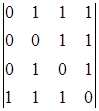= = 1 (-1)⁴⁺¹ 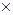= (-1) =

= (-1) 1 (-1)³⁺¹ = -1 0. Отже обернена матриця існує.

Знаходимо алгебраїчні доповнення:

A₁₁=(-1)¹⁺¹ = 2 A₂₁=(-1)²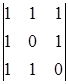⁺¹ = -1

A₃₁=(-1)³⁺¹ = -1 A₄₁=(-1)⁴⁺¹ = -1

A₁₂=(-1)¹⁺² 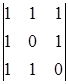= -1 A₂₂=(-1)²⁺² 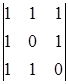= 1

A₃₂=(-1)³⁺² = 0 A₄₂=(-1)⁴⁺² = 0

A₁₃=(-1)¹⁺³ 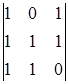= -1 A₂₃=(-1)²⁺³ = 0

A₃₃=(-1)³⁺³ 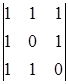= 1 A₄₃=(-1)⁴⁺³ = 0

A₁₄=(-1)¹⁺⁴ = -1 A₂₄=(-1)²⁺⁴ = 0

A₃₄=(-1)³⁺⁴ = 0 A₄₄=(-1)⁴⁺⁴ 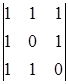= 1

Підставляючи у формулу (3) знайдені значення, одержуємо:

A^-1 =

Перевірка. Одержаний результат можна легко перевірити.

Оскільки, AA^-1 = E, де E –це одинична матриця, то:

A 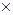A^-1 = =

=

=

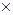
Отже, обернену матрицю знайдено вірно.

Висновки

Мета моєї курсової роботи – дослідження матеріалу по оберненим матрицям, на основі якого, складається обчислення оберненої матриці до заданої.

В процесі її написання я зібрав, опрацював і переосмислив літературні джерела. Свої дослідження я починав з пошуку матеріалу про матриці, та обернені матриці.

Отже, висвітливши основні поняття обернених матриць, можна прийти до висновку, що процес знаходження обернених матриць за допомогою формули є швидким і простим методом аналізу стану певного об’єкта.

Проаналізувавши літературу та інші джерела з даної теми, були сформульовані основні означення щодо обернених матриць. Було визначено і розкрито зміст основних методів знаходження обернених матриць.

Показавши їх практичне застосування, було доведено, що всі розглядувані методи є ефективними для знаходження матриці оберненої до даної.

Найбільш зручним виявився метод Гауса — Йордана, так як він є універсальним, так як за допомогою цього методу можна розв'язати систему лінійних алгебраїчних рівнянь, знайти обернену матрицю, знайти координати вектора у заданому базисі, відшукати ранг матриці.

В результаті виконання курсової роботи були систематизовані знання щодо обернених матриць та основних методів їх знаходження.

Загалом працювати над курсовою роботою про обернені матриці мені сподобалось.

Можу ще додати, що уже не одне століття вчені займаються дослідженнями способів знаходження обернених матриць і будемо сподіватись, що ця галузь буде розвиватись і надалі. І хто знає, може в майбутньому хтось із нас зможе зробити свій внесок в розвиток застосуваня обернених матриць, адже шанс є у кожного! Успіху вам.

Дата добавления: 2015-10-28