Способи знаходження обернених матриць

Теорема 3. Для того щоб існувала матриця, обернена до матриці А, необхідно й достатньо, щоб матриця А була невиродженою.

Необхідність. Припустимо, що для матриці А існує обернена матриця А^-1. Тоді А?=Е. Звідси, за теоремою про множення визначників 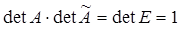, тобто . Тому , і, отже, матриця А — невироджена.

Достатність. Нехай матриця А — невироджена. Тоді, як випли­ває з рівностей (2), матриця

є оберненою до матриці А.

Матрицю, обернену до матриці А, позначають символом А^-1. Доведемо, що для будь-якої невиродженої матриці А існує тільки одна обернена матриця А^-1. Справді, якщо матриця С така, що АС = СА = Е, то

САА^-1 = (СA)А^-1 = ЕА^-1= А^-1,

САА^-1 = С(AА^-1) = CЕ= C,

і отже, С=А^-1. Таким чином, для кожної невиродженої матриці A=(a_ik) існує, і притому тільки одна, обернена матриця

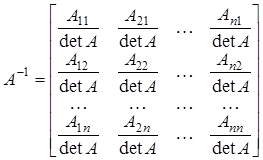(3)

Співвідношення (3) називають формулою оберненої матриці. Якщо матриця А невироджена, то обернена до неї матриця А^-1 також невироджена. Справді, з рівності АА^-1=Е і теореми про множення визначників випливає, що 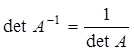; тому матриця А^-1 також невироджена. Оберненою до матриці А^-1, очевидно, є матриця А.

Застосування обернених матриць до розв’язування прикладів

Знаходження оберненої матриці є важливою складовою в розділі лінійної алгебри. З допомогою таких матриць, якщо вони існують, можна швидко знайти розв'язок системи лінійних рівнянь. Розглянемо метод Гауса — Йордана, який використовується для розв'язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Гауса. Названий на честь Гауса та німецького математика та геодезиста Вільгельма Йордана.

Алгоритм

1. Обирається перша зліва колонка, що містить хоч одне ненульове значення.

2. Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.

3. Усі елементи першого рядка діляться на верхній елемент обраної колонки.

4. Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.

5. Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.

6. Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.

7. Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.

8. Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).

Дата добавления: 2015-10-28